基于改进持支向量机的猪肉价格预测研究

姜百臣，冯凯杰，彭思喜

（华南农业大学经济管理学院，广东 广州 510642）

中国是猪肉消费大国，猪肉占消费肉类的年均消费量（2000—2015年）为64.70%，是居民摄取动物蛋白的最重要来源，在中国始终具有不可替代性；但是，随着城市与农村消费结构的剧烈变化，“价高伤民，价贱伤农”的“猪周期”现象频现，对稳定社会经济和人民生活产生较大的不利影响。因此，在“猪周期”中做出准确的价格预测，对于猪肉产业合理安排生产、销售等前端生产活动和居民进行合理消费决策具有重要的指导意义和参考价值。

国内外对猪肉和其他农畜产品价格波动及常用的研究主要有两类：一是价格波动机制研究。孙红英等［1］以改进的投入产出价格影响模型测算发现猪肉价格波动对CPI篮子商品具有很强的带动性。李俊青［2］运用Minot福利模型研究生猪养殖的粮食投入通过影响生猪供给量从而影响散养户的生产福利。郭利京等［3］应用市场微观结构理论分析生猪价格波动的原因，证实信息缺失和从众行为是造成生猪周期性供求失衡的主要原因。王俊能等［4］采用EMD 和FFT 方法对中国的生猪产量波动周期进行分析，发现我国生猪产量变化率存在多尺度波动周期，但EMD方法对数据样本长度要求高，容易产生模糊结果。梁俊芬等［5］运用CensusX12季节调整法和H-P滤波法研究生猪价格波动，显示生猪价格长期呈非线性缓慢上升趋势，受外部随机因素冲击较大。

二是价格预测研究方法。（1）计量统计和单一预测模型。Qu Hongquan等［6］通过M2与生猪产量的年增率对猪肉价格进行简单的线性回归预测；邱俊杰等［7］利用2009年4～5月猪肉价格日度数据构建自回归移动平均（ARMA）模型对中国猪肉价格进行短期预测；谷国玲等［8］通过改GM（ 1，1）模型的背景值和运用M次累加的方法进行残差校正，结果表明改进后GM（ 1，1）的预测值精度更高。Zhang等［9］、罗军等［10］从猪肉市场长期供求关系、周期性波动及外界因素等方面预测价格波动。周伍阳等［11］运用二次指数平滑法分析生猪价格波动周期及趋势预测。（2）智能预测模型。张维宏［12］分析了广东生猪养殖现状，并利用灰色预测模型对广东生猪出栏数量进行预测，结果显示模型预测精度合格可信，但该模型还存在对历史数据依赖的局限。平平等［13］将ANN、GM（1，1）和三次指数平滑等预测模型进行混合，并对吉林省生猪价格进行预测，结果表明组合预测比单项预测有明显的精度改进。屠星月等［14］基于农产品价格时间序列组合预测方法与RBF神经网络的集成预测模型，实现计量经济模型与智能模型方法在线性与非线性数据处理的互补效果，但RBF神经网络预测中的滞后期数会对预测结果产生影响。丁琳琳等［15］通过构建支持向量机模型对生猪价格进行预测，较好地反映生猪价格及其影响因素之间的复杂的非线性关系。Li Zhe-min等［16］提出了一种基于遗传算法的混沌神经网络模型猪肉价格的短期预测。

综合国内外研究，猪肉行情研究主要是价格波动机制及高精确预测工具两个方向，但预测模型在研究中强调样本统计特征，并没有很好地体现出价格波动内在的经济原理，加上现阶段的预测模型存在一定缺陷，导致一般预测的结果与实际有较大偏差，以目前预测性能较好的支持向量机SVM为例，则会在预测过程中容易出现拐点及滞后问题。为此，本研究引入EEMD分解方法剖析“猪周期”价格波动原理，并结合遗传算法（GA）优化的支持向量机（SVM）预测模型EEMD-GA-SVM，为生产者与消费者提供理论依据和具有价值参考的实用预测工具，有助于防范猪价波动的周期风险。

1 材料与方法

1.1 数据来源

采用2002年1月至2017年12月中华人民共和国农业部畜牧业司官网（http://www.xmys.moa.gov.cn/）猪肉数据作为样本数据建模。

1.2 集成经验模态分解（EEMD）方法

EEMD的一般步骤：（1）在原始信号中加入均值为0，标准差0.1～0.4倍的白噪声。（2）找出原信号x（t）的所有极值点，然后通过三次样条函数拟合出极大值包络线 e+（t）和极小值包络线 e-（t）构成一条均值包络线m1（t）:

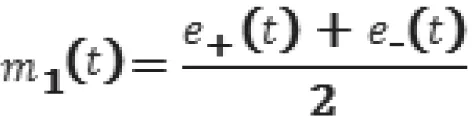
将原信号序列减去m1（t）得到一个去掉低频的新信号（t）：

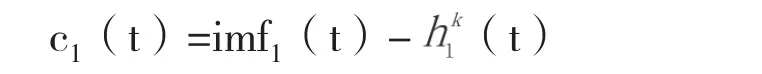
用原信号x（t）减去c1（t），得到一个去掉高频成分的新信号r1（t）:

（4）对r1（t）重复上述得到c1（t）的过程，得到第二个IMF分量c2（t），如此反复，直到第n阶IMF分量cn（t）或其余量rn（t）小于预设值，EMD分解过程终止。最后：

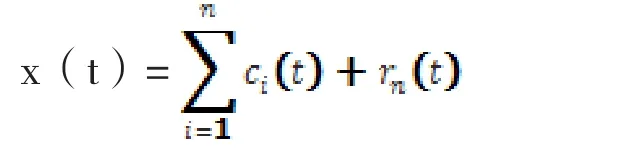
式中，rn（t）为趋势项，x（t）为n个频率从高到低的本征模态函数 IMF。

（5）分别对原始信号加入不同的白噪声，重复步骤（2）至步骤（4）。

（6）不断重复以上流程N次，对次分解结果进行集成平均，视作最后的分解结果。利用统计方法控制加入的白噪声:

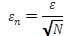
1.3 支持向量机回归基本原理

SVM回归思路：首先从最优超平面出发，给定训练集样本 {（x1，y1），…（xn，yn）}，xiR，yi（+1，-1），在线性可分条件下得到：

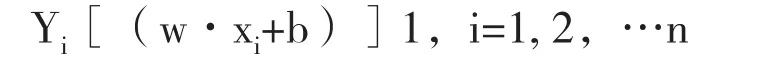
式中，ω为超平面的权值向量;b为偏置项。

在线性不可分条件下，需要引入松弛变量ζi，加入松弛变量后的线性规划问题表现形式为：

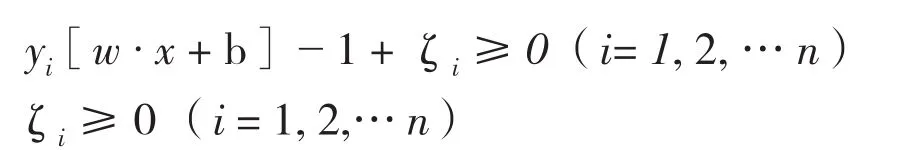
寻求目标函数变为：

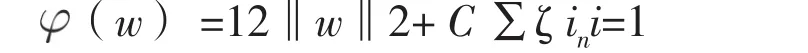
其中C为惩罚因子，用于权衡式（2.13）中的ζi值，避免因太大而降低解的质量。

利用拉格朗日乘子将上式转化为对偶形式并求解，得到SVM决策函数:

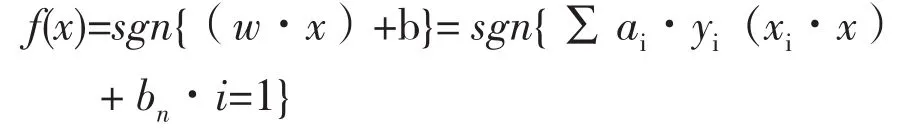
式中，ai为拉格朗日乘子。

如果核函数k（xi，xj）能够满足Mercer条件，那么空间内积高维运算非线性问题就可以解决。对应的分类决策函数表示为：

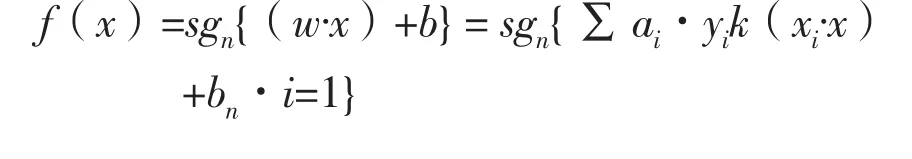
式中，核函数k（xi，xj）为径向基函数（RBF），是较常用的核函数:

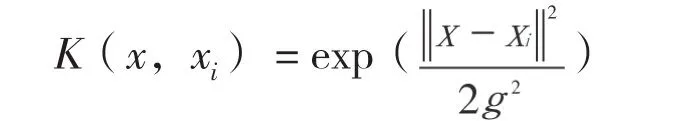
式中，g为核参数且g＞0。

1.4 支持向量机的改进

一般在基于RBF核函数的SVM算法中，惩罚系数C和核函数参数g分别刻画的是对错分样本惩罚程度、支持向量之间的相关程度，前者决定了算法的鲁棒，后者决定了算法的泛化能力；损失函数P的选取对SVM模型计算精度有很大影响，为进一步提升SVM的预测性能，本研究的参数寻优组合为（C，g，p）。

1.5 遗传算法原理

遗传算法（GA）是Holland 教授于1975年提出的一种优化方法。本研究选用谢菲尔德大学Matlab遗传工具箱，该工具箱编程相对灵活，功能齐全，应用遗传算法优化支持向量机的主要步骤如下：

（1）编码：将问题的解以适合于遗传算法的表示，在交叉、变异等操作之前需进行，本研究选用最简单的二进制编码。

（2）初始化种群：按照设定规则生成一定数量的个体作为初始种群，由随机生成的（C，g，p）组成。

（3）选定目标函数对初始种群进行回归训练，将训练结果的均方误差作为目标函数值，并计算每个个体的适应度值。

（4）根据设定概率，在二进制编码的条件下，对初始种群进行选择、交叉、变异操作分别为轮盘赌选择、单点交叉及二进制变异，进而得到新一代种群（C，g，p），并对新一代种群进行SVM回归训练。

（5）如果种群满足终止规则，输出适应值最优的个体作为最优参数参与建模，进行回归预测；则返回步骤（3），增加进化代数或减小适应度精度继续参与运算，直到满足条件，运算终止。

1.6 预测流程

有效分析猪肉价格的波动规律和捕捉到有用的价格信息是进行有效预测的重要前提，本研究构建基于改进支持向量机预测主要包括3个流程（图1）：（1）通过EEMD方法分解出总数为T猪肉价格的样本，获得分量的平均周期作为“猪周期”L的参考依据。（2）前T-L个样本猪肉价格作为输出变量，前T-L玉米、豆粕和仔猪价格等作为训练样本输入，获得最优的（C，g，p）参数组合，进行下一步预测。（3）以改进的SVM对输入最后的L个玉米、豆粕和仔猪价格进行预测，得出最终L个猪肉价格预测值。

图1 猪肉价格预测流程

1.7 评价指标

采用学术研究中常用的3个综合性预测评价指标，描述预测值与真实值之间平均误差情况，能够清晰反映预测值与真实值拟合度。各评价值结果越小，表明该预测模型精度越高。

（1）均方根误差RMSE（Root Mean Squared Error），表示各数据偏离真实值的距离平方和的平均数开方观测真实值与预测值的偏差。

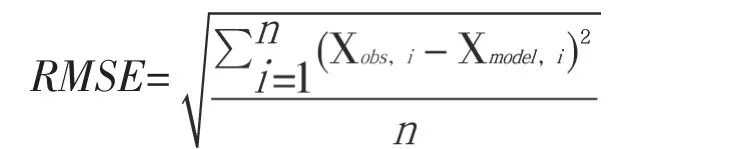
式中，Xobs为真实值，Xmodel为模型预测值。

（2）绝对误差平均MAE（ Mean Absolute Error），表示所有单个观测值与算术平均值的偏差绝对值的平均。

（3）Theil 不等系数，反映预测值与真实值的拟合程度，当等于0时，表示完全拟合;当等于1时，表示完全不能拟合。

2 实证检验结果与分析

2.1 EEMD分解结果分析

首先利用MATLAB的EEMD程序对180个猪肉价格数据样本进行集成模态分解，最后获得本征模函数IMF1～IMF6及趋势项res（图2）。

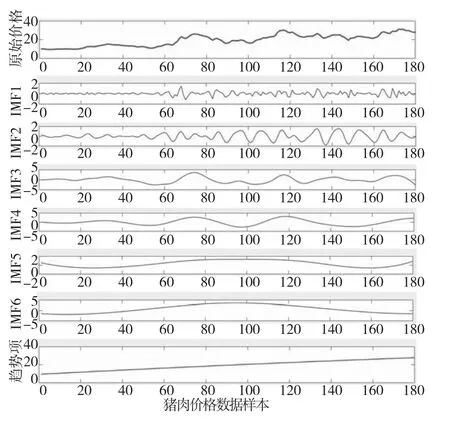
图2 猪肉价格EEMD分解的IMF分量

（1）高频分量IMF1～IMF3：高频分量反映的是短期供给均衡导致价格波动，具有频率大、噪声高的特点，刻画出短期价格波动的强度与持续时间，有助于养殖户。其前段的猪肉价格分量较后段的价格分量平稳，也印证2008年后期供求失衡的情况出现的频率较高，反映了猪价一轮下跌下一波暴涨的市场预期，长期以往对国内肉食市场的健康发展带来不利影响。

（2）低频分量IMF4～IMF6：低频分量反映了“猪周期”重大事件的影响，国内的政策变化、疫病等都对猪肉价格产生较大的影响，也是推动猪肉价格趋势成形的主因。由于政策变化、人工成本、饲料价格对整个养殖产业链持续且深刻的影响，直接影响生猪产量的起伏变化，例如，2006年的“蓝耳病”、2014年中美关于猪肉的贸易摩擦，都对猪价产生较大的冲击。

（3）趋势项RES：长期价格趋势是上涨的，猪肉是CPI上涨的原动力，反映出近几年国内高通胀的势头与猪价是同步发生的。随着未来发展规模化与家庭养殖精致化，整个肉猪产业链将会完善，养殖业高质量的发展是未来的大趋势，也是保证猪肉价格合理性的关键。

透过EEMD分解的猪肉价格分量，以及猪肉价格的时间多尺度信息，包含“猪周期”的空间结构，基本反映了“母猪怀孕－产仔-育肥-市场销售”的价格周期。

2.2 “猪周期”判断

通过对EEMD分解结果进行分析，可以看到EEMD的IMF分量能较好地对应时间多尺度特征，既猪肉价格在不同运动周期的细致规律。对同频率的分量取其波动的平均周期对应出“猪周期”，即高频分量IMF1～IMF3的平均波动周期，以及低频分量IMF4～IMF6的平均波动周期（图3），由于趋势项是一个完整的趋势，是平滑的上升曲线，并不具有周期性。因此，本研究选择高低分量与低频分量的平均波动周期作为预测长度的标准。

图3 高频分量与低频分量的平均波动周期

通过对频率分量的谷峰、谷底的进行统计，分别获得的波动周期分别是6个月的短“猪周期”L1，以及 20个月的长“猪周期”L2。明显地，6个月的波动周期L1符合一般的生猪养殖到成品销售的完整流程；而20个月表示的是考虑到政策变化、疫病的一个价格波动周期。因此，本研究的预测周期从短“猪周期”L1和长“猪周期”L2的基础上进行价格预测。

2.3 EEMD-GA-SVM预测

利用MATLAB软件的LIBSVM支持向量机回归模型结合遗传算法GA进行训练和预测，利用EEMD分解获得的高频分量、低频分量、res趋势项输入数据进行模型训练，构建出一个EEMD-GA-SVM模型。同时，为更精准反映出EEMD-GA-SVM模型的精准性和适用性，与GS-AVM、PSO-SVM、BP神经网络和ARIMA等常用预测模型进行横向对比，分别预测6个月度（2017年7～12月）的价格走势，以及在长 “猪周期”20个月度（2016年4月～2017年12月）的价格走势。

对2017年1～12月的价格进行预测，通过预测值和实际值之间平均绝对百分比误差和均方根误差等指标比较，结果显示:

（1）EEMD-GA-SVM的预测性能表现最佳。从表1可以看出，神经网络BP-ANN在预测周期6个月时RMSE为1.99，在预测周期20个月时RMSE为2.97，其他两个指标对比有明显差异，说明BP-ANN训练过程中出现了过学习的问题，无法很好地还原不同“猪”周期的运动规律；ARIMA模型RMSE和Theil系数偏差较大，对处理非线性的猪肉价格欠缺敏锐性，局限性明显；而SVM的3个预测指标与BPANN的误差偏离度差距不大，也印证过往农产品价格研究中SVM模型存在拐点滞后的问题。

而EEMD-GA-SVM很好地克服其他模型的局限，整体预测精度较原生SVM和神经网络BP-ANN精度有较大提升，预测周期无论是6个月或20个月，其预测结果均达到较高置信水平，整体预测效果明显优于BP-ANN和ARIMA，反映出其泛化能力增强，预测误差小，鲁棒性强。因此，印证GA优化的SVM模型结合EEMD方法预测生猪价格更可靠及适用性。

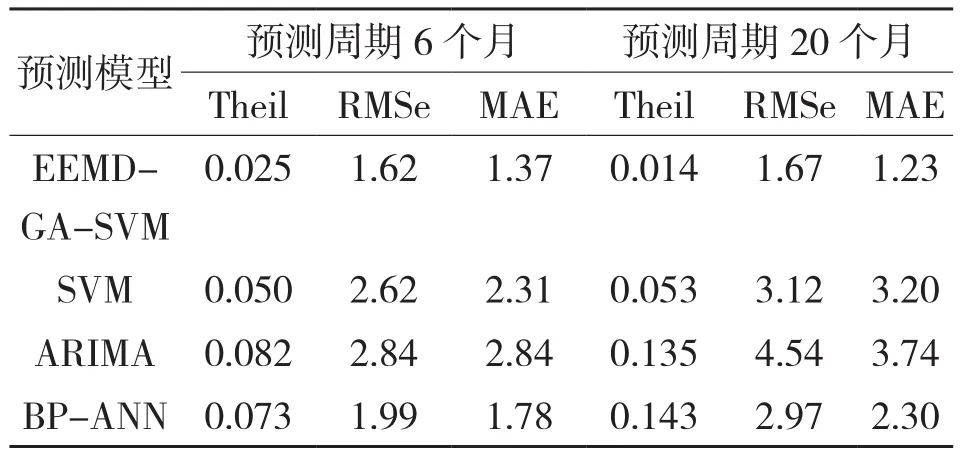
表1 猪肉集贸市场价格预测效果评价指标比较

（2）EEMD-GA-SVM能够更清晰还原猪肉价格内在波动规律。如图4和图5所示，6个月的短“猪周期”预测精度更精确，贴合猪肉真实的波动规律。短“猪”周期主要体现当养殖户发现短期意外事件所导致的生猪行情转变的反应，样本数据表现出更强的非线性 ，而EEMD-GA-SVM模型能更为灵敏地捕捉到猪价短期波动特征。“长”猪周期为多个“短”猪周期编织而成的“价格蛛网”，响应的时间跨度相对滞后，导致预测精度相对下沉，从以上4个预测模型的预测指标结果——长期预测精度逊于短期预期精度，反映的是经济效应在时间与市场反应之间的错配，而与训练样本的数据量并不直接预测精度。

图4 各个模型预测结果与真实值对比（预测周期6个月）

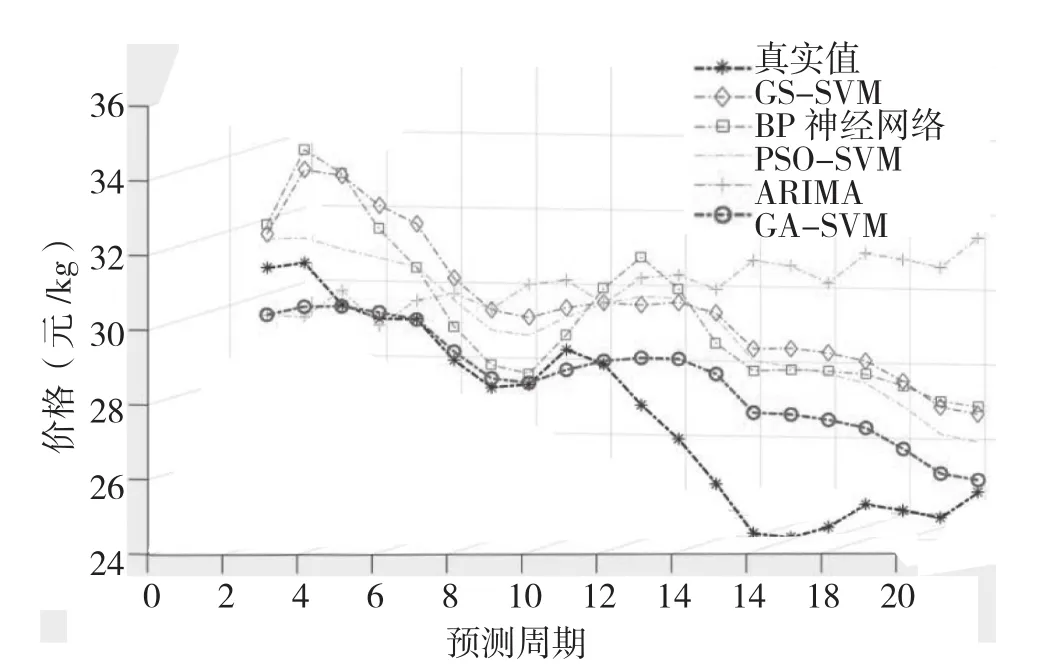
图5 各个模型预测结果与真实值对比（预测周期20个月）

3 结论与启示

本研究尝试引入EEMD方法对“猪周期”进行剖析理解，并运用GA方法全方位优化SVM以提升预测结果的稳定性和实用性，依据实证结果得到以下结论及启示：

（1）根据EEMD方法挖掘出的“猪周期”具有实际经济意义，能挖掘出“猪周期”真实的内在波动特征，并结合遗传算法改进的支持向量模型对猪肉价格预测更为精准，深刻还原出猪肉价格波动的动态演变机制，具有较高的参考指导价值。

（2）生猪价格的影响因素众多，且具有动态性，随着时间的变化，这些影响因素的贡献率可能发生变化，还可能出现新的影响因素。根据本研究结论，对于6个月的短“猪周期”的判断及价格预测，相关部门在信息监控预警调控调配更多资源，提高与养殖户的合作力度，适时指导养殖户调整生猪育肥周期。

（3）应对20个月的长“猪周期”，由于历史价格对未来价格有一定滞后性影响，建议政府部门将生猪价格指数保险融入政策性农业保险巨灾风险准备金体系，从而分散和转移由宏观经济波动引起的长期性风险。

（4）通过运用GA方法全方位优化SVM的EEMD方法为基础，可以建立足够灵敏和稳定的预警机制，有助于相关政府部门做出相关调控决策。