从定积分的角度看粗糙集

刘士虎

(云南民族大学 数学与计算机科学学院，云南 昆明 650504)

粗糙集(rough sets)理论[1]是波兰数学家Pawlak于1982年提出的一种数据分析理论，它是一种全新的处理模糊和不确定知识的数学工具.其主要思想就是在保持分类能力不变的前提条件下，通过对知识的约简，导出问题的决策或分类规则[2].在学习粗糙集理论的过程中，判断一个集合是精确集还是粗糙集，其关键点在于对所构造的上、下近似集的判定：如果上近似集等于下近似集，则此集合为精确集，否则就称之为粗糙集.

在对一个函数是否可积的研究过程中，法国数学家Darboux[3-5]在给出“Darboux大和、Darboux小和”的基础上，建立了Darboux积分的概念，并实现了和黎曼积分[6]的完美对接：达布积分等价于黎曼积分，即一个函数达布可积当且仅当它是黎曼可积.

粗糙集理论中，有上近似集和下近似集这组紧密相关的概念，而且集合是否是粗糙集完全取决于所构建的上、下近似集是否相等.在定积分理论中，黎曼可积的充分必要条件就是在极限思想下，Darboux大和等于Darboux小和.这一点很有意思！基于此，本文从积分的角度，对照粗糙集的定义和基本性质，给出一种全新的描述.

1 预备知识

为了在后文叙述方便，下面先给出一些用到的基本概念及其数学表达式(详细内容请参阅文献[2,6]).

定义1 给定知识库K=(U,R)，对于每个子集X⊆U和一个等价关系R∈ind(K)，定义2个子集：

(1)

分别称他们为X的R下近似集和R上近似集，其中R为U上的一个等价关系.

定理1 对于给定的知识库K=(U,R)，子集X⊆U和一个等价关系R∈ind(K)，下面结论成立：

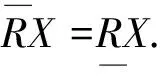
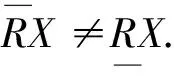
从近似的定义，可以直接得到R下近似集和R上近似集的下列性质：

定理2 对于给定的知识库K=(U,R)，子集X⊆U和一个等价关系R∈ind(K)，成立：

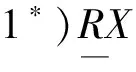
定义2 设函数f(x)在区间[a,b] 上的上确界和下确界分别为M和m，在子区间[xi-1,xi]上的上确界和下确界分别为Mi和mi.则称和式

为相应于分法P的Darboux大和，和式

为相应于分法P的Darboux小和.

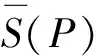
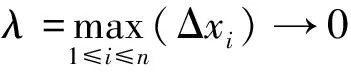
2 从积分的角度看粗糙集

在本部分，对粗糙集的定义及其性质，从积分的角度给出一定的探究.具体的工作包含如下几个层面的分析探讨.

2.1 等价关系R∈ind(K)与Darboux和中的分法P

熟知，一个集合为空集或者它的元素都是有序对，则称这个集合是一个二元关系[7].若此集合满足如下3个性质：

自反性 对于任意的x∈X，恒有(x,x)∈R;

对称性 若(x,y)∈R，则(y,x)∈R;

传递性 若(x,y)∈R且(y,z)∈R，则(x,z)∈R;

则称关系R为等价关系.

粗糙集理论中，寻求问题的决策或分类规则，其前提条件是要保持分类能力不变.简言之，此处的分类能力，指的就是给定的某个等价关系R或若干等价关系R1∪R2∪R3；保持不变，指的是对研究对象X(⊆U)而言，不管是R还是R1∪R2∪R3，其分类结果是一样的.

NSO的主要任务是管理NATO的所有标准化工作，包括制定标准化政策，协调标准化工作；制定法律法规来规范标准的制定、批准和发布工作；支持采用标准化成果，支持各任务组的标准化管理工作；制定术语政策与指南；与民用标准化组织开展合作，发布标准，开展标准化宣传等。

Darboux和中提及的分法P，指的是对于定义在区间[a,b]上的有界函数f(x)，任意给定若干个点xi∈[a,b]，把该区间分割成若干个子区间[xi-1,xi]. 不同的分法，所得到的子区间不尽相同.

等价关系R所处理的对象是待研究的问题X，处理结果是X的一系列子集，构成了一个划分.类似的，Darboux和中某个分法P对问题的处理结果，是待研究问题(即区间[a,b])的一系列子区间.显然，这是两者之间的一个共同之处.除此之外，对于等价关系R下得到的一系列子集，可以反馈于X，从中导出问题的决策或分类规则.对于分法P得到的一系列子区间[xi-1,xi]，可以进一步被用来计算所谓的Darboux大和与Darboux小和.

由上不难发现，Darboux和与等价关系R对于问题的分析，起到了异曲同工的作用.这一点，也是本文中要阐述的从积分角度看粗糙集的第一个亮点.

2.2 上下近似集合与Darboux和

对于事先给定的等价关系R，其对X⊆U做的划分如图1(a)所示.对于区间[a,b]上的有界函数f(x)，其在某个给定分法P下的示意图可以用图1(b)表示.

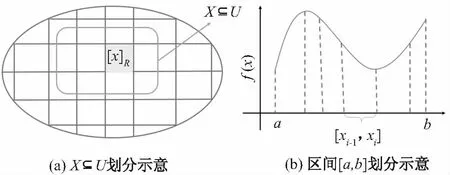
图1 关系R对X⊆U的划分示意图及分法P对区间[a, b]的划分示意图

根据(1)的表达形式，图1(a)中给定的等价关系R对X⊆U产生的上下近似集可以表示为图2所示.同理，由定义2可知，有界函数f(x)在区间[a,b]上的Darboux大和与Darboux小和可以表示为图3所示.从图2、图3不难发现以下特点：

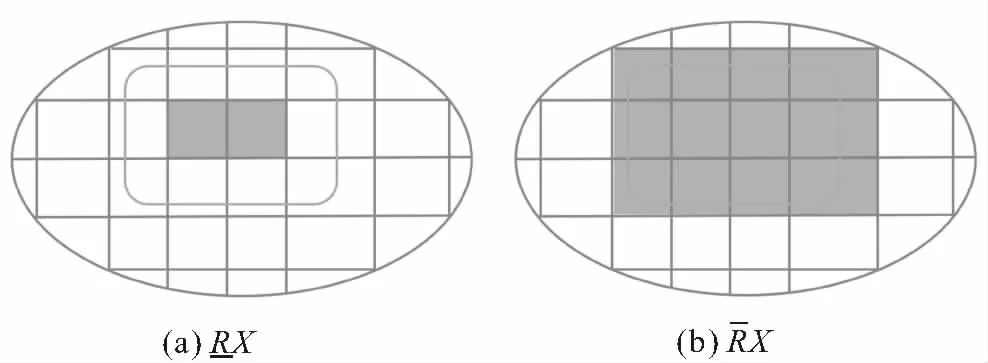
图2 关系R对U的划分关于集合X产生的上近似集集和下近似集

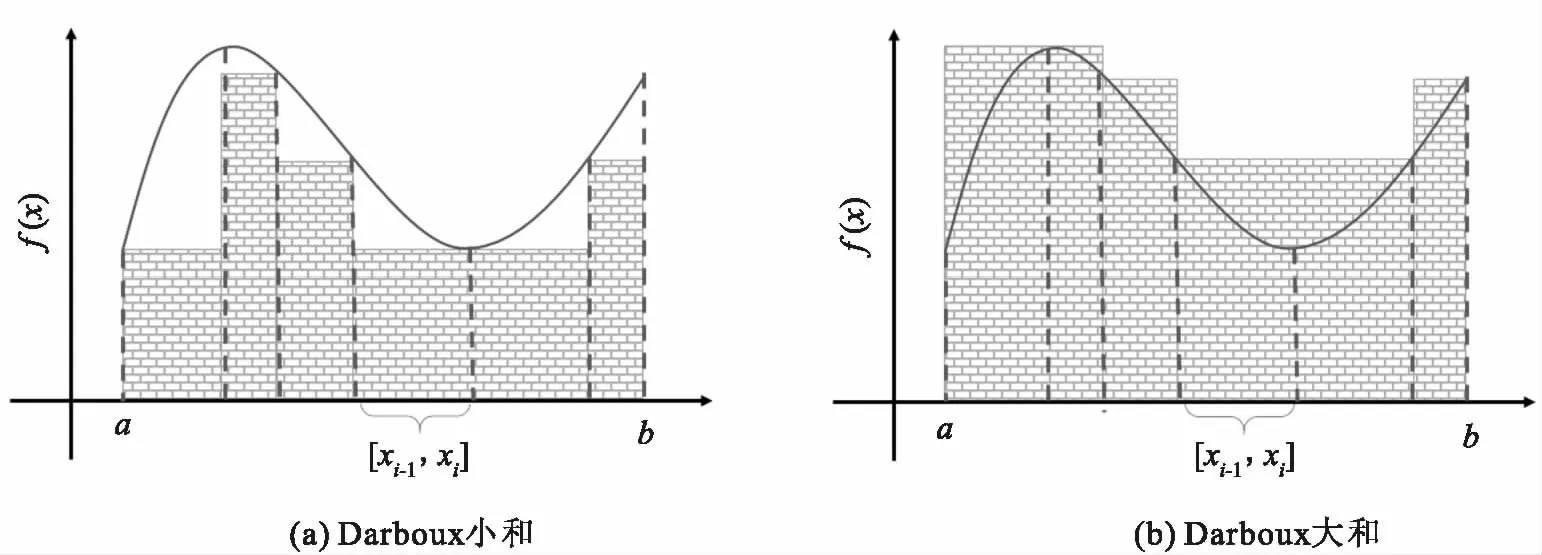
图3 有界函数f(x)在区间[a, b]上的Darboux大和与Darboux小和

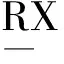
2.3 X为R精确集与有界函数f(x)在区间[a, b]上可积

由定理1可知，集合X是精确的当且仅当其在给定的某个等价关系R诱导下产生的上近似集和下近似集完全相等，即图4(a)中的阴影部分不存在.对于Darboux和而言，有界函数f(x)在区间[a,b]上可积，当且仅当在极限意义下图4(b)中阴影部分面积为0，即有界函数f(x)是Riemann可积的.

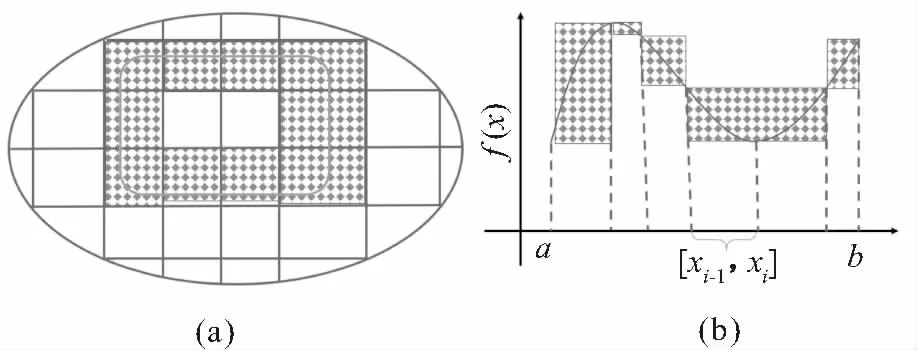
图4 集合X上下近似集的误差与Darboux和的差值对比

综上所述，在Darboux和取极限的基础上，从积分的角度而言，集合X关于等价关系R是精确集等同于有界函数f(x)是Riemann可积的.换言之，集合X关于等价关系R是粗糙集等同于有界函数f(x)是Riemann不可积的.

2.4 粗糙集性质的积分解释

在本部分，就定理2中的性质1*)～5*)，从积分的角度，对其展开一定的分析探究.对于性质6*)，本论文不对其做积分意义下的解释，性质7*)是显然的.

1)性质1*)的积分解释

对于给定的某个等价关系R，由其诱导产生的下近似集永远是原有集合X的子集，而由其诱导产生的上近似集永远以集合X作为其子集.这一点，和定理3中所描述的情况是一致的：对于任意给定的分法P，由其构成的Darboux小和永远小于函数f(x)的实际积分值，而数Darboux小和永远大于函数f(x)的实际积分值.

其实，1*)中三者之间的包含关系，和事先给定的等价关系R无关.换言之，对于任意的等价关系R而言，下近似集永远最“小”，上近似集永远最“大”.由本文第2.1部分的分析讨论可知，此性质可以看做是定理3的另外一种表达形式.

2)性质2*)的积分解释

此条性质，可以看成是性质(1*)的特殊情形，即取集合X为空集和全集U.此时，表达式⊆Φ⊆中的第一个符号“⊆”取成“=”是显而易见的，因为空集的子集只能是本身.对于表达式中的第二个符号“⊆”，由上近似的表达形式通过反证法可以任意得到其为“=”成立.从积分的角度来看，若取有界函数f(x)为零函数，即f(x)≡0，此时对于任意的分法P，恒有成立.对于2*)中表达式的积分描述，只需取有界函数f(x)为非零常值函数即可，即f(x)=C，其中C≠0.

3)性质 3*)的积分解释

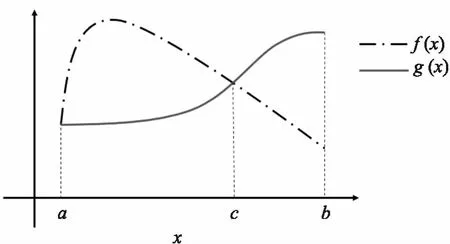
图5 有界函数f(x)、g(x)示意图

性质描述的是上近似关于“∪”运算、下近似关于“∩”运算保分配.下面我们从积分的角度对其给出描述.

给定有界函数f(x)、g(x)，且不妨假定在区间[a,b]上存在一点c∈[a,b]使得：当x∈[a,c]时f(x)≥g(x)，反之f(x)≤g(x)，具体见下图5所示.

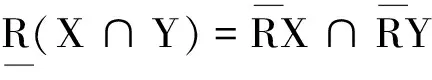
4)性质4*)的积分解释

该性质指的是对于任意的等价关系R，由其诱导产生的上近似集和下近似集保单调性.在积分意义下，此性质可以表述为.

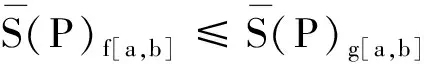
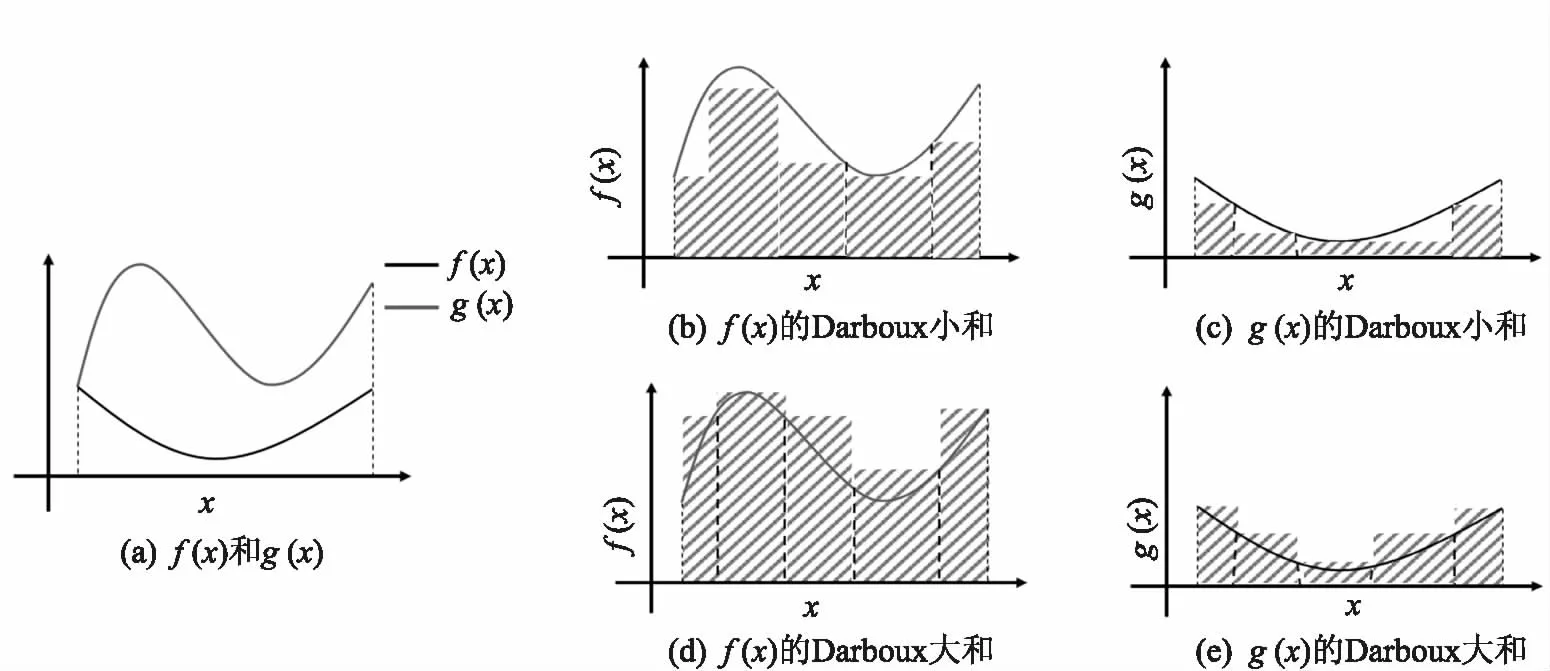
图6 f(x)、g(x)及其Darboux和(5)性质(5*)的积分解释

对于该性质的积分意义，结合上述对性质3*)和4*)的分析，显然易得，在此不再赘述.

2.5 不同等价关系下粗糙集的积分解释

由定理4可知，若对原有的分法P加入新的分点，则Darboux大和不增，小和不减.对于集合X是精确的还是粗糙的，完全取决于对其产生划分的等价关系R.换言之，在某个等价关系R1下，其是精确的，而在另外一个等价关系R2下，其完全有可能是粗糙的.下面，我们尝试对于R1⊆R2的情形，从积分的角度对其上下近似给出类似于定理4的解释.

给定等价关系R1和R2且满足条件R1=R2∪{r}，其中r为一等价关系.熟知，对于给定的集合X而言，其依赖的关系越“大”，则产生的划分越“小”，即：对于任意的x∈U，恒有[x]R1⊆[x]R2成立，见图7所示.

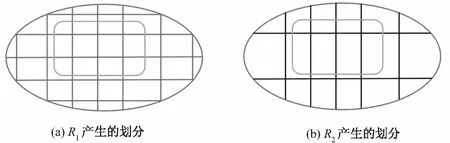
图7 等价关系R1和R2诱导下集合X的划分

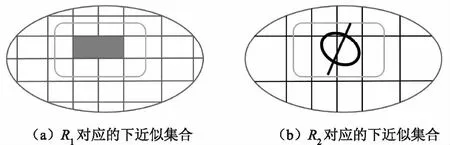
图8 等价关系R1和R2诱导下集合X的产生的下近似

关于上近似的情况，可类似得到！简言之，对于一个给定的集合X，在原有的等价关系中添加一个或若干个关系构成新的等价关系，则有以下结论：上近似集不变大，下近似集不变小.