一种结合用户相似度的社会化推荐算法

郑英丽,王 新,马 倩,解雪琴

(云南民族大学 数学与计算机科学学院,云南 昆明 650500)

为了缓解信息超载问题,以及满足现在大量的互联网用户的个性化需求,基于用户个性化的推荐算法应运而生,并且成为一个热门的研究课题.近几年来,推荐系统作为解决信息超载以及个性化推荐问题的方法之一,受到大量学者的关注和研究.推荐系统一般分为协同过滤推荐、内容过滤推荐和社会化推荐.

通常,在社交环境下,经典的协同过滤算法(CF)[1-4]是依据用户对项目的历史评分信息来预测用户的喜好,然而此算法尚未考虑用户的社交信息,推荐系统的准确率难以得到提高.一般情况下,许多社会化推荐算法通过引入用户与用户之间的相关信息来提高推荐的性能.于是,许多有趣的推荐算法被改进并提出[5-13].文献[5-7]使用矩阵分解(MF)的方法来预测用户评分.文献[5]提出概率矩阵分解(PMF)方法,该算法在非常稀疏和不平衡的数据集上表现良好.文献[6]在MF的框架下将评分矩阵中的缺失值填入其中,降低预测的误差.文献[7]在CF算法的基础上,将评分矩阵分解成2个非负矩阵,以此来预测用户的喜好,他们提出的方法在预测准确性上得到提高.文献[8-12]在MF的基础上增加用户的信任信息,使推荐准确率得到提升.文献[14]在文献[9]的基础上将推荐对象间的关联关系结合到推荐系统中,对算法做了改进,他们的算法在分类准确率上取得了更好的效果.文献[15]在推荐系统中同时引入了对象间关联关系和用户间影响力这两个因素,实验表明他们提出的方法提高了推荐准确率.文献[16]提出了一种混合型的推荐算法,将用户的信任网络和推荐项目间的属性特征结合在一起做推荐,提高了推荐精度和评分误差.值得注意的是,在文献[5-12]尚未考虑用户相似度信息,因此这成为本文研究的一个动机.

受到上述讨论的启发,考虑到目前CF算法存在的一些问题,例如数据稀疏性、冷启动和精确性.此外,用户之间的相似度信息也是影响用户评分的一个关键性因素.结合这些原因,本文主要通过结合用户间相似度和评分信息来做矩阵分解,以改善CF算法中存在的3个问题,从而提高推荐系统的预测准确性.

1 推荐算法

1.1 用户-项目评分矩阵分解

为了对评分信息进行建模,本文使用PMF方法作为推荐框架.

如表1是一个简单的用户-项目评分矩阵R,ui表示用户,vj表示项目,为了对表中的缺失值(即评分为0的值)进行预测,可以使用矩阵分解的方法,将矩阵R分解为2个低维矩阵U和V,U表示用户潜在特征矩阵,V表示项目潜在特征矩阵.

表1 用户-项目评分矩阵

如果使用3维特征矩阵来展现矩阵分解的效果,将得到分解后的U,V:

通过得到的分解后的矩阵对R中的缺失值进行预测,得到R的预测矩阵R′.

设矩阵R中有m个用户,n个推荐项目,且评分限制在[0,1]中.实际上,许多推荐系统在表示用户对项目的评分信息时都是使用从1到Rmax的整数.本文使用函数f(x) =x/Rmax将评分[1,Rmax]映射到区间[0,1]上.用户ui对项目vj的评分表示为Rij,分解得到用户相关的l-维特征矩阵表示为U∈Rl×m,项目相关的l-维特征矩阵表示为V∈Rl×n,其中列向量Ui表示用户潜在特征向量,Vj分别表示项目潜在特征向量.矩阵R的条件概率分布定义如下:

(1)

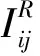
(2)

由贝叶斯推断,可以得到U和V的联合后验概率分布为:

(3)

1.2 相似性度量

相似度分析分为2类:①用户相似度度量,即度量两个用户同时感兴趣的物品数量,数目越高,相似度越高.②物品相似度度量,即对两个物品同时感兴趣的用户数量,同样的,数目越大,相似度越高.相似度的计算方法有很多,包括欧几里得方法、余弦相似度方法、Pearson相关系数方法.余弦相似度公式如下:

(4)

其中,rx,i,ry,i分别表示用户x和y对项目i的评分值.考虑到数据的稀疏性,会存在很多零值,且公式(4)计算的相似度对数值比较不敏感,容易导致结果的误差,因此本文作者采用以下改进的相似度计算公式:

(5)

下面将利用上述2个相似度公式分别对表1中给出的评分信息来计算用户之间的相似度值,结果如表2、表3所示.

表2 基于公式(4)的用户相似度矩阵

表3 基于公式(5)的用户相似度矩阵

1.3 结合用户间相似度的推荐方法(SRUS)

为了研究用户间的相关性对评分预测的影响,以及怎样利用用户相似度信息来提高推荐算法的性能,现在引入结合用户相似度的社会化推荐方法.

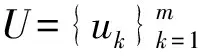
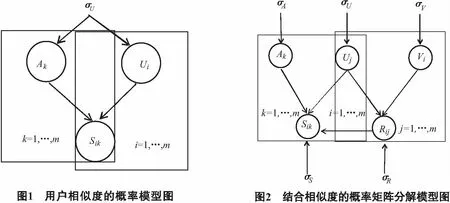
这里用户间的相似度可以通过前面介绍的相似度公式(5)进行计算.使用的概率图模型如图1所示.

通过分解相似度矩阵S,可以得到表示用户之间相关关系的低维潜在特征矩阵U和A,用户ui和uk在图G上的相似权重sik,是求解特征向量Ui和Ak的重要元素,定义S的后验概率分布为:

(6)

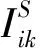
此时,结合矩阵S和矩阵R进行联合分解,对有相关关系的项目进行推荐,其概率模型如图2所示.U,V,A的联合后验概率分布表示为:

(7)

对(7)式两边取对数后可以得到:

(8)

其中C是不依赖参数的常量.

求固定参数时U,V,A的极大后验概率,等价于使下面带正则项的误差平方和函数最小化:

(9)

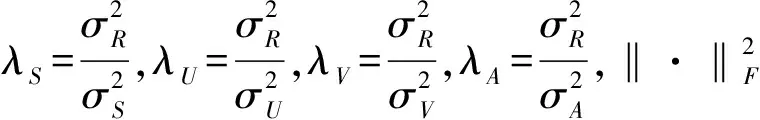
(10)

(11)

(12)

其中:g′(x)=g(x)(1-g(x))是逻辑函数g(x)的导数.

1.4 算法复杂度分析

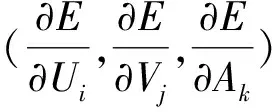
2 实验分析

通过实验对比结合用户相似度的概率矩阵分解方法(SRUS)和经典PMF方法在推荐效果上的差异.

2.1 数据集

采用movielens latest数据集,数据集相关信息如表4所示:

表4 数据集描述

2.2 评估指标

推荐系统中常用的评估指标可以分为2大类,预测准确率指标和分类准确度指标.本文采用MAE和RMSE这2个指标进行评估,它们的计算公式如下:

(13)

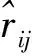
(14)

上述MAE和RMSE都是值越小,预测越准确,即推荐效果越好.

2.3 参数λS的影响

本文提出的社会化推荐算法的主要优点是结合用户相似度信息,在SRUS方法中,参数λS平衡了矩阵S和矩阵R之间的关系,当λS=0时,在矩阵分解的过程中就只考虑矩阵R的信息,当λS=inf时,只根据用户相似度来预测用户的评分,其它情况下,都是结合矩阵R和矩阵S来做评分预测的.图3给出了在特征维数l=5时,参数λS对评分预测的影响结果.

从图3可以清晰地看出当特征维数l=5时,评估指标MAE和RMSE都分别取得最小值1.025 7和1.069 3时,λS都为10.

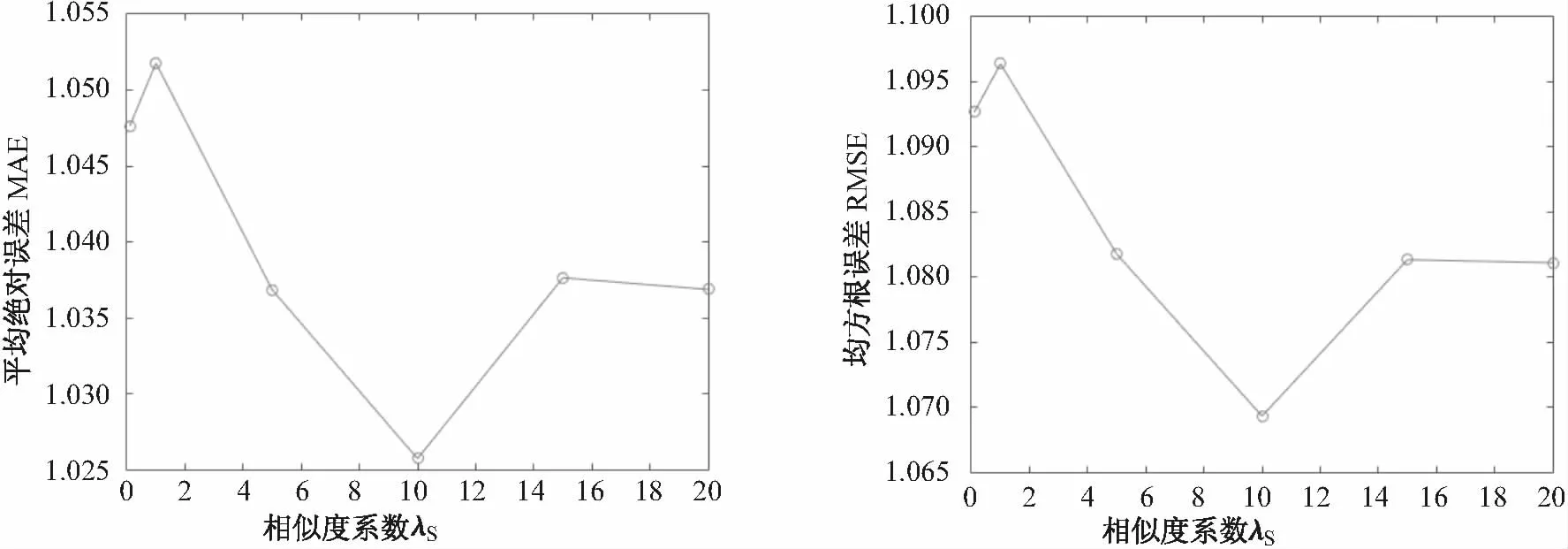
图3 实验参数λS的值对实验结果的影响(l=5)

2.4 实验结果比较

为了验证本文提出的SRUS算法在性能上的提高,与传统PMF方法作比较,由3.3节的实验结果,这里λS=10.在表5中给出了λS=10,特征维数分别为5和10的情况下的实验结果.

表5 实验结果比较(λS=10)

由表5可以得到,当特征维度l=5时,本文提出的SRUS方法较PMF方法在指标MAE上降低了1.74%,在RMSE上降低了6.20%.同样的,当l=10时,本文提出的SRUS方法较PMF方法在指标MAE上降低了5.69%,在RMSE上降低了12.12%.

同时,图4也给出了相对应的实验结果比较图,分别比较特征维数l=5(图4(a)、(b))和l=10(图4(c)、(d))情况下评估指标MAE和RMSE的变化情况.

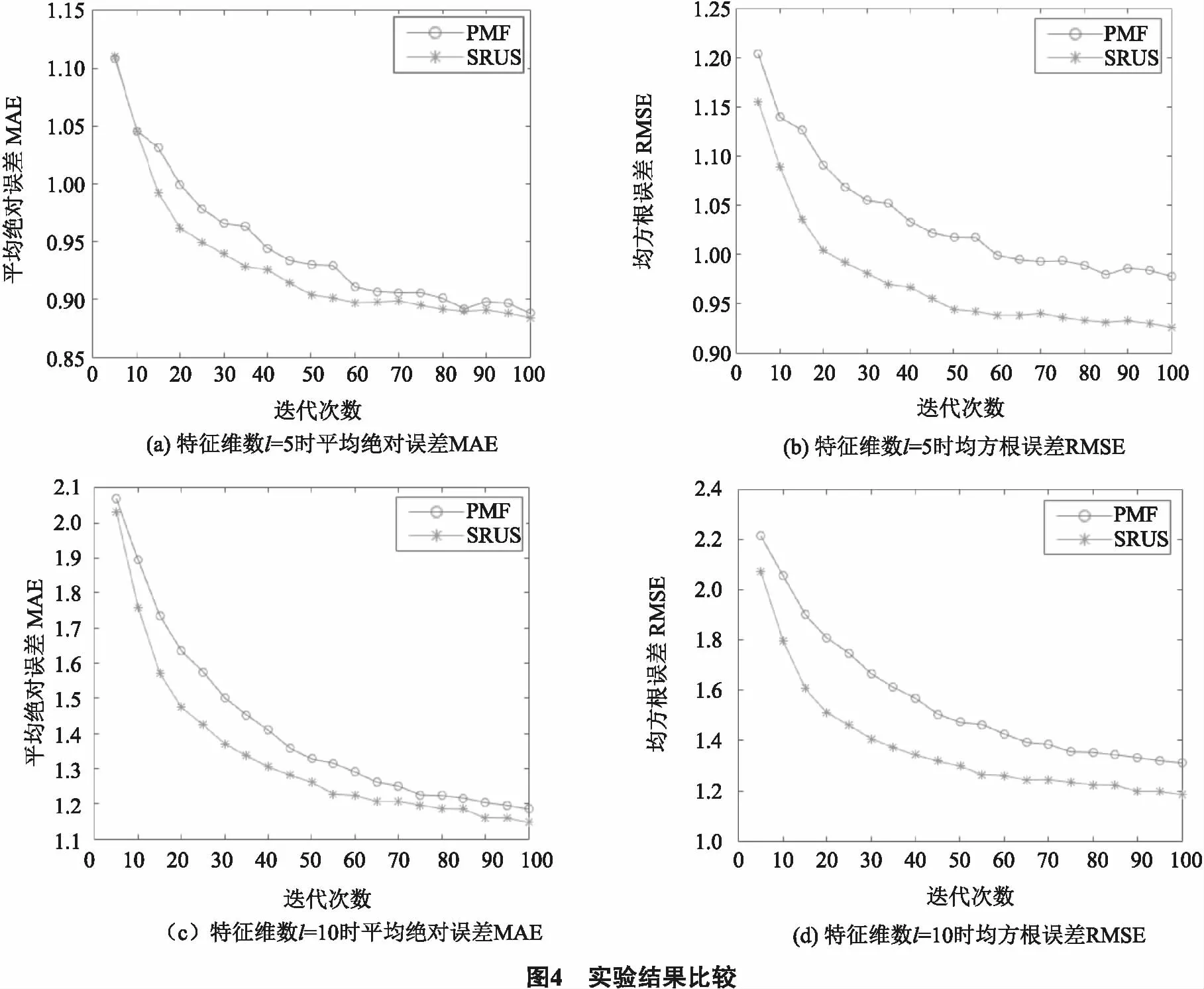
由表5中的数据以及对数据的分析,结合图4的实验结果比较,可以很清晰直观的看出本文提出的SRUS方法较传统PMF方法在指标MAE和RMSE上都得到了降低,有效地提升预测准确率,这也验证本文方法的有效性及可行性.

3 结语

本文提出结合用户相似度的社会化推荐算法,该算法同时考虑用户-项目评分信息和用户相似度信息,并将这2个信息通过PMF模型结合在同一个框架下.在公开的数据集movieslens latest dataset上进行实验,实验结果表明用户相似度对评分预测也起到一定作用,同时也验证在稀疏数据集上所提出的方法提升预测的准确率.将两种因素结合在同一个框架下,通过调整参数的取值,可以适应不同的复杂网络类型,同时对算法复杂度分析,本算法可以扩展到更大的数据集上.因此本文提出的方法在数据稀疏性、用户冷启动和预测准确性等方面具有较好的效果.

虽然该方法对经典CF算法存在的一些问题有所改善,在预测准确性方面也有一定的效果,但使用的相似度计算公式是对称的,并不能准确的表达出两两用户之间喜好的区别,而事实上两两用户的相似度是不一样的,如果对相似度计算采用非对称的方法,无疑会使预测评分更加准确,这也是下一步研究的重点.