带有反对机制的谣言传播模型

任 宁,李金仙

(山西大学 数学科学学院，山西 太原 030006)

自古以来，谣言都是一种重要的消息传播方式[1].不同的书本与文献对谣言有着不同的定义，但它们对谣言的描述都包括“没有事实依据”这一条[2].社会上的每个人都有自己的辨别能力和主观想法，所以他们对待谣言的态度也不一样[3].谣言所引起的人们的恐慌以及各方面的损失是我们不希望看到的[4].因此，谣言传播的过程特征，如何减少谣言传播的危害以及如何引领人们进行谣言相关的预防措施成为了十分重要的研究课题[5].在传统的谣言传播模型中，只考虑了一个人在听到谣言后，或者继续传播，或者不理睬，却没有考虑这个人有可能不赞同这个谣言[6].而在实际谣言传播过程中，有些人不但不传播谣言，还会劝说其他人不要传播，这反映出社会网络本身对谣言传播的一种自发抵抗，这也是本文主要研究的问题[7].同时，为了使动力学方程封闭，利用了概率生成函数的方法[8].通过谣言传播模型的研究，为现实生活中有害谣言的抑制提供了一系列理论依据.

1 SICR谣言传播模型

1.1 定义

根据人群对谣言的态度，将人群分为4大类：未知者，传播者，反对者和沉默者，分别用S,I,C,R来表示它们的密度，且满足S+I+C+R=1[9].设网络中的人群总数设为N，即网络中总节点数为N，网络中的总边数为A.其他参数定义详见表1.

表1 主要参数

续表1

符号定义PIS节点发出的边连接到I节点的概率PSS节点发出的边连接到S节点的概率PCS节点发出的边连接到C节点的概率AX集合X中节点发出的边的数量MX集合X中节点发出的边占网络中所有边的比例AXY集合X中节点发出连接到集合Y中节点的边的数量MXY集合X中节点发出连接到集合Y中节点的边占网络中所有边的比例δXYXY二元组中X节点余度的平均值δXY(Z)δXY条边中连向Z类节点的平均值

1.2 模型的构建

1.2.1SICR谣言传播模型的传播机制

SICR谣言传播模型的传播机制描述为.

1)当一个未知者(S)遇到一个传播者(I)时，可能以概率α变为一个新的传播者；可能以概率β变为一个新的沉默者；可能以概率δ变为一个新的反对者；

2)当一个传播者(I)接触到其他传播者(I)或沉默者(R)时，会以概率γ变为一个新的沉默者；

3)当一个传播者(I)遇到不认同该谣言的反对者(C)时，反对者会尽力说服传播者放弃传播谣言，则该传播者会以概率η变为新的沉默者.

类似于文献[10]的推导，用Sk(t)表示时刻t度为k的节点是未知者的密度，那么我们可以得到

(1)

(2)

(3)

其中θ表示度为1的节点是未知者的概率.

利用度分布pk的概率生成函数，可以得到

S=p0+p1θ+p2θ2+p3θ3=g(θ),

(4)

此式可以用于简化后面的公式.且容易得

(5)

由(1)式，可知

(6)

则

(7)

又由

(8)

得

(9)

且

(10)

为了确定MSI关于时间的导数，可以从3个方面考虑.

1) 在SI二元组中由于传播者对谣言的传播使未知者变成传播者，容易得到MSI减少的比率为(α+β+δ)MSI；

2) 由于未知者的余度邻居的状态的不同导致的MSI的变化.假设任意一个节点其邻居状态之间是相互独立，而且从S出发并且指向其他节点的边数服从多项分布.PS+PI+PC+PR=1，则可以得到未知者节点的余度分布的概率生成函数为

gSI(XS,XI,XC,XR)=g′[θ(PSXS+PIXI+PCXC+PRXR)]/g′(θ).

(11)

由(11)式以及概率生成函数的性质，可以得到以下3个式子

(12)

(13)

(14)

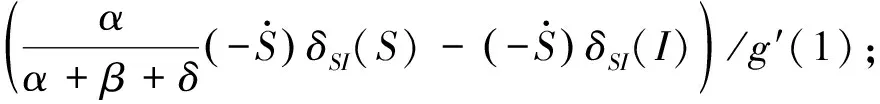
3) 由于SI边中，由于I的恢复，使SI边变为SR边导致的MSI的减少，并利用对逼近的思想，得到MSI减少的比率，用*式表示.

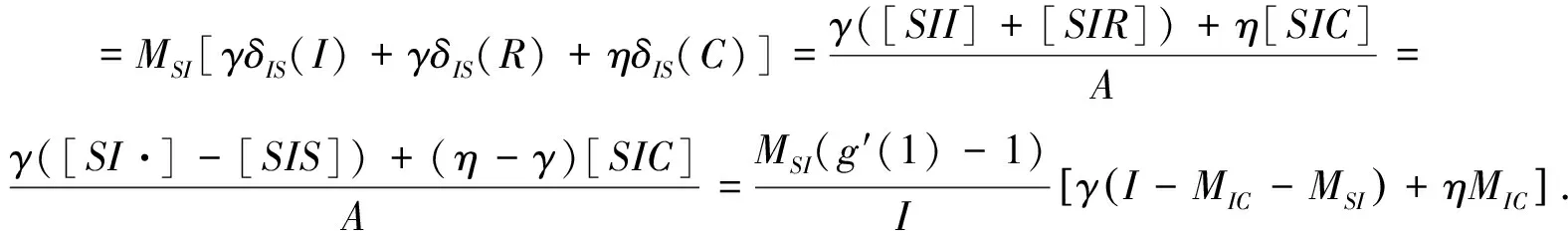
(15)

由此，可以知道

(16)

把公式(8～10)、(16)带入公式(7)可以得到

(17)

类似推理可知

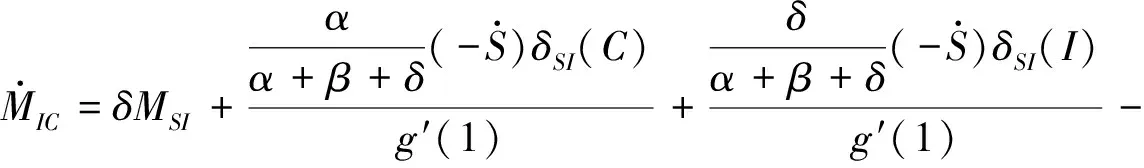
(18)

(19)

(20)

因此 可得到如下封闭系统：

2 理论分析

2.1 初始条件

假设初始时刻网络中的节点被随机选择为传播者的概率为ε，那么可以得到如下的初始条件：

1)MI=ε,MSI≈MI=ε；

2)MS=1-MSI=1-ε,MSS=MS-MSI=1-2ε；

4)MIC=0；

5)θ=1-ε.

2.2 传播阈值

将上面的初始条件应用到公式(17)中，并且注意到ε<<1，我们可以得到：

(21)

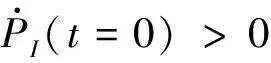
(22)

(23)

3 仿真模拟

下面在泊松网络中进行数值仿真，不失一般性，设这里的网络平均度为4，初始时刻ε=10-3.

从图1中可以看出，传播者的密度随时间的增加而增加直到峰值，之后开始下降.说明谣言传播过程中，传播者的数量一开始会逐渐增多，到达最大值之后开始下降，直到传播者数量趋于0.这时谣言传播终止，网络中不再有谣言出现.

图2显示了SICR谣言模型在不同的参数下，传播者的峰值受参数变化的影响.可以看出传播者的变化总体趋势相同，同时峰值随着α或δ的增大而增大.

图1 传播者密度随时间的变化趋势 图2 传播者的密度随α或δ的增加而变化的情况

4 结语

本文考虑了谣言传播过程中可能出现反对者，所以在经典SIR模型中加入了反对机制，利用了概率生成函数的方法分析了当出现反对者时谣言传播的过程，分析了谣言传播的阈值，并进行了仿真模拟.加入反对者的谣言传播模型体现了现实生活中一部分人对谣言的抵抗，同时概率生成函数是一个十分有效的数学工具，要善于利用概率生成函数进行思考.这个课题还有很多可以做的工作，希望本篇的工作可以为进一步研究提供参考.