基于中智区间函数的岩体边坡稳定性研究
侯钦宽 雍 睿 陈欢欢 沈 飞
(绍兴文理学院 土木工程学院,浙江 绍兴 312000)
性质与边坡工程稳定性评价.
岩体由岩石和结构面组成,岩体发生失稳往往是沿着岩体内部的软弱结构面发生破坏,而不是因为其本身材料的破坏,因此,结构面对岩体稳定性极其重要.岩体结构面的力学性质主要取决于结构面表面的粗糙程度,但是,由于结构面是在漫长的自然历史过程和复杂的地质作用下形成的,其本身具有各向异性、各质异性、非均一性和尺寸效应等特征,会对结构面粗糙度性质的定量描述带来很大困难.因此,深入研究岩体结构面粗糙度尺寸效应和各向异性,并用函数方程定量描述边坡稳定性,将具有重要的理论意义以及实用价值.
数学方法本身是不确定的或方法本身虽确定但可以用来解决自然界和社会科学界中出现的不确定性问题的理论,通称为不确定性理论[1-2].不确定性分析方法主要有可靠性理论[3-5]、模糊数学理论[6-11]、灰色预测系统[12-14]、可拓理论[15-16]、分形几何[17-18]、人工神经网络[19]、蒙特卡洛法[20-22]以及遗传进化算法[23-25]等.中智理论是基于模糊数学发展起来的,近几年逐渐为众人熟知.中智理论在研究客观物体的不确定性方面具有方法简单、适用性强等优势.岩体结构面力学参数的不确定性主要是由其本身的复杂特性所决定的,而其同时具有的各向异性、各质异性、非均一性和尺寸效应[26],共同导致了其力学参数存在模糊性.中智理论可将力学参数的模糊性包含在一定的集合范围内,对岩体结构面的力学效应进行综合识别和判断,从而得到更为符合客观实际的解答.
中智理论包含中智集、中智数、中智区间函数等概念.Smarandache[27]首先提出中智集的概念.为了将简化的中智集应用到实际的不确定性问题中,Wang[28]和Ye[29]定义了单值中智集及其集结算子.Ye[30]在此基础上定义了区间值中智集的距离和相似度.王坚强[31]认为,不确定性无法给出一个确定的值或区间,因此定义了多值中智集.中智数的概念也是由Smarandache[32]首次提出,它通过定义一个中智数Z=a+bI来描述确定的或不确定的信息.Ye和Chen[33-34]等首次将中智数与岩石节理粗糙度系数JRC相结合,用中智数来描述JRC尺寸效应和各向异性的不确定性.中智区间函数同样是由Smarandache[32]首先提出,它是一种通过定量区间描述事物不确定性的方法.Yong[35]将中智区间函数应用于表达结构面粗糙度系数和抗剪强度的尺寸效应不确定性.然而,上述大部分研究主要从JRC以及相关参数来描述尺寸效应和判断边坡稳定性,未能准确表达结构面粗糙度系数的不确定性分布规律,未能将尺寸效应的影响应用于边坡分析及确定稳定系数中.
为了解决当前边坡稳定性评价中因结构面复杂特性而引起的力学参数的不确定性问题,本文基于中智区间函数能更好地表达事物的不确定性的特点,将边坡结构面粗糙度、抗剪强度和边坡稳定系数控制在一个区间之内,使边坡稳定性评价更为符合客观实际.
1 中智区间函数表达
中智区间函数可用于解决各领域所存在的不确定性问题.其原理是定义一个区间映射函数f:R→F(R),f(x)=[ax,ax+b],x∈R,R是实数,a和b表示区间函数参数,它通过一个区间映射函数,将所描述的不确定的事物包含于一个区间之内,通过区间来描述事物的不确定性.其具体计算方法如下:
假定中智区间函数f:R→F(R),f(x)=[2x,2x+3],x∈R,R为实数,F(R)是R所有子集中的一个.因此,从图1可以看出,当x=-5时,有
f(-5)=[2×(-5), 2×(-5)+3]
=[-10,-7],
同理,当x=5时f(5)=[10,13].图1中的灰色区域即不确定范围,它的区间函数是在f1(x)=2x到f2(x)=2x+3之间.
综上所述,我们定义中智区间函数f:R→F(R)为f(x)=[f1(x),f2(x)].例如,当x=1时,f(1)=[f1(1),f2(1)],中智区间函数值即为在x=1时的竖直线段,即[f1(1),f2(1)].我们也可以定义中智函数开区间f(x)=(f1(x),f2(x))或者半开区间f(x)=[f1(x),f2(x))=(f1(x),f2(x)].

图1 中智区间函数计算示意图
2 基于中智区间函数的边坡稳定性表达
2.1 结构面粗糙度系数尺寸效应的中智区间函数表达
结构面粗糙度系数尺寸效应指的是粗糙度在不同的结构面尺寸下存在不同的值.在实际工程中,由于结构面的复杂特性,结构面粗糙度存在不确定性,以往计算JRC仅仅是选用平均值,忽略了数据的离散性,因此,我们引入中智区间函数,用区间表达来描述结构面粗糙度的不确定性.
选择合适的区间范围是中智区间函数的关键.引入概率学中的稳健性概念,稳健性指的是数据在发生日常波动的条件下,所讨论的问题仍在其平均值处的变异程度(如标准差),且数据在一个合理范围之内可以承受极端数据所带来的误差,不至于整体数据失效.
从工程角度来说,由于测量手段、测量对象、测量人员的原因,所测结果往往存在极端误差,倘若使用最大最小值作为区间范围势必会顾此失彼,因此我们将选用稳健性区域作为中智函数的区间范围,在保证区间合理性的同时降低数据对极端误差所带来的敏感性.以一个系列尺度下的JRC值为例,见图2,10 cm时JRC平均值为13.46,标准差为4.21,变异程度区间为[13.46-4.21,13.46+4.21].经过统计分析发现,在该系列尺度下,有70%左右的样本分布在此区域内,我们将这个区域称为稳健区域.
综上,为了描述系列尺度下JRC的不确定性,以JRCmean+σ作为中智区间函数的上界,以JRCmean-σ为中智区间函数的下界,其中σ表示该组JRC数据的标准差.
JRC存在尺寸效应,其值随取样长度的增大而降低.Barton[36]在对200多条人工拉断节理进行详细研究的基础上,得出JRC尺寸效应公式:

图2 系列尺度下JRC尺寸效应分布示意图
JRCn=JRC0×(Ln/L0)-0.02JRC0,
(1)
式中:JRC0为标准结构面试验长度(10 cm)下的粗糙度系数;Ln为所测结构面的长度;L0为实验室标准试样长度(L0=10 cm).
杜时贵[26]对1157个不同取样长度的JRC值实测资料进行统计分析,发现JRC的尺寸效应规律具有各质异性和各向异性.一般而言,JRC较小的轮廓曲线,其JRC尺寸效应比JRC较大的轮廓曲线更显著.这篇文章指出,式(1)是平均公式,JRC尺寸效应规律应表示为:
JRCn=JRC0×(Ln/L0)-aJRC0,
(2)
式中:a称为JRC尺寸效应修正系数.
从上述两式可以看出,考虑到结构面的复杂特性,公式的指数并不确定.为了简化计算,本文将指数-a×JRC0以参数b代替,式(2)表述为:
JRCn=JRC0×(Ln/L0)-b.
(3)
如图3所示,对10~100 cm系列尺寸结构面轮廓曲线进行拟合,可以得出JRC中智区间函数的下界为:
JRC-(L)=9.25×(L/10)-0.39.
JRC中智区间函数的上界为:
JRC+(L)=17.67×(L/10)-0.44.
结合中智区间函数的下界和上界,可以得出JRC在系列尺寸下的中智区间函数表达式:
JRC(L)=[JRC-(L),JRC+(L)]=
[9.25×(L/10)-0.39,17.67×(L/10)-0.44].

图3 JRC尺寸效应中智区间函数
2.2 结构面抗剪强度的中智区间函数表达
了解与掌握岩体的变形与破坏规律是岩体结构面粗糙度研究的主要目的之一.抗剪强度作为岩体结构面的重要力学参数之一,对岩体稳定性评价具有非常重要的作用,建立粗糙度与抗剪强度之间的关系一直是岩体力学的热门研究课题.
JRC-JCS模型是Barton[36-37]于1977年在大量原位岩体结构面直剪试验的基础上提出的,其表达式如下:
(4)
式中:JCSn为结构面壁岩强度;φb为基本摩擦角;σn为有效法向应力.
基于JRC-JCS模型,将中智区间函数的结构面粗糙度系数表达式代入其中,可推导得出抗剪强度的中智区间函数的表达式:
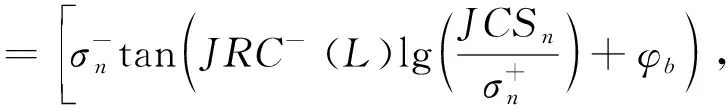

(5)
其中,根据试样的JCS0值,利用壁岩强度尺寸效应公式确定大尺度试样结构面的壁岩强度JCSn.尺寸效应修正公式为:
(6)
式中:JCS0为标准结构面试验长度(10 cm)下的结构面壁岩强度.
2.3 边坡稳定系数的中智区间函数表达
本文以单平面滑动模型为例进行分析.已知坡角i,滑体高H,潜在滑动面角度β,计算模型如图4所示,则潜在滑体ABC的相关参数可以依据以下公式计算:
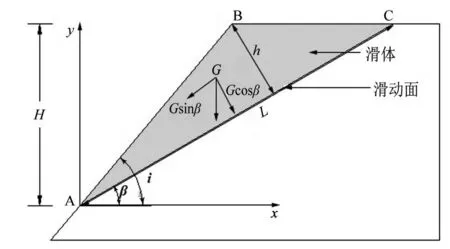
图4 平面滑动稳定性计算模型
(7)
式中:ρ为滑体平均密度;g为重力加速度(9.8 m/s2);L为潜在滑动面AC的长度;G为滑体重力.分别计算滑体ABC的下滑力Fr和抗滑力Fs:
(8)
式中:φ为结构面的内摩擦角;c为结构面的黏聚力.进而得到边坡稳定系数:
即边坡稳定系数计算公式:
(9)
结合中智区间函数,可得到边坡稳定系数的中智区间函数表达式:
(10)
由式(9)和式(10)可知,边坡稳定系数中智区间函数计算公式的主要影响参数包括结构面的黏聚力c和结构面的内摩擦角φ.本文抗剪强度计算模型为Barton的JRC-JCS模型,考虑到参数不一致,我们将基于JRC-JCS模型进行等效参数转化,得到等效的摩尔-库仑参数ci和φi.等效参数转化示意图如图5所示[38],转化过程如下.
等效内摩擦角φi的计算方法如下:
(11)
其中
(12)
等效黏聚力ci则用下面公式表示:
ci=τ-σntan(φi).
(13)
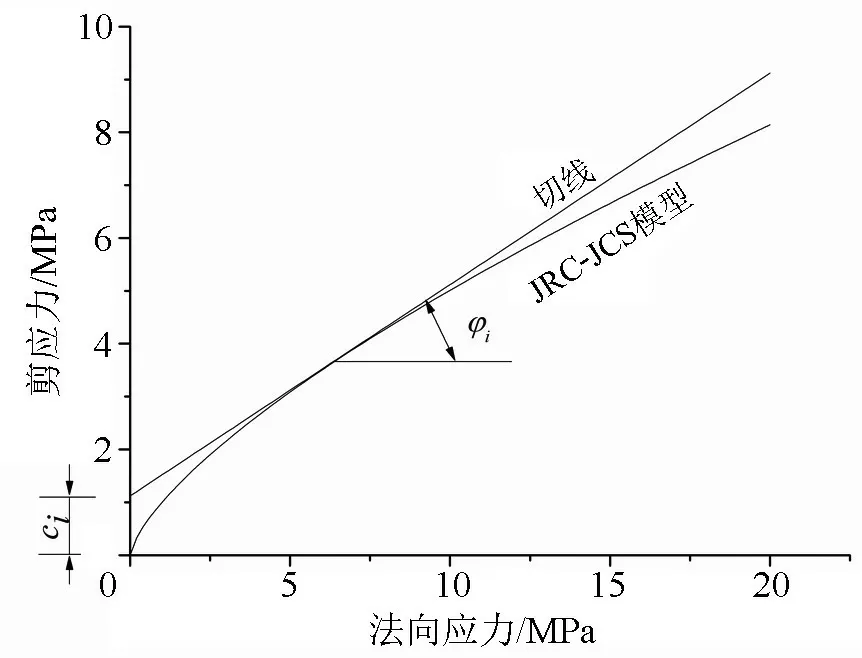
图5 等效参数转化示意图
3 实例分析
3.1 工程概况
野外现场选定浙江省嘉兴市海宁黄湾镇岳庙山矿山,测量其边坡基本参数.边坡近东西走向,倾向北,长103 m,宽度103 m,坡高57 m,边坡坡角i为58°,坡向10°,滑体高度28.5 m,滑动面长度L为40.30 m,滑动面倾角β为45°,滑体天然容重为29 kN/m3,计算模型如图6所示.
3.2 结构面粗糙度系数尺寸效应的中智区间函数表达
在该大尺寸天然结构面的表面沿潜在滑移方向等间距布置测线,采用简易纵剖面仪分别绘制10 cm,20 cm,…,100 cm的结构面表面轮廓曲线,进而选用简明直边法计算所有轮廓曲线的JRC值,对该JRC值进行数理统计分析,得出系列尺寸下JRC的均值JRCmean和标准差σ.
计算得到该系列尺度下10 cm时JRC平均值为6.12,标准差为1.25.我们以JRCmean+σ作为中智区间函数的上界,以JRCmean-σ作为中智区间函数的下界,则变异程度区间为[6.12-1.25,6.12+1.25]=[4.87,7.37].将工程实际数据代入其中,根据公式(3),通过折线统计图对JRC进行拟合,建立尺寸效应评价指标,得到参数b,因此可以得出JRC尺寸效应中智区间函数,函数图像如图7所示.
由此可以得出JRC中智区间函数的下界为:
JRC-(L)=4.87×(L/10)-0.075,
JRC中智区间函数的上界为:
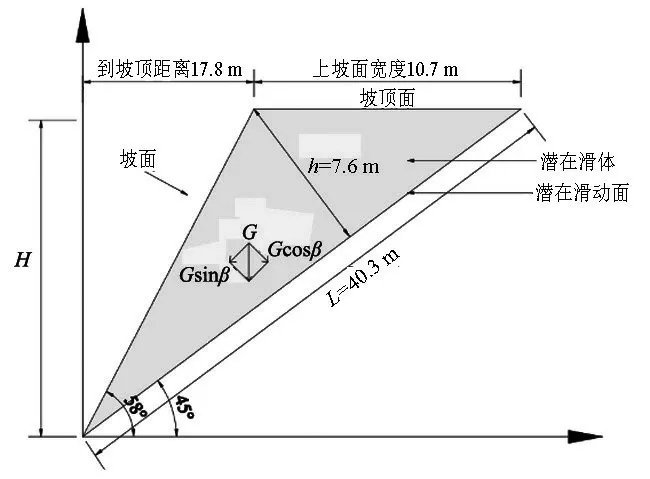
图6 岳庙山矿山边坡稳定性计算模型

图7 JRC尺寸效应中智区间函数
JRC+(L)=7.37×(L/10)-0.081.
结合中智区间函数的下界和上界,可以得出JRC在系列尺寸下的中智区间函数表达式:
JRC(L)=[JRC-(L),JRC+(L)]=
[4.87×(L/10)-0.075,7.37×(L/10)-0.081].
则当L=40.3 m时,计算得到结构面粗糙度下限为JRC-(L)=4.87×(4030/10)-0.075=3.11,结构面粗糙度上限为JRC+(L)=7.37×(4030/10)-0.081=4.53.
3.3 结构面抗剪强度的中智区间函数表达

τ(4030)=[τ-(4030),τ+(4030)]

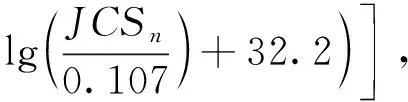
此时抗剪强度的中智区间函数图像见图8,继而可知,当L=40.3 m时,JCSn为42.34 MPa,此时的抗剪强度区间为
τ(4030)=[0.091,0.104] MPa.
3.4 边坡稳定系数的中智区间函数表达
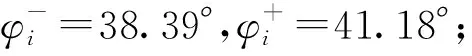

图8 抗剪强度中智区间函数图像
最后,将得到的抗剪强度参数代入边坡稳定系数计算公式(9)中,得:
=0.868,
=1.000.
由上述计算可得,结构面长度为40.3 m条件下,该岩质边坡的稳定系数下限为0.868,上限为1.000,由式(10)可得此时稳定系数的中智区间范围为
[FS-,FS+]=[0.868,1.000].
边坡稳定性计算含有若干不确定性,计算精度很难达到100%[39],导致计算结果具有一定的模糊性.用中智区间的形式可以更好地表达这种模糊性.本文采用矿山边坡国家标准规范[40]来评价边坡稳定性,根据规范,该边坡的设计安全系数为1.15~1.10,实际计算稳定系数中智区间均小于此范围,边坡不稳定,可能沿潜在滑移面发生单平面型滑移的情况,进而产生破坏.
4 结论
岩体结构面具有各向异性、各质异性、非均一性和尺寸效应等复杂特性,这都严重增加了对结构面粗糙度性质定量描述的难度.本文结合中智区间函数,提出了结构面粗糙度系数尺寸效应的表达方法,并定量表达了结构面粗糙度系数的不确定性.
结构面抗剪强度参数具有离散性和模糊性,基于中智区间函数将结构面抗剪强度参数控制在稳健区间内,考虑了参数不确定性对边坡稳定性评价的影响,使其更为符合客观实际.本文提出的方法还可应用于评价不同类型工程的稳定性.

