轨道车辆车内压力与车体气密性、侧墙刚度、车外压力变化的关系研究

王前选，胡哲龙，梁习锋

（1.五邑大学 轨道交通学院，广东 江门 529020；2.中南大学 交通运输工程学院，湖南 长沙 410075；3.今创集团有限公司，江苏 常州 213011）

安全、快捷、舒适是现代先进轨道交通追求的三大目标[1]. 我国地铁列车运行速度已达到120 km/h，城际列车运行速度已达160 km/h，京沪、京广、沪昆等客运专线列车运行速度已达300 km/h.随着运行速度不断提高，当列车高速通过隧道时，车头前部的空气被压缩形成压缩波向隧道出口传播，当传递到隧道出口时，由于隧道口空气边界气压的反射作用而变为膨胀波，再向隧道入口传播.当列车尾部进入隧道时，在隧道入口处产生膨胀波，该膨胀波在传播到隧道出口时变成压缩波，再由隧道反方向向隧道入口传播. 当压缩波和膨胀波相遇时，产生叠加效应，导致隧道内空气压力发生剧烈变化[2]. 当列车高速在隧道内交会时，车外压力将发生更加剧烈的变化，该压力波向车内传递造成车内压力波动，列车速度越高，车内压力绝对值和波动速度越大，给乘车舒适性和安全性带来严重影响，会引起乘客头晕、耳鸣、恶心、呕吐等现象[3-5]，甚至造成耳膜破裂. 高速列车车内压力变化对乘车舒适性造成不良影响引起国内外学者广泛关注[6-9]，国内外学者采用实验和数值计算等方法，对车外压力向车内传递的规律、车内压力变化、车内压力变化控制指标等方面进行了研究[10-12]，但对列车过隧道或在隧道内交会时车内压力变化的影响因素和影响机理研究较少.

本文首先探明车体气密性和车体侧墙刚度是影响高速列车车内压力变化的主要因素，在此基础上，分别设计大刚度非密闭车体模型、不同刚度密闭车体模型、不同刚度非密闭车体模型，通过实验得出：车体模型气密性与车内外压力变化关系式、车体模型侧墙刚度与车内外压力变化关系式，以及车体模型气密性、车体侧墙刚度与车内外压力变化关系式，以期为科学合理制定轨道车辆车体气密性指标、控制车内压力变化具体措施提供理论支撑.

1 影响车内压力变化的因素

为研究这一问题，本文进行了“中华之星号”和“长白山号”高速列车在遂渝铁路（遂宁市—重庆市）列车交会和列车通过隧道的空气动力学实车实验. 如图1所示，在这两种高速列车车厢内布置三维动态空气压力测点，6个动态压力传感器组合成1个三维压力传感器（如图2-a），对应车体纵向、垂向、横向各有2个传感器，共有6个测点，分别指向列车前后端、车顶与地板、车窗玻璃与室内（如图2-b）.

图1 中华之星号和长白山号高速列车车内三维动态压力传感器布置

图2 三维压力传感器及布置示意图

中华之星号高速列车交会现场空气动力学实验车内压力变化见表1，其中正对车窗测点所处位置在两列车交会侧，朝前表示列车前进方向. 从表1可以看出，中华之星高速列车车内压力变化与车内动态压力传感器的放置方位有关，在置于车内的6个动态压力传感器中，正对交会侧车窗玻璃方向的传感器感受的压力最大，即正对车窗的测点压力变化最大，其幅值是其他方向的2～4倍.

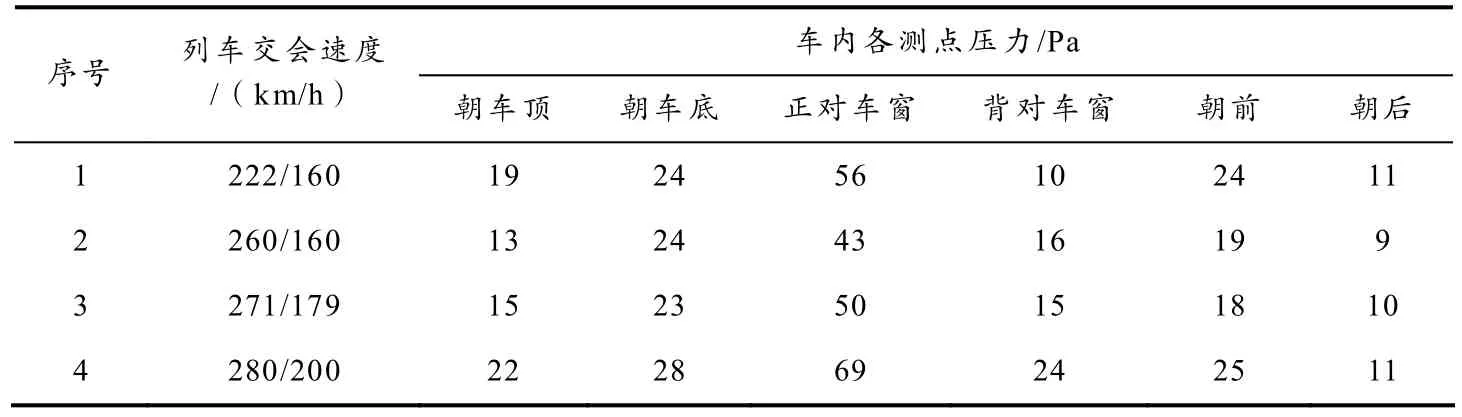
表1 中华之星号高速列车交会现场车内的压力变化

长白山号列车高速通过隧道现场空气动力学实验车内压力变化见表2，其中正对车窗测点所处位置在车体靠近隧道壁一侧，朝前表示列车前进方向. 从表2可以看出，长白山号高速列车以同一速度通过隧道时，车内压力变化与车内动态压力传感器的放置方位亦有关，正对车窗测点的压力明显大于其他方向的，背向列车前进方向即朝后测点的压力明显小于其他方向的，而朝车顶、朝车底、背对车窗和朝前测点的压力相差不大.

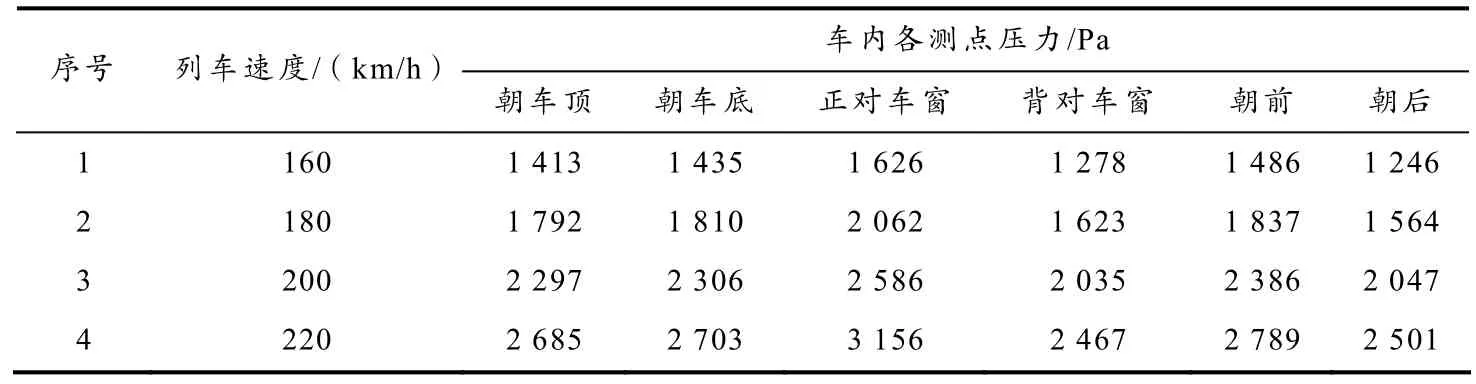
表2 长白山号高速列车通过隧道时车内的压力变化

综合表1和表2可以看出，正对车窗测点的压力远大于其他测点的压力，这是由列车交会或列车通过隧道时车体侧墙发生微小变形导致的. 因此，当列车高速交会和高速通过隧道时，车内压力变化不仅与车体气密性有关，还与车内外压力差引起的车体侧墙微小变形有关，车体侧墙变形与车体侧墙刚度紧密相关，即影响车内压力变化的因素是车体气密性和车体侧墙刚度.

2 车内压力与车体气密性、车外压力变化的关系

为研究车内压力与车体气密性、车外压力变化关系，设计制作气密性不同的车体模型作为研究对象，不同泄压时间通过在密闭车体模型上开不同孔径的细微孔来实现. 制作 5种不同孔径的大刚度车体模型，车体模型尺寸为250 mm× 6 0 mm× 7 0 mm ，在车体模型表面开一个圆孔作为泄压孔. 将被试车体模型固定在交变压力实验台密闭室内，密闭室一端为密封门，另一端是可运动的活塞，活塞与交变压力模拟实验台密闭式内壁采用柔性密封连接. 活塞一端与密闭室相连，另一端连接在曲柄连杆机构上. 通过调速电动机带动曲柄连杆机构运动，曲柄连杆机构则带动活塞往复运动，使密闭室的容积反复发生变化，密闭室内将产生周期性的压力变化. 调节曲柄连杆机构转速可控制密闭室压力变化的频率，调节偏心轮偏心距可控制密闭室压力变化的幅度，这样就可以模拟车体外部空气压力变化情况. 将车体模型先后置于交变压力模拟实验台密闭室中进行实验. 分析相同压力变化周期下的不同气密性车体车内压力变化率数据可以得出：车体模型气密性与车内压力变化率基本呈幂函数关系：

其中，f为车内空气压力变化率；t为车体泄压时间；a,b为常数，a值由车外空气压力变化幅值决定，b≈-0.5.

分析相同泄压时间、不同压力变化周期工况下车内压力变化率与车外压力峰值数据可以得出：车内压力变化率与车外压力变化幅值基本呈线性关系：

其中，f为车内空气压力变化率；x为车外压力变化幅值；c为系数，其值大小与车体气密性有关.

由式（1）和式（2）可以得出，大刚度车体车内空气压力变化率和车体气密性、车外空气压力变化幅值存在如下关系：

其中，f为车内空气压力变化率；x为车外压力变化幅值；t为车体泄压时间；m,b为常数，m的值与车体气密性和车外压力变化相关.

3 车内压力与车体侧墙刚度、车外压力变化的关系

为研究车内压力与车体侧墙刚度、车外压力变化关系，设计制作刚度不同且密闭的车体模型作为研究对象. 采用不同的材质和板厚制作了 5种不同刚度的全密闭车体模型，其空心内腔尺寸为250 mm× 7 2 mm× 6 0 mm ，车体模型端墙、顶部和底部的厚度均为5 mm，材料都采用Q235；车体模型不同之处在于不同模型的两面侧墙选用不同厚度或材料的金属板来焊接（或胶接），模型车体侧墙刚度不同主要是其自振频率不同所致[13-16]. 对5种车体模型进行有限元模态分析，车体模型采用壳单元 shell63进行离散，Q235弹性模量为206 GPa、密度为 7 .8 g/cm3；铸锌铝合金弹性模量为71 GPa、密度为 6 .75 g/cm3；泊松比均取0.3.

通过计算得到5种车体模型的自振频率. 将5种不同刚度的车体模型分别固定在交变压力实验台密闭室内进行实验，通过交变压力实验台模拟车体外部空气压力变化. 分析车体模型自振频率相同条件下车体模型车外压力峰值与车内压力变化率数据，得出：相同侧墙刚度的车体模型，其车内压力变化率随车外压力变化峰值的增大而增大，呈二次曲线关系：

其中，f为车内空气压力变化率；x为车外压力变化幅值；g,h为系数；m为常数.

分析车体模型车外压力变化幅值相近的条件下不同自振频率车体模型车内压力变化率数据，可以得出：当车体模型车外压力相近时，车体模型车内压力变化率随车体模型自振频率的增大而减小；当车体模型车外压力变化幅值一定时，车内压力变化率和车体模型自振频率呈幂函数关系变化：

其中，f为车内空气压力变化率；y为车体模型自振频率；d,n为系数，本文中d与车体模型车外压力变化幅值有关，n≈2.74.

由式（4）和式（5）可以得出：不同刚度密闭车体模型，其车内压力变化率与车体模型侧墙刚度、车外空气压力变化幅值存在如下关系：

4 车内压力与车体气密性、侧墙刚度、车外压力变化的关系

导致车内压力发生波动的主要因素是车体气密性和车体侧墙刚度，因此，在设计高速列车时，一方面需要提高车体气密性，另一方面需要加大车体侧墙刚度. 当高速列车交会或通过隧道时，高速列车车内压力变化由两部分组成：一部分是由于车体的气密性不良，车外压力通过车体缝隙传递到车内，造成车内压力产生变化；另一部分是由于车体侧墙发生变形，导致车内空间容积产生变化，造成车内压力变化. 即，车内压力变化率与车体气密性、车体侧墙刚度、车外压力变化幅值存在如下关系：

其中，f(x,y,t)是同时考虑车体气密性、车体侧墙刚度时的车内压力变化率；f(x,y)是不同刚度密闭车体车内压力变化率；f(x,t)是大刚度非密闭车体车内压力变化率；α为车体侧墙刚度对车内压力变化的影响系数；β为车体气密性对车内压力变化的影响系数.

前文中f(x,y)和f(x,t)的表达式已经得出，但需要确定α和β的值. 如果车体气密性不好，车外压力波动通过车体缝隙传入车内，而车体侧墙刚度对这一传递过程基本不产生影响，所以系数β≈1. 当车体内外存在压力差时，车体侧墙发生微小变形，而如果车体气密性不好，车体侧墙内外两侧所受到的压力差比车体全密闭情况下侧墙内外两侧所受到的压力差会小一些，车体侧墙的变形量也会减小，从而削弱车体侧墙刚度对车内压力波动的影响，即车体气密性对由于车体侧墙变形引起的车内压力变化率大小有影响.

为研究车体气密性随车体侧墙变形引起的车内压力变化率的影响，制作三组共 15种不同气密性、不同刚度的车体模型，每组车体模型侧墙刚度不同、车体气密性相同. 车体模型尺寸形状与前文不同刚度密闭车体模型相同，具体设计方案见表3.

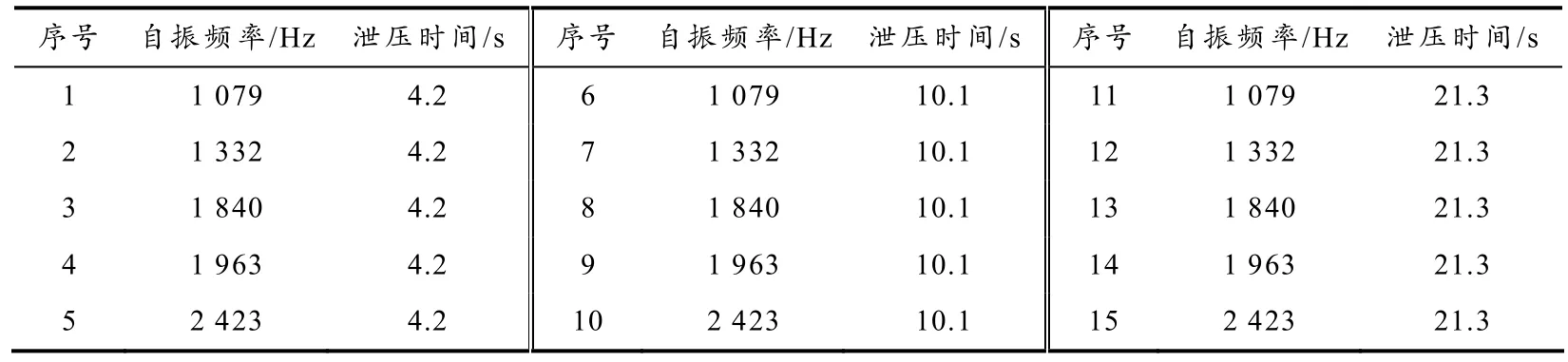
表3 不同气密性、不同刚度的车体模型设计方案

将上述15种车体模型及其对应的5种大刚度非密闭车体模型分别固定在交变压力实验台密闭室内，通过交变压力实验台模拟车体外部空气压力变化，当车体模型车外压力变化周期为0.19 s、车外压力变化幅值为5 000 Pa左右时，不同刚度密闭车体模型、大刚度非密闭车体模型和非大刚度非密闭车体模型车内压力变化数据见表4.

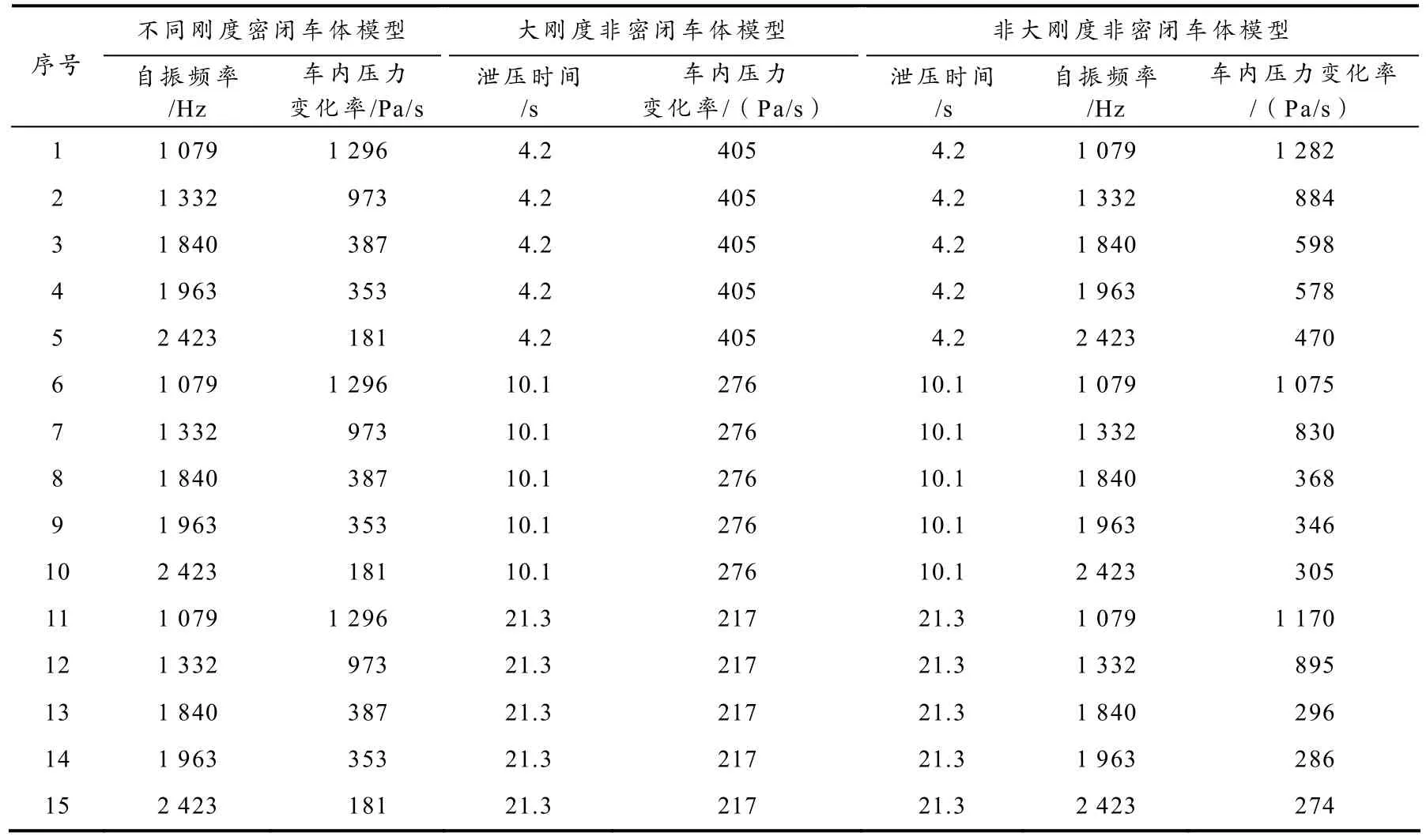
表4 不同刚度密闭、大刚度非密闭和非大刚度非密闭车体模型车内压力变化数据

将不同刚度密闭车体模型、大刚度非密闭车体模型和非大刚度非密闭车体模型车内压力变化率数据取出来分析，获得的车内压力变化率数据比较如图3所示.

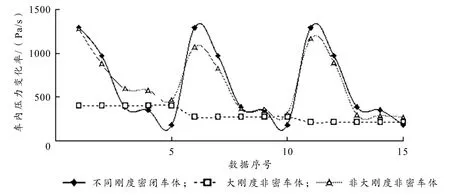
图3 不同刚度密闭、大刚度非密闭和非大刚度非密闭车体模型车内压力变化率

由图3可以得出，当不同刚度密闭车体模型车内压力变化率（仅考虑车体侧墙刚度对车内压力变化的影响）大于大刚度非密车体模型车内压力变化率（仅考虑车体气密性对车内压力变化的影响）时，非大刚度非密车体模型车内压力变化率（同时考虑车体侧墙刚度和车体气密性对车内压力变化的影响）介于不同刚度密闭车体模型和大刚度非密车体模型车内压力变化率之间. 当不同刚度密闭车体模型车内压力变化率小于大刚度非密车体模型车内压力变化率时，非大刚度非密车体模型车内压力变化率分别大于不同刚度密闭车体模型、大刚度非密车体模型车内压力变化率. 基于此，拟定系数α的表达式如下：

将式（7）代入式（6）计算得出车内压力变化率的理论值见表5.

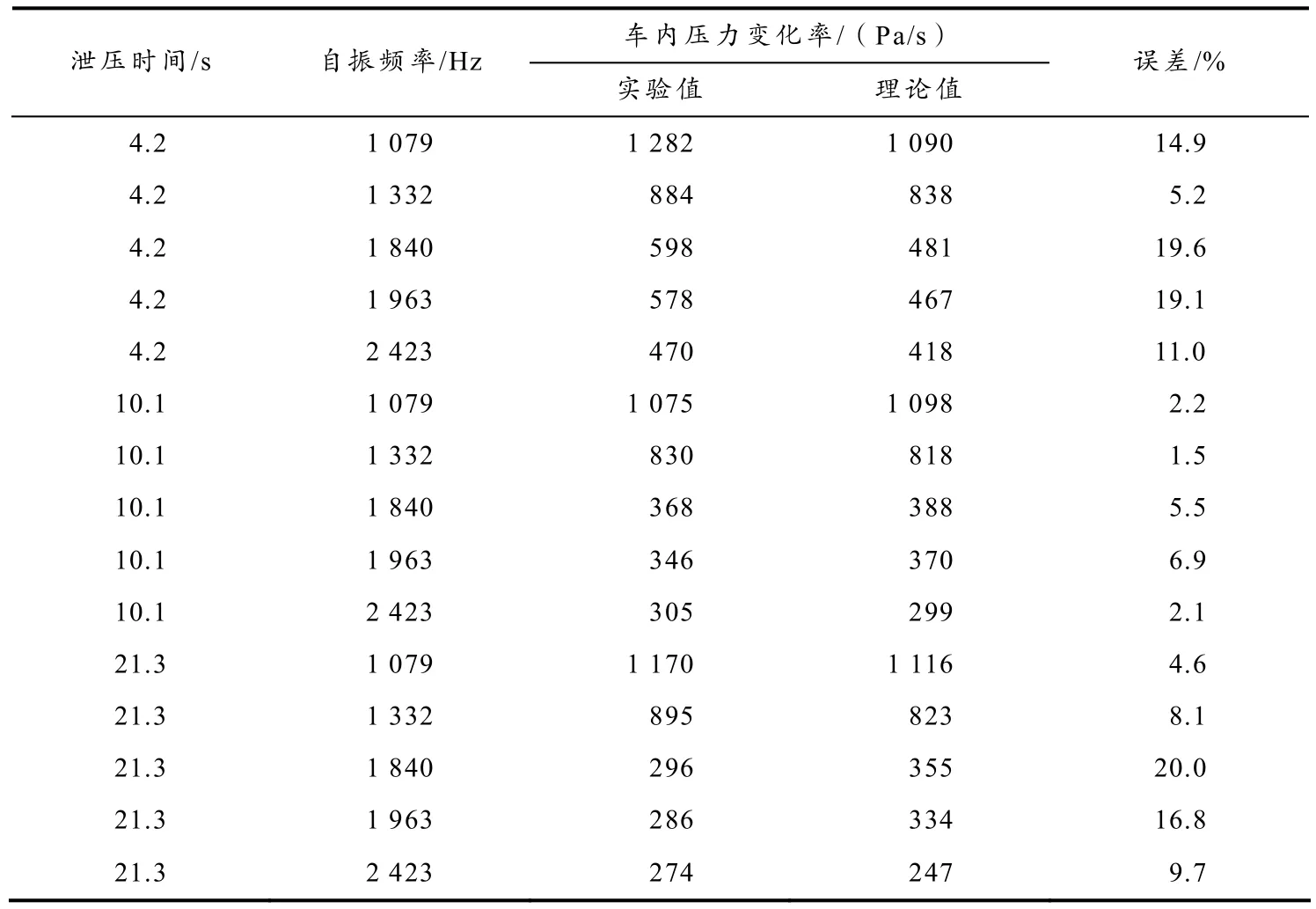
表5 非大刚度非密车体模型车内压力变化率实验值与理论值比较

由表5可以看出，车内压力变化率理论值与实验值误差有三分之一处于10%～20%之间、三分之二处于 10%以内，平均误差在 10%以内，说明式（7）所拟定的系数α值是可信的；而实验值与理论值存在较大误差，是由于交变压力实验台在加载车外模拟压力时，不同车体模型车外压力幅值不完全一致造成的.

5 结论

列车高速交会和通过隧道时，车体气密性、车体侧墙刚度、车外压力变化是影响车内压力波动的主要因素，不同气密性、不同刚度的车体模型其车内压力与车体气密性、侧墙刚度、车外压力变化满足关系式：f(x,y,t) =αf(x,y) +βf(x,t)，式中f(x,y,t)是同时考虑车体气密性、车体侧墙刚时的车内压力变化率；f(x,y)是不同刚度密闭车体车内压力变化率；f(x,t)是大刚度非密闭车体车内压力变化率；α为车体侧墙刚度对车内压力变化的影响系数，且α≈f(x,y)2(f(x,y) + 1 .5f(x,t))2；β为车体气密性对车内压力变化的影响系数，且β≈1. 但结论还需采用实际车体进行试验验证，进一步准确确定α、β值，为新造高速列车车体气密性、侧墙刚度设计提供理论依据.