MUSIC算法的GPU高效实现
朱新峰,陆小霞,黎仁刚,王国海,王彦凌
(1.扬州大学,江苏 扬州 225001;2.中国船舶重工集团公司第七二三研究所,江苏 扬州 225101;3.中电科航空电子有限公司,四川 成都 611731;4.浙江理工大学,浙江 杭州 310018)
0 引 言
空间谱搜索[1]是阵列信号处理中的一个重要研究方向,在雷达、通信、声呐等众多领域有着极为广阔的应用前景。目前对于空间谱搜索主要用信号子空间类方法[2]来处理。信号子空间类方法主要由2步组成:一是对接收数据协方差矩阵进行正交分解来估计信号(或噪声)子空间;二是进行谱峰搜索来提取波达方向估值。无论是正交分解还是谱值计算都面临着巨大的运算量。在信息技术的不断更新中,传统测向技术[3]已经无法满足当下的需求,因此以MUSIC算法为代表的超分辨测向算法应运而生[4]。然而MUSIC算法中接收矩阵的子空间分解部分计算量庞大,影响了计算效率。为了高效实现MUSIC算法,因此考虑将MUSIC算法放在GPU下去实现,GPU可以提供数十倍乃至于上百倍于CPU的性能,能够明显提升运行的速度。
1 MUSIC原理和运算流程
1.1 MUSIC原理
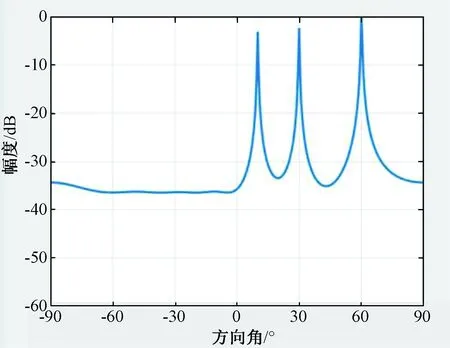
在经典窄带MUSIC算法中,通常要求入射信号源数目小于阵元数,即P 设快拍数为N,根据式(1)所示接收数据模型,可求得阵列接收数据的协方差矩阵Rxx为: Rxx= E[x(t)xH(t)]= AE[s(t)sH(t)]AH+E[n(t)nH(t)]= ARssAH+σ2I (1) 式中:E[*]表示求算数平均;Rss表示原始信号的协方差矩阵,当信号间相互独立时,Rss为P维对角矩阵,对角线上值为对应位置信号的平均功率;σ2为噪声功率;I为M维单位矩阵。 因为相互独立的假设前提,不同阵元噪声间、信号与噪声间的协方差值接近0,所以接收数据的协方差矩阵可近似为信号矩阵的主对角线上加上噪声功率。对Rxx进行奇异值分解,得到特征向量矩阵U、V和对应特征值组成的对角矩阵Σ: Rxx=UΣV (2) 式中:Σ对角线呈递减排列时,可根据值大小将特征向量矩阵分为信号子空间Us与噪声子空间Un。 (3) U=[UsUn] (4) 奇异值分解所得的特征向量两两正交,所得信号子空间与噪声子空间必然正交,且信号子空间与入射信号阵列流形张成的空间一致,所以阵列流形中任意导向矢量与噪声子空间正交。 aiUn=0,i=1,2,…,P (5) 但在实际情况中,由于噪声的存在,以及入射信号复包络近似不变的假设,导致估计结果存在一定偏差,导向矢量与噪声子空间不可能完全正交。 因此,通过扫描不同入射角构造各来波方向上的阵列流形,求取式(3)模值平方,取得极小值的点即为来波方向,如式(6): (6) 式中:argmin{*}表示求*最小值时扫描变量的值。 为了更加直观地表示来波方向,且使接近的2个峰值更易于分辨,绘制空间谱图时通常取倒数,如式(7): (7) 式中:Pmusic表示空间谱。 根据MUSIC算法的基本原理,绘出MUSIC算法的一般流程,如图1所示。 图1 MUSIC算法流程图 以五元非均匀阵列为目标阵形,入射方向分别为10°,30°,60°,信噪比为10 dB,高斯白噪声为500的线性调频信号作为入射信号,MUSIC算法计算出的空间谱如图2所示。 图2 5元阵空间谱 图2中,3个最大谱峰处的方向角坐标值即为来波方向,算法能够准确估算出3个入射信号的方向,具有优越的多信号同时测向能力。 在时间上,算法中阵元数为9,使用信噪比是60,中心频率是18e9,带宽是20e6,采样频率是40e6,根据上面数据计算出采样时间、快拍持续时间、频率变化率,并在Matlab平台下进行仿真,如图3所示。 图3 九元阵方向角空间谱 使用的总时间为2.148 926 s,并且单独测试了计算占用时间、接收矩阵、协方差计算、奇异值分解(SVD),谱峰搜索分别稳定在0.001 462 s,0.002 166 s,0.003 893 s,1.963 615 s,各占大约0.07%,0.14%,0.21%,0.58%。可以看出其中SVD和谱峰搜索占了大部分的计算时间。本文着重进行SVD和谱峰搜索部分的优化,以提高计算效率。 2.1.1 接收数据 宽带信号与窄带信号[5]是一个相对概念,不同系统中的宽带信号与窄带信号具有不同的区分标准,且宽带信号与窄带信号的处理方法也有较大差距。 窄带信号是指信号带宽远远小于信号波前跨越阵列最大口径所需要的时间的倒数,即: (8) 式中:L为阵列最大口径;F和λ为信号中心频率和该频率对应的波长。 2.1.2 奇异值分解 基于单边Jacobi[6]旋转的SVD算法,相对于双边、单边的计算量小,并且容易并行实现。单边Jacobi方法直接对原矩阵A进行单边正交旋转,A可以是任意矩阵。AJ1J2…JK=B,同样每一轮的迭代都要使A的任意两列都正交一次,迭代退出的条件是B的任意两列都正交。单边Jacobi旋转有这么一个性质:旋转前若‖ap‖>‖aq‖,则旋转后依然是‖ap‖>‖aq‖;反之亦然。把矩阵B每列的模长提取出来,B=U·Σ,把J1J2J3…Jk记为V,则A=V·Σ·VT。 2.1.3 谱峰搜索 应用于MUSIC算法的谱峰搜索方法多种多样,主要有栅格化多细粒度搜索,应用于特殊阵列的免搜索或快速搜索算法,以及最优化求解的智能优化算法。根据系统资源与实现需求的不同,谱峰搜索的选择也不尽相同[5]。 由于本文系统的实时性要求较高,选取了三级细粒度直接搜索的方法。分别采用5°,1°,0.25°对全方位,一级点[-10°,10°],二级点[-2°,2°]作为栅格大小,如图4所示。 图4 常用谱峰搜索方法 为了高效实现MUSIC算法,将MUSIC算法中部分复杂运算放在GPU下去实现,GPU可以提供数十倍乃至于上百倍CPU的性能,将接收信号的模型、协方差的计算、SVD放入GPU里去并行计算,能够明显提升运行的速度。 为了提高复数SVD的计算效率,将获取列范数,归并排序,矩阵排序,单边Jacobi以及奇异值的排序放在GPU里去进行并行计算。CPU与GPU上的运行时间对比如图5所示。 图5 CPU与GPU上的运行时间对比 由图5可以看出,在GPU里的运行时间最终稳定在0.00 255 s,与原先在CPU里的运行时间0.003 893 s相比速度明显加快。 下面在谱峰搜索部分GPU的实现中进行了使用共享内存、分配锁页内存和增加CUDA流操作3个方面的优化。 首先将信噪比、中心频率、带宽、采样频率、采样时间、快拍持续时间、频率变化率设置为全局变量,减少大量的内存获取请求,从而减少时间的交互。 然后再将谱峰搜索中的计数器设置为共享内存,在调用过程中便不需要进行繁琐的交换数据。并且将调用__syncthread()函数来完成线程同步,这个函数的调用将确保线程块中的每个线程都执行完__syncthreads()前面的语句,才会执行下一条语句。这样可以确保对共享内存进行读取之前,想要写入的操作已经完成。优化前后的时间对比如图6所示。 图6 GPU上使用共享内存前后的时间对比 从图6可以看出,没有使用共享内存时,GPU的时间稳定在350 ms左右,使用共享内存后时间稳定在315 ms左右,有了执行时间降低了35 ms左右,性能提升10%左右。 PCI-E数据总线传输的数据始终是锁页内存中的数据,若应用程序没有对锁页内存进行分配,则CUDA驱动会在后台为程序分配。这之间必然存在分页内存与锁页内存中不必要的拷贝操作,所以,通过分配锁页内存来减少这些拷贝操作,提高效率[8]。 在应用程序中,将主机端分配内存的代码块: double*host_n=(double *)malloc(size_of_n_in_bytes); 替换为: double *host; CUDA_CALL(cudaMallocHost(&host_n,size_of_n_in_bytes)); 并将最后释放内存的代码: Free(host_n); 替换为: CUDA_CALL(host_n)。 测试运行时间,仿真结果如图7所示。 图7 GPU上分页内存与锁存内存的时间对比 从图7可以看出,使用分页内存时运行时间稳定在315 ms,使用锁页内存时稳定在310 ms左右,时间减少5 ms,性能上提升了1.6%,提升的空间并没有前面使用的共享内存优化那么明显。 CUDA流[8]表示一个GPU操作队列,并且该队列中的操作将以指定的顺序执行。我们可以在流中添加一些操作,如核函数启动、内存复制等。将这些操作添加到流的顺序也就是他们的执行顺序。将每个流视为GPU上的一个任务,并且这些任务可以并行执行。 首先是创建一个流: cudaStream_t aes_async_stream; CUDA_CALL(cudaStreamCreate(&aes_async_stream)); 相对应地会有销毁流: CUDA_CALL(cudaSteamDestroy(aes_async_stream)); 然后将需要的事件压入流中: CUDA_CALL(cudaEventRecord(start_time,aes_async_stream)); CUDA_CALL(cudaMemcpyAsync(dev_xt,host_xt,size_of_xt_in_bytes,cudaMemcpyHostToDevice,aes_async_stream)); 运行时间如图8所示。 图8 GPU上使用CUDA流前后的时间对比 从图8可以看出,在没有使用CUDA流之前,时间稳定在310 ms左右,使用CUDA流之后,时间稳定在284 ms左右,时间减少26 ms,性能上提升9.15%。 本文针对MUSIC算法的高效GPU实现,经过复数SVD的GPU并行计算,在谱峰搜索部分GPU实现中使用共享内存、分配锁页内存、增加CUDA流操作等几个方面的改进,整个计算过程减少56 ms的时间。总的来说,性能提升了20%的效率。实验结果表明,性能的提升能够符合预想的结果。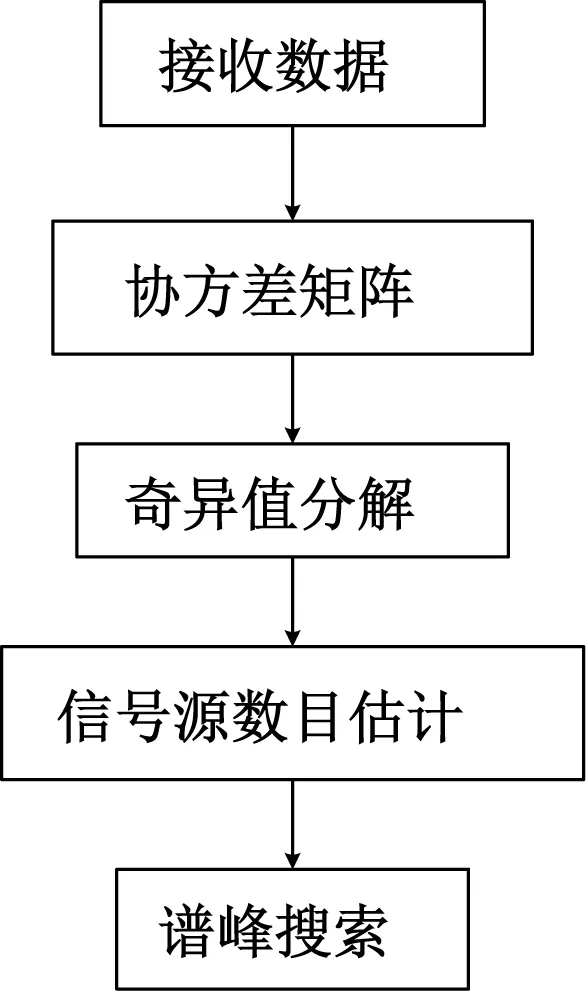
1.2 算法运行时间资源分配

2 使用GPU提升MUSIC算法运算效率
2.1 MUSIC算法分解

2.2 算法的GPU高效实现
3 算法仿真
3.1 改进SVD


3.2 使用共享内存
3.3 分配锁页内存
3.4 增加CUDA流操作

4 结束语

