时变时滞系统的L-K泛函

孙 欣, 高 跃

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

0 引 言

时滞系统的分析和综合一直以来是控制理论和控制工程领域研究的热点问题。自20世纪70年代 Lyapunov泛函引入时滞系统的分析设计以来,Lyapunov方法已经成为处理时滞系统的有利工具。基于Lyapunov稳定性理论,构造一个适合的Lyapunov-Krasovskii泛函(简称L-K泛函)得到时滞系统稳定性条件是分析和综合时滞系统常采用的方法。

一般地,由构造的L-K泛函得到的是时滞系统稳定的充分条件。目前,L-K泛函仍没有统一的构造方法。在构造L-K泛函时,通常含有积分项,从一重积分、二重积分逐渐发展为三重积分和四重积分。2010年,SUN等[1]提出将三重积分加入到L-K泛函中,有效降低了保守性。

同时, 因对积分项的放大而利用的不等式随之增多,形式不一。Xia 等[2]、孙等[3]文献中,积分项的放大均采用了Jensen积分不等式。文献[4]提出了Wirtinger积分不等式在时滞系统中的应用,相比Jensen积分不等式,Wirtinger积分不等式具有更小的保守性。

本文在对现有时滞系统研究成果的基础上,对L-K泛函的构造形式、L-K泛函求导后积分项处理这2方面做以分类、对比与总结。

1 构造L-K泛函

在稳定性判据推导过程中,需要构造一个合适的L-K泛函来获得系统稳定性条件。对于同一个时滞系统, L-K泛函的选取也不相同,因此得到的稳定性判据形式不同,结果的保守性也有差异。本文将针对时变时滞系统常用的3类泛函进行研究。

1.1 问题描述

考虑时变时滞系统

(1)

1.2 3类常用的L-K泛函

对于时滞系统而言,常用的L-K泛函包括双重积分型、三重积分型、四重积分型和增广型。

1.2.1 双重积分型L-K泛函

文献[5]针对区间时变时滞系统,选取了如下形式的L-K泛函:

其中:Qi>0,Wi>0,R>0,P,Qi,Wi,(i=1,2),R为正定矩阵;x(t)是为状态向量。 由式(2)可以看出,V3(t)为双重积分型, 对V3(t)关于t求导,得

(3)

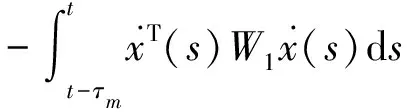
1.2.2 多重积分型L-K泛函

针对双重积分型 L-K泛函时滞信息有限的问题,现已扩展到多重积分型,其中包括三重积分型和四重积分型。

1) 三重积分型L-K泛函

文献[1]提出将三重积分加入到L-K泛函中,文献[6-8]在 L-K 泛函中也加入了三重积分项,形式如下:

(4)

其中Ui>0(i=1,2)为正定矩阵。

2) 四重积分型L-K泛函

文献[9] 在L-K泛函中加入四重积分, 具体形式如下:

(5)

其中Zi>0(i=1,2)为正定矩阵。

1.2.3 增广型L-K泛函

文献[3]在构造L-K泛函时,对状态向量进行扩维,得到增广型。形式如下:

V(t)=V1(t)+V2(t)+V3(t)+V4(t)

其中

(6)

其中:R,T,Q>0为正定矩阵;P为非奇异矩阵;Y为适维矩阵。

这里V4(t)状态向量是增广型。分别对V3,V4关于t求导,得

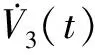
1.3 L-K泛函中时滞信息的处理

在推导时变时滞系统稳定性条件,构造L-K泛函时,通常要考虑时变时滞上下界τM,τm信息,不仅如此,还将时变时滞τ(t)的变化区间[τm,τM]分割成N(N≥2)部分,这种处理方法称为时滞分割法。根据情况,时滞可以进行均等分割,若考虑一般化情况,时滞还可以进行不均等分割。

1.3.1 时滞均等分割

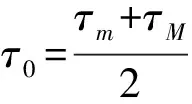
其中

其中:Qi>0(i=1,…,4),Tj>0(j=1,2)为正定矩阵。

可以看到V函数中不仅含有时滞下限τm和时滞上限τM,还有中值τ0。取中值的目的在于构造L-K泛函时另外增加了时滞中值的信息, 降低结论保守性。

1.3.2 时滞不均等分割

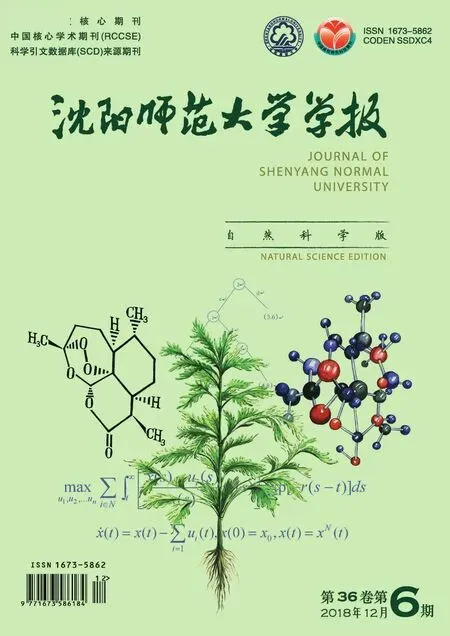
时滞不均等分割较均等分割更具一般性,可以利用更多时滞信息,降低结论保守性。以文献[9]为例,考虑时变时滞系统(1),运用时滞不均等分割方法构造L-K泛函。引入一个自由参数γ满足0<γ<1。变时滞h(t)满足hm≤h(t)≤hM,设hΔ=γhm+(1-γ)hM,则有hm

2 L-K泛函求导后积分项的处理方法

为了得到时滞系统稳定性条件,首先构造L-K泛函,然后对泛函求导。在求导过程中,为保证稳定性条件可以表示成线性矩阵不等式的形式, 方便利用MATLAB中LMI工具箱求解,需要处理L-K泛函求导后的某些积分项。或者进行恒等变形,例如引入自由权矩阵;或者进行放大,放大过程中,会选用不同形式的不等式,如Jensen积分不等式、Wirtinger积分不等式等。运用这些不等式时,相应会产生一定的保守性。

2.1 自由权矩阵方法

对泛函L-K求导后,可以通过增加矩阵变量构造恒为零的等式,以减少结论保守性,这种方法称为自由权矩阵方法。文献[5]中,添加了恒为零的等式:

自由权矩阵方法的优点在于,它没有改变原式大小,通过引入自由矩阵变量,降低结论保守性。

2.2 Jensen积分不等式

Gu等[10]提出了以下形式的Jensen积分不等式:对于向量函数x以及正定矩阵R>0,有积分不等式成立:

(7)

通过Jensen积分不等式,可以把不等式左边积分项含有的二次型转化成不等式右边2个向量相乘的形式,从而可以写成线性矩阵不等式的形式。还可以推广到二重积分或三重积分的情形。

(二重Jensen积分不等式)[11]:对于向量函数x以及正定矩阵R,以下积分不等式成立:

(8)

还有许多改进的Jensen积分不等式的运用,如文献[3,10-13]。

2.3 Wirtinger积分不等式

Wirtinger积分不等式是傅里叶分析中很著名的不等式,根据限定条件的不同,分为多种形式。与Jensen积分不等式相比,它具有更小的保守性。Wirtinger积分不等式的运用,可见文献[11,14-17];其离散形式的运用,可见文献[18-20]。

Wirtinger积分不等式[4]:对任意给定的常矩阵R>0,向量函数x:[a,b]→Rn,有如下不等式成立:

(9)

其中

(10)

注释2 比较式(7)、式(9),可以看到Wirtinger积分不等式比Jensen积分不等式保守性小。

Wirtinger积分不等式还有一些其它形式[11]:对任意的正定矩阵R>0,向量函数x:[a,b]→Rn,有如下不等式成立:

其中

Wirtinger积分不等式适用于连续时滞系统。与连续时滞系统对应的是离散时滞系统,那么离散型的Wirtinger不等式[18-19]可以应用到离散时滞系统中, 关于离散型的Wirtinger不等式有如下形式:

1) 对于给定的正定矩阵R>0,非负整数a,b,k满足a≤b≤k,x(s)为列向量函数,有如下不等式成立:

其中

其中

3 结 语

本文研究了时变时滞系统L-K泛函的构造和泛函求导后积分项的处理方法。L-K泛函包括双重积分型、多重积分型、增广型,以及利用时滞分割法构造L-K泛函。L-K泛函求导后积分项的处理方法,有自由权矩阵法、Jensen积分不等式和Wirtinger积分不等式方法。较Jensen积分不等式、Wirtinger积分不等式有更小的保守性。