含脉冲作用下连续切换系统的有限时间稳定
景 丽, 关胜楠
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
0 引 言
自20世纪60年代以来,现代控制理论已经在工业生产、军事科学以及航空航天等许多方面都取得了成功的应用。在1966年,文献[1]中首次提出了混杂状态连续时间动态系统,从此混杂动态系统成为了控制领域中的研究课题之一[2]。
近年来,从控制理论到控制工程对切换系统研究的兴趣不断提高。切换系统由一系列的连续子系统或离散子系统及作用在各个子系统之间的切换规则组成。切换系统有着广泛的实际背景,在各种控制系统中均有切换的存在,比较常见的有自动挡机动车控制系统、交通智能控制系统、大电网控制系统、火箭发射系统等[3]。
目前切换系统的成果很多,在稳定性方面主要考虑渐近稳定性。所谓渐进稳定是指在时间无穷的范围内从任意状态出发的运动都渐进收敛于原点。更需要研究系统在有限时间内的动态行为,即有限时间稳定。也就是指:在某一给定的时间间隔内,对于给定的系统初始状态,其状态轨迹始终保持某一给定的范围内。线性切换系统稳定性问题的分析主要应用统一Lyapunov函数、分段Lyapunov函数等方法进行。相关研究显示,如果线性切换系统的子系统渐进稳定,则子系统的状态矩阵可以互换,整个线性切换系统都是渐进稳定的。有限时间稳定比渐近稳定的研究更有优越性。
总的来说,目前国内外学者对切换系统围绕切换系统的建模、分析与控制3方面做了不同程度的较有意义的研究,其中切换系统各种稳定性分析与鲁棒控制是研究较多的问题之一。通过国内外学者做出的大量研究,基本形成一个初步的理论研究框架,但存在很多复杂问题尚待解决,比如目前对于切换线性系统稳定性分析的研究成果比较丰富,但切换非线性系统稳定性分析的研究依然比较少,尤其时滞切换非线性系统稳定性分析的研究成果就更少了。
在实际应用中,脉冲作用是不可避免的,这无疑恶化了系统的性能,甚至会导致系统的不稳定。对于脉冲系统的研究早在20世纪60年代V.D.Milinam和A.D.Myshkis就已经做过一些工作,之后又有学者们运用Lyapunov函数方法对脉冲系统进行了研究[4]。在外部脉冲的影响下,如何保证切换系统的稳定性并给出判定条件成为现有文献的重点研究内容。
脉冲系统和切换系统则因在诸如通讯网络、电力系统、机器人行走控制系统以及采样数字控制系统等中的广泛应用而得到大量关注。脉冲系统是指系统的状态瞬时发生变化,这种变化通常用状态跳跃来描述。典型的脉冲系统如:昆虫数量控制系统、化学作用系统、金融系统等。在电力系统等实际系统中,脉冲跳变和切换机制又时常同时存在[5]。关于非连续脉冲随机系统的稳定问题在文献[6]中被提出;文献[7]分析了不确定脉冲随机系统的采样鲁棒H∞滤波的问题。实际中还有这样的系统,当某些状态发生瞬时跳跃时,系统的结构也随之发生变化,如生命医学中研究如何有效控制某些传染病的流行,比较有效的方法是,在适当的时候给某些病人注射疫苗,以达到最佳控制效果,不同的接种率可能导致不同的控制结果。显然接种率是一个脉冲量。这样的系统称为切换的脉冲系统或具有脉冲作用的切换系统。在过去的十几年中,脉冲系统的发展极大地吸引了国内外学者们的研究兴趣[8]。
然而,具有状态跳变的切换系统的有限时间稳定的相关研究较少。例如文献[9]中给出了线性脉冲切换系统渐近稳定的充分条件,并且利用Laypunov直接法来设计一个能使脉冲切换系统鲁棒镇定的一个线性切换反馈控制器和一个脉冲反馈控制器。文献[10]中对脉冲切换系统的能控性和能观性做出了研究,文献[11]研究了脉冲切换系统的最优控制问题,以及带时滞的脉冲切换系统的稳定性的研究。因此,探讨具有脉冲作用的切换系统(连续切换系统、离散切换系统)的有限时间稳定就显得十分重要[12]。
本文主要分析含脉冲作用下连续系统的有限时间稳定性,应用Lyapunov稳定性理论,并运用MATLAB线性矩阵不等式等进行研究。
1 预备知识
给定一连续时间脉冲切换系统
定义1(切换系统的切换信号定义)[13]
对于任意给定的初始时间τ0及初始值x0,x0=x(τ0),与切换信号σ对应的切换序列:
s=x0(i0,τ0)(i1,τ1)(i2,τ2)…(ik,τk)…
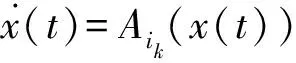
定义2(连续切换系统的有限时间稳定)
给定3个常数c1,c2,Tf(c1
引理1 给定适当维数的矩阵Y,D和E,其中Y是对称的,则Y+DFE+ETFTDT<0,对所有满足FTF≤I的矩阵F成立,当且仅当存在一个常数ε>0,使得Y+εDDT+ε-1ETE<0[14]。
引理2 对于任意一个n级实对称σ(t)矩阵A,都存在一个n级正交矩阵T,使TTAT=T-1AT成对角形。
2 主要结果
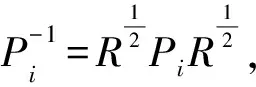
成立,那么系统是关于(c1,c2,Tf,R,σ)在脉冲作用下是有限时间稳定的。其中,Ei为脉冲矩阵,发生于子系统切换时刻。另外,
证明 选择如下形式的Lyapunov函数

F(t)沿着切换系统的轨迹对时间t求导,得
将上式在[tk,t]上进行积分得
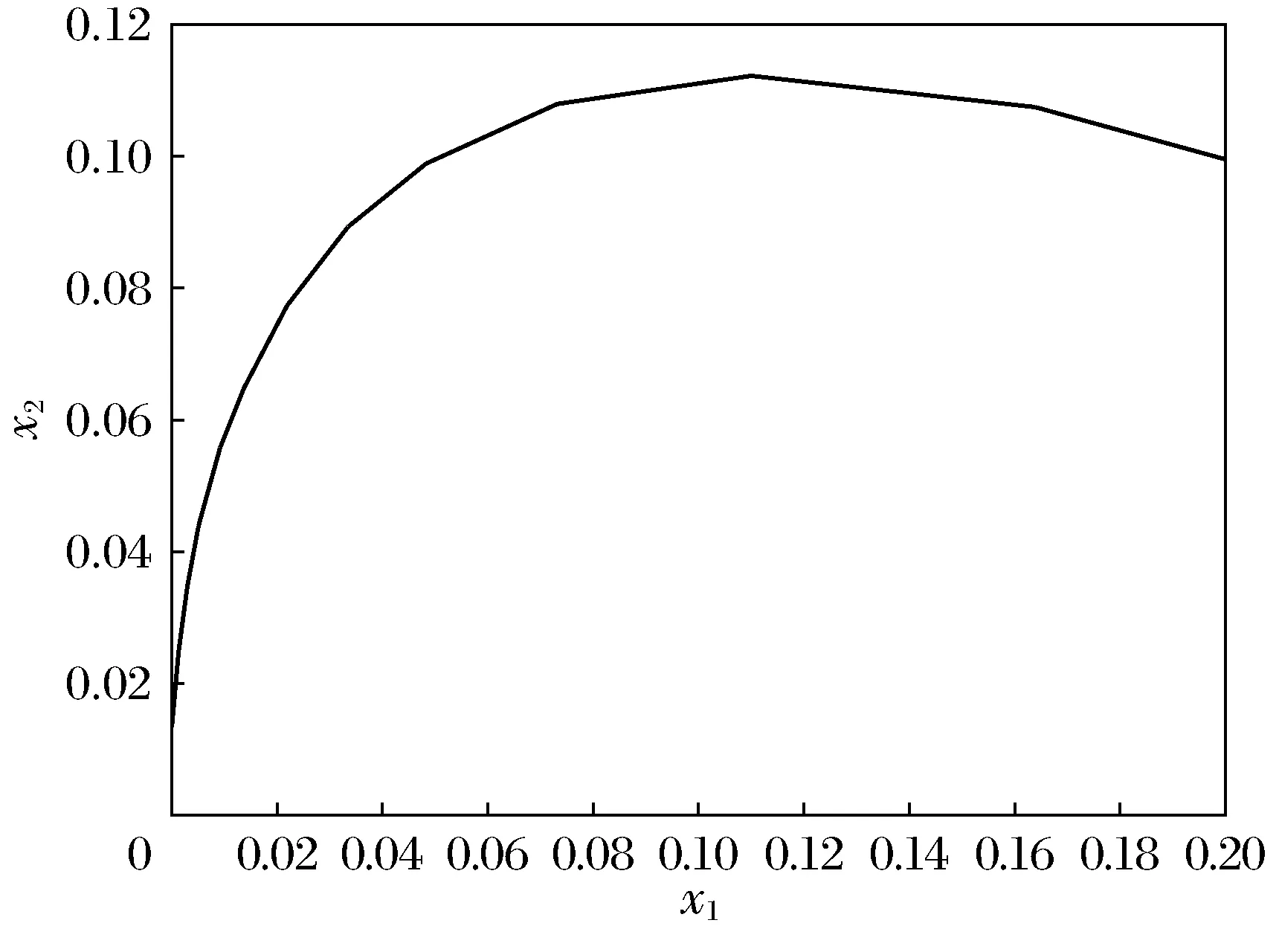
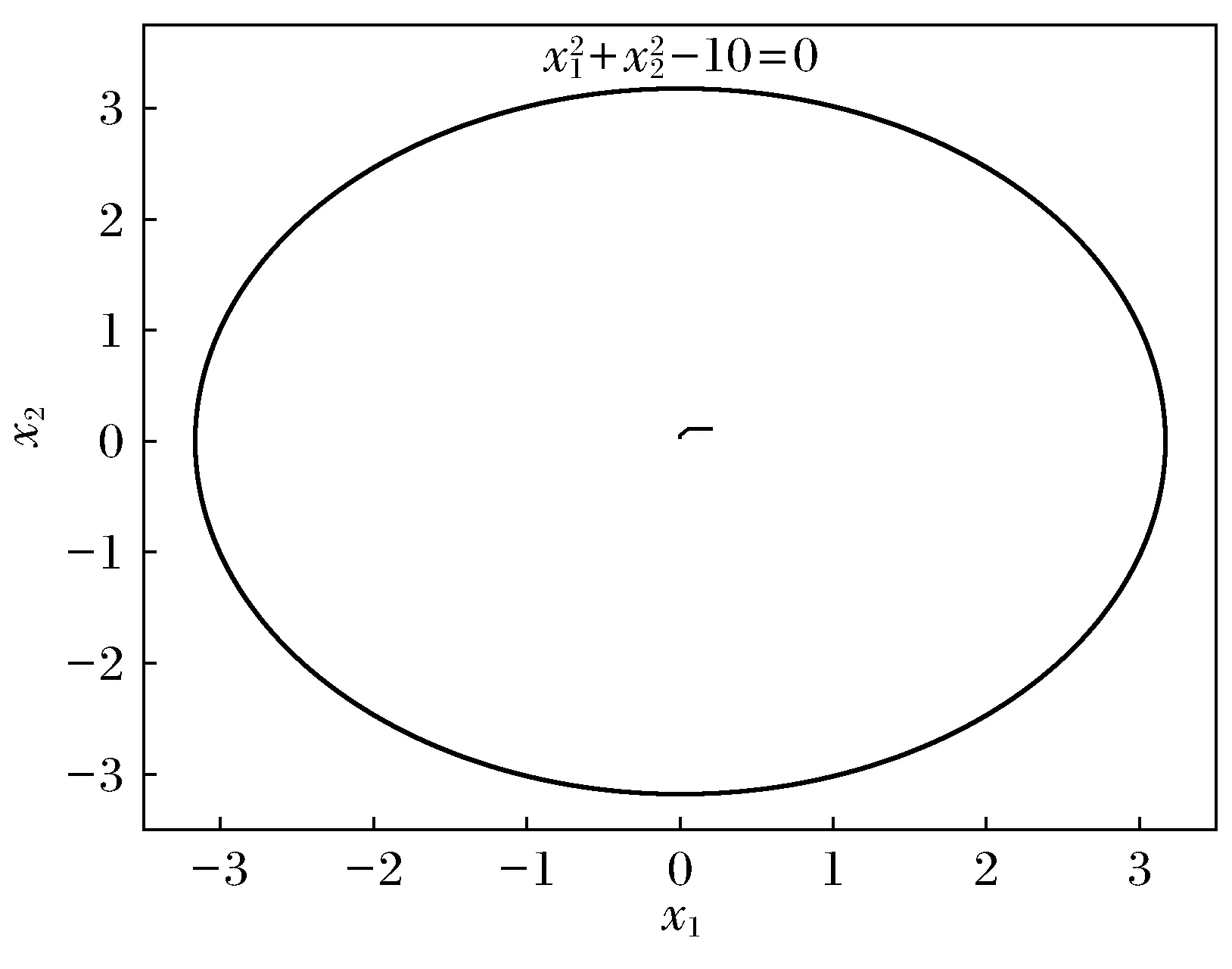
V(x(t))=Vσ(tk)(x(t)) 系统在切换时刻脉冲作用产生,当时刻t=tk时有 其中 (4) (5) 由引理2,可得 则式(5)可写为 则有 (6) 其中 重复上述过程,可以推出 当t=tk-1时, 当t=tk时, 因为V(x(t)) 所以 又因为 重复上述过程,可以推出 V(x(t))<(b′)k+1eα(t-t0)V(x(t0))=(b′)k+1eαTfV(x(t0)) (7) 可得Pi≥λ1I,Pi≤λ2I。从而有 结合式(7)~式(9)及xT(0)Rx(0)≤c1,可得 证毕。 考虑连续时间切换系统,其参数为 仿真参数选择如下: c1=0.1,c2=10,Tf=50,α=0.01,ε=0.1 由定理可求出系统切换的平均驻留时间τa=41.975 5 s。设初始条件为(x1,x2)=(0.2,0.1),应用MATLAB软件进行仿真,得到切换系统的相轨迹(图1)及切换系统有限时间稳定(图2),由2图可以看出相应的系统是有限时间稳定的。 图1 切换系统的相轨迹Fig.1 Phase trajectories of switched systems 图2 切换系统有限时间稳定Fig.2 Finite time stabilization of switched systems 本文研究了在含脉冲作用下连续时间切换系统的有限时间稳定性的问题[16],利用构造V函数和平均驻留时间方法得到了在脉冲影响下,系统仍是有限时间稳定的充分条件。以本文的方法为基础,可以研究含脉冲作用离散时间切换系统有限时间稳定的问题。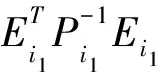
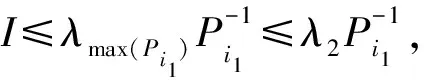
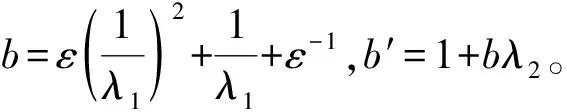
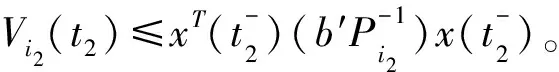
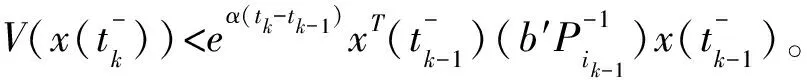
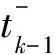
3 数值仿真
4 结 论