基于拆量思想的两轮逆向拍卖机制设计

王 娜, 汪定伟, 王洪峰, 王晓梅

(1. 沈阳师范大学 计算机与数学基础教学部, 沈阳 110034;2. 东北大学 信息科学与工程学院, 沈阳 110819)

0 引 言

制造行业企业原材料和服务的采购成本占到了总成本的50%～80%[1-4]。而逆向拍卖,尤其是网上逆向拍卖能够节约采购成本,缩短采购周期[5-8]。现在许多大中型企业都利用网上逆向拍卖来采购所需的原材料或服务[9-10]。

学者们对采购问题进行了大量的研究。Chen[11]讨论了一个买方和多个潜在供应商的采购问题。Li和Scheller-Wolf[12]考虑不确定需求的一个买方通过在线采购拍卖以降价方式从多个供应商处采购,比较了唯价格的推拉式合同拍卖,确定了拍卖设计和合同设计在采购拍卖中的相对重要性。刘树人等[13]研究了价格相依随机需求下零售商的逆向拍卖采购与定价联合决策问题。

大型企业集团在集中采购煤炭、石油和天然气等物资时,其总采购量通常会远远超过单个供应商的供应能力,这就需要多个供应商同时获得供应合同,将其称之为可拆分单物品的采购问题。

当标的物可拆分且单一种类,竞价人投标时需要标明单位价格和供应量等信息,拍卖人在保证总采购量满足要求的情况下,按照总采购成本最小或者采购单价最低的原则确定胜出的竞价人。但在实践中容易产生如下问题:

1) 供应商自由投标的供应量之和可能会与预期采购量不匹配,从而造成可行解数量过少,很难形成有效的竞争;

2) 投标价格较低的供应商可能无法与其他供应商构成可行解,造成采购成本偏高。

上述2种情况都会影响拍卖人的采购效果,带来不必要的经济损失。受文献[14-15]中多轮拍卖思想的启发,本文提出一种基于拆量思想的两轮逆向拍卖机制,其基本思想是:根据竞价人的第一轮标书中的投标单价和供应量,计算出竞价人在面对其他供应量时的期望投标单价,按照收益最大化原则确定期望投标策略,之后以拍卖商期望采购成本最小化为目标将总采购量拆分成若干个分量;在第二轮投标中,拍卖人仅允许竞价人对拆量包投标,根据实际投标情况,按照采购成本最小化原则确定最终胜标的竞价人。

通过实例计算与分析,表明这种基于拆量思想的两轮逆向拍卖机制对于这类可拆分单物品的集中采购问题是有效的。

1 拆量优化问题

拆量优化问题的目标是将总采购量拆分成若干个采购方案,即确定每个方案中的采购量,以获得最优的采购效益。为了对总采购量进行有效拆分,首先对竞价人的投标策略进行分析。

1.1 竞价人投标策略

首先给出竞价人投标策略的基本假设:

1) 竞价人都是风险中性的;

2) 竞价人供货的产品差异很小,近似认为产品是同质的;

3) 竞价人仅知道自己的单位成本;

4) 竞价人假设其他竞价人的单位成本是在行业水平的最低成本和最高成本之间均匀分布的独立随机变量;

5) 竞价人的投标策略都是相同的;

6) 竞价人的投标单价是其单位成本的严格单调递增函数;

7) 竞价人在自由投标情形下总是以最优供应量作为投标的供应量;

8) 各个竞价人之间无合谋行为;

9) 不止一个最低报价是小概率事件,可以认为不可能发生。

在上述假设前提下,分2种不同情形对竞价人投标策略进行分析。

1.1.1 自由投标情形下的竞价人投标策略

在自由投标情况下,竞价人不知道拍卖人的具体供应量信息,完全根据自己的供应能力进行投标,也即是竞价人在第一轮的投标过程。

令竞价人i∈N(i=1,2,…,n)的单位成本为ci,投标单价为pi。这里假设竞价人i的投标单价pi是单位成本ci的线性递增函数,表达如下:

pi=a+e·ci(e>0)

(1)

其中,a和e都是常数。

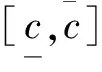
于是,在自由投标情况下,竞价人i报价低于其他竞价人报价的概率为:

(2)

于是,竞价人的单位期望收益ui可以计算如下:

(3)

令

得

(4)

又由式(1)pi=a+e·ci,可得

于是,在自由投标情形下竞价人i的投标策略为:

(5)

竞价人i可以根据其单位成本计算使其单位收益最大的投标单价,进而根据自身的供应能力确定最优供应量qi。

另一方面,一旦拍卖人了解到某一竞价人的投标单价,也能够获得该竞价人在供应量为qi时的单位成本ci,即

(6)

1.1.2 给定采购量情形下的竞价人期望投标策略

在非自由投标情形下,也就是当拍卖人公布一个采购量为g的采购方案或者拆量包时,竞价人报价时将不得不面对g不等于其最优供应量的情况,此时竞价人的单位成本将会发生变化。

根据经济学原理,当供应量为最优时,边际成本为0;当供应量小于最优供应量时,边际成本会随着供应量的增加而减小;当供应量大于最优供应量时,边际成本会随着供应量的增加而增大。假设最优供应量为q,此时单位成本为c0,当供应量为g时,单位成本c可以计算如下:

(7)

其中,β1和β2为2个非负参数。

参数β1用来刻画当供应量小于最优供应量时边际成本的变化程度。β1的值越大,则表示实际供应量g越低于最优供应量q时,边际成本变化越缓慢。当β1的值足够大时,边际成本几乎为0。对于某一竞价人来说,当拍卖人公布的采购方案或者拆量包小于其第一轮投标的供应量时,由于单位成本增加比较小,其博弈投标报价的变化也不会大。反之,β1的值减小,则表示随着实际供应量的减少,其边际成本提高越快,从而导致其博弈投标报价上升越快。一般来说,β1可取1.17。

参数β2用来刻画供应量大于最优供应量时边际成本的变化程度。β2的值越大,则表示实际供应量g越高于最优供应量q时,边际成本变化越缓慢。当β2的值足够大时,边际成本几乎为0。对于某一竞价人来说,当拍卖人公布的采购方案或者拆量包大于其第一轮投标的供应量时,由于单位成本增加比较小,其博弈投标报价的变化也不会大。反之,β2的值减小,则表示随着实际供应量的增加,其单位成本增加较大,从而导致其博弈投标报价上升较大。一般来说,β2可取1.0。

设拍卖人公布一个给定供应量g,根据上述讨论,按以下步骤计算给定供应量下竞价人i的期望投标策略。

步骤PC:

Step 1 以竞价人i第一轮投标的供应量qi作为最优供应量,投标单价定义为pi(qi),投标单价与供应量之间具有函数关系;

Step 2 利用公式(6)计算出竞价人i在自由投标阶段供应量为qi时的单位成本ci(qi);

Step 3 利用公式(7)计算出竞价人i在给定供应量为g时的单位成本ci(g);

Step 4 利用公式(5)计算出竞价人i对这一采购方案的投标单价pi(g),考虑到竞价人的能力和意愿,规定竞价人i对供应量g:|g-q|≤[10%Q]投标,其中Q为总采购量;

Step 5 计算竞价人i的收益:ui(g)=[pi(g)-ci(g)]·g。

如果拍卖人公布m个给定供应量的采购方案G={g1,g2,…,gm},规定竞价人i只能对至多一个捆绑gk,k=1,2,…,m进行投标,此时按照以下原则确定竞价人i对G的投标策略:

最大收益原则:竞价人i选择ui(G)中最大收益进行报价。

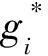
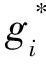
(8)

需要说明的是,这样的结论是拍卖人根据竞价人第一轮投标结果进行推导而得,并不是竞价人的真实投标行为,故本文将其称之为竞价人的期望投标策略。

1.2 拆量优化模型

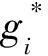
(9)

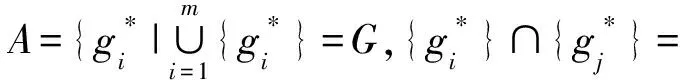
将拆量优化问题描述如下:

拍卖人根据n个竞价人第一轮投标结果,将总采购量Q拆分为m个采购方案G={g1,g2,…,gm},其中gmin≤gi≤gmax(i=1,2,…,m),gmin和gmax分别表示最小供应量和最大供应量,以获得最优的期望采购效益,即实现期望采购成本最小化。

需要说明的是,拆量方案的数目m将由拍卖人预先设定。拍卖人可以根据企业的具体情况,来确定m的值,以达到防止垄断的目的。

以采购效益最优为目标函数,以拆量方案的每个供应量为决策变量,建立拆量优化问题的数学模型,具体如下:

(10)

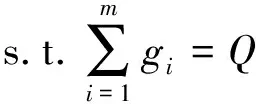
(11)

gmin≤gi≤gmax,i=1,2,…,m

(12)

目标函数(10)表示最小化拍卖人的期望采购成本,约束条件(11)表示所有拆量方案的供应量之和等于拍卖人的采购总量,约束条件(12)表示决策变量gi(i=1,2,…,m)的取值范围。

上述拆量优化模型中,决策变量是一组gi(i=1,2,…,m),约束条件均为线性的,且目标函数需要通过求解组合优化问题才能够计算出来。因此,上述模型是由线性规划与组合优化组成的混合优化问题,这种优化问题显然无法通过一般的数学规划方法求解。但遗传算法等可以方便的进行求解,限于篇幅,这里不对模型(10)—(12)的求解方法展开讨论。

2 基于拆量思想的两轮逆向拍卖机制设计

根据前面的讨论,提出基于拆量思想的两轮逆向拍卖机制,具体实施步骤如下:

Step 1 采购方在投标网站系统上发布采购信息,包括采购物品以及相应的最小供应量、最高采购价格和最低质量参数要求、供应商资质要求、采购流程具体要求等相关信息;

Step 2 采购方对所有表示投标意愿参加竞价的供应商进行资质验证,对合格的供应商发送加密的验证码,发起第一轮投标;

Step 3 验证合格的供应商进入投标系统,上载密封的标书,标书中需要标明物品的供应量、单价以及质量参数信息;

Step 4 采购方根据第一轮投标结果,按照步骤PC和最大收益原则计算出竞价人的期望投标策略,并按照模型(10)～(12)求解出最优拆量方案;

Step 5 在投标系统中公布新的采购方案,发起第二轮投标,规定供应商只能对方案中至多一个分量进行投标;

Step 6 具有验证码的供应商对新的采购方案再次进行投标,上载密封标书;

Step 7 采购方根据第二轮投标结果,按照采购成本最小化指标确定胜出的供应商,并与供应商签订供货项目协议。

3 实例计算与分析

通过大量数值实例,证明了以上基于拆量思想的两轮逆向拍卖机制的有效性。为描述方便,这里仅介绍一个小规模的例子。

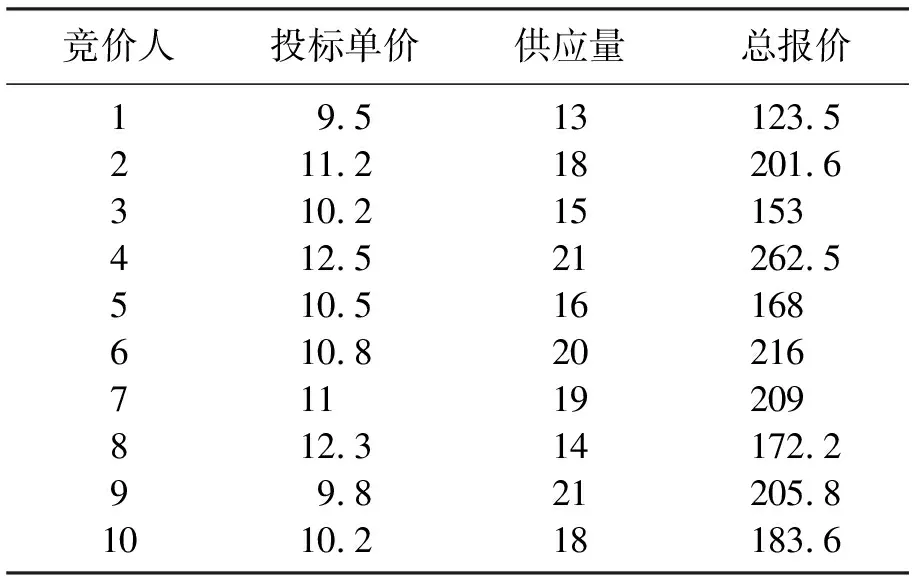
表1 竞价人第一轮的投标情况Tab.1 The bided data of first turn bidding

假设拍卖人对一种物品进行招标,期望的总采购量Q为35,采购上限为37,每个竞价人的供应上限和下限分别为25和10;有10个符合资质要求的竞价人参与投标,竞价人标书中投标单价和供应量如表1。

在传统单轮逆向拍卖下,为了达到总采购量,可以得到9个可行解,如:

可行解1:{2,7},采购量为:18+19=37>35,采购成本为:201.6+209=410.6;

可行解2:{3,9},采购量为:15+21=36>35,采购成本为:153+205.8=358.8;

可行解3:{5,6},采购量为:16+20=36>35,采购成本为:168+216=384;

……

注： 表中加粗的数字表示胜标者及其报价。

通过枚举法,最终求得可行解2为最优解,即竞价人3和竞价人9胜出,最后拍卖人的采购成本为358.8,采购量为36,比总采购量多出1个单位。另外,从投标结果来看,竞价人1的投标单价最低,但由于它无法与其他标书构成可行解,拍卖人不得不放弃。

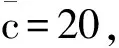
依据拆量优化模型,最优的拆量方案为

G={16,19}

分别由竞价人3和竞价人7的期望投标策略而获得,对应的期望投标单价分别为10.7467和11。

拍卖人第二轮按这2个分量重新招标,采购单价不高于12。第二轮投标情况见表2。

从表2可以看出,竞价人分别根据2个确定采购量16和19修改了自己的投标方案,组成的可行解数量由原来的9个上升为现在的24个。按照拍卖人采购成本最小化原则,很容易得到最优解,即胜标人为竞价人1和9,最优采购成本为344.9。这个价格比单轮逆向拍卖下的最优值358.8节省了3.8%。这个拆量的结果让原来出价较低的竞价人1也得到胜出的机会,显然取得了比较好的拍卖效益。

4 结 语

政府和大型企业集团在集中采购煤炭、石油等物资时通常采用将采购量拆分的逆向拍卖方式,但是一方面供应商自由投标的供应量之和可能会与预期采购量不匹配,从而造成可行解数量过少;另一方面投标价格较低的供应商由于无法与其他供应商构成可行解,也使得拍卖人不得不放弃。本文提出了一种基于拆量思想的两轮逆向拍卖机制。首先根据竞价人第一轮自由投标的结果按照收益最大化原则确定其投标策略,并以拍卖人期望采购成本最小化为目标确定拆量方案,再按拆量方案进行第二轮投标。这种拍卖机制使得可行解数量大大增加,从而激化竞争,取得更好的拍卖效果。