基于逐步回归的稳健估计和异常值检测

崔 乐, 吴 迪, 成丽波

(长春理工大学 理学院, 长春 130022)

0 引 言

近年来,异常值检测一直是统计诊断中一个比较活跃的研究课题。在实际生活中,由于种种原因不能够和其他数据一起用于多元统计的线性回归模型中的值,称为异常值。换句话说,参数估计、模型构建及预测都会受到异常值的影响,因此,这篇文章主要研究的是基于逐步回归的稳健估计和异常值的检测。

比较常见的统计量有残差、学生化残差、Cook距离以及W-K统计量等。残差和学生化残差[1-3]都可以用来检测异常值,但是残差没有考虑到异方差性,而学生化残差考虑到了这一点,因此用学生化残差检测异常值比用普通残差更有效。而Cook距离和W-K统计量[4-6]仅可以判断出数据是否有强影响点,但是异常点和强影响点之间没有必然的关系,即异常点不一定是强影响点,强影响点也不一定是异常点。

本文基于逐步回归模型,从残差平方和的角度出发,研究出检测异常值的方法,并估计异常值的大小。通过与传统方法的比较,验证该方法的有效性。

1 逐步回归

在多元线性回归模型中,自变量的选择实质上就是模型的选择。现设一切可供选择的变量是t个,它们组成的回归模型称为全模型(记m=t+1),在获得n组观测数据后,有模型

其中:Y是n×1的观测值,β是m×1未知参数向量,X是n×m结构矩阵,并假定X的秩为m。

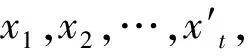
β=(βp,βq)′,X=(Xp⋮Xq)

下面从不同的角度给出自变量选择的准则[7]。

准则1 平均残差平方和达到最小

准则2CP统计量达到最小

该准则是由马斯洛于1964年从预测的角度提出:

准则3 AIC准则

该准则由日本统计学家赤池弘次于1974年根据极大似然估计原理提出:

AIC=nln(SSEP)+2P

其中:SSEm是m个自变量x1,x2,…,xm所对应的残差平方和;SSEP是p个自变量x1,x2,…,xp所对应的残差平方和。

快速选择变量的算法有很多,例如:向前法、向后法、逐步回归法[7]等,其中逐步回归法是应用最广的一种方法。它的具体做法是先将变量一个一个的引入,当引入到第3个变量之后的每一步,首先对已引入的变量进行剔除。这样,自变量将不断的引入、剔除、再引入、再剔除……直到自变量不能被剔除,同时也无法引入自变量为止。

2 基于逐步回归的残差平方和

经过逐步回归后生成最优多元线性回归模型如下:

yi=β0+β1xi1+β2xi2+…+βpxip+εi,i=1,2,…,n

(1)

其中:p为解释变量的数目;βj(j=0,1,…,p)为回归系数;εi为随机误差,且εi～N(0,σ2),i=1,2,…,n;β=(β0,β1,…βp)T;σ为未知参数。

均值漂移模型[8-9]是在第i个数据点上增加一个漂移项δ,即在这个数据点yi处的均值发生了非随机漂移,若δ显著不等于零,则yi处的均值发生了漂移,说明此点为异常点。

由于事先不知道在线性模型中出现异常值,因此,可以先假定模型中没有异常值,其线性模型的矩阵形式为

Y=Xβ+ε

(2)

其中

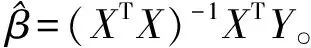
SSE=YT(I-H(X))Y

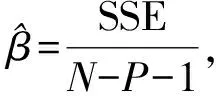
残差平方和(SSE)会受到异常值大小的影响,即随着异常值的增加,残差平方和(SSE)也增加。

3 异常值的检测

基于均值漂移模型,假设模型中的第i个观测值为异常值,即异常值的大小为δi,其余的皆为正常数据,计算此时的残差平方和(SSEi)为

(3)

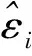
(4)

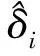
(5)

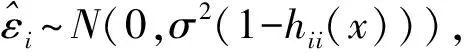
4 稳健估计和异常值的识别

4.1 标准差的稳健估计

M估计是基于最小二乘估计发展起来的一种抗差估计(Robust Estimation)方法[10-12],是由huber于1964年最先提出来的,也称为广义最大似然估计。M估计已经成为最经典的一种稳健估计方法。

M估计的估计方程写成矩阵形式是这样的:

XTWXβ=XTWY

(6)

迭代公式如下:

(7)

其中:W是以ωi,i=1,2,…,n为对角线的权矩阵;X是解释变量矩阵,X=(x1,x2,…,xn);Y是因变量向量,Y=(y1,y2,…yn)T。

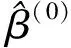
4.2 异常值的识别

5 模拟与实例分析

5.1 模拟实验

假设有一多元线性回归模型y=3+5x1-4x2+4x3-3x4+x5-2x6+2x7-x8+3x9+6x10+ε,现利用计算机模拟产生100个数据样本。下面考虑3种方案进行实验。

方案1 将大小为5.5的异常值加入到第49个样本观测值中。

方案2 将大小为6,-5的异常值分别加入到第31和69个样本观测值中。

方案3 将大小为-6.5, 5.5, 4.5, -3的异常值分别加入到第48～52个样本观测值中。

1) 异常值检测

对于3种方案的D统计量如图1所示。图1是基于M估计的D统计量,由图1(a)可以看出,第50个观测值对应的D统计量远大于3,判定为异常值。同样由图1(b)可以看出,第32个和第70个观测值为异常值;由图1(c)或者看出,从第49～53个观测值均被检测出异常值。由此可以看出该检测异常值的统计量可以很好地检测出异常值,并且由于方案3是5个连续的异常值,因此说明此方法对异常值的遮蔽现象有一定的作用,能够有效地检测出连续几个异常值。

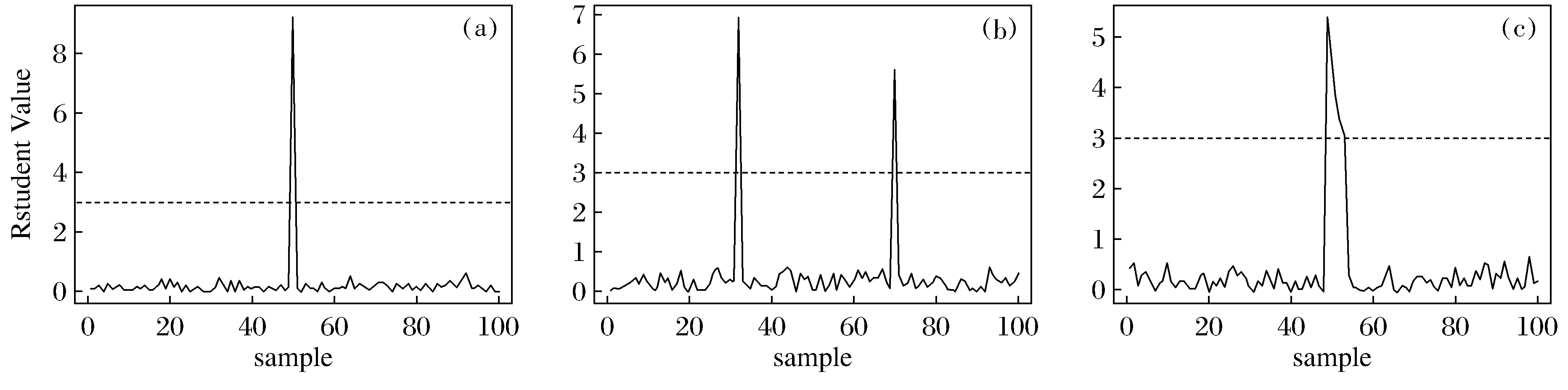
图1 方案1～3的基于M估计的D统计量Fig.1 D Statistics Based on M Estimation for Schemes 1～3

图2是方案1～3中每个样本观测值的学生化残差示意图。按照传统的方法,将观测值的学生化残差的绝对值大于3的认为是异常值。从图2(a)中可以看出,无法准确地检测出方案1中异常值,图2(b)中,可以很好地检测出方案2中的异常值,从图2(c)中,学生化残差只能检测出第49, 50, 52, 53个观测值为异常值。由此可以说明,用新构建的基于稳健估计的D统计量比传统的学生化残差检测异常值更加有效。

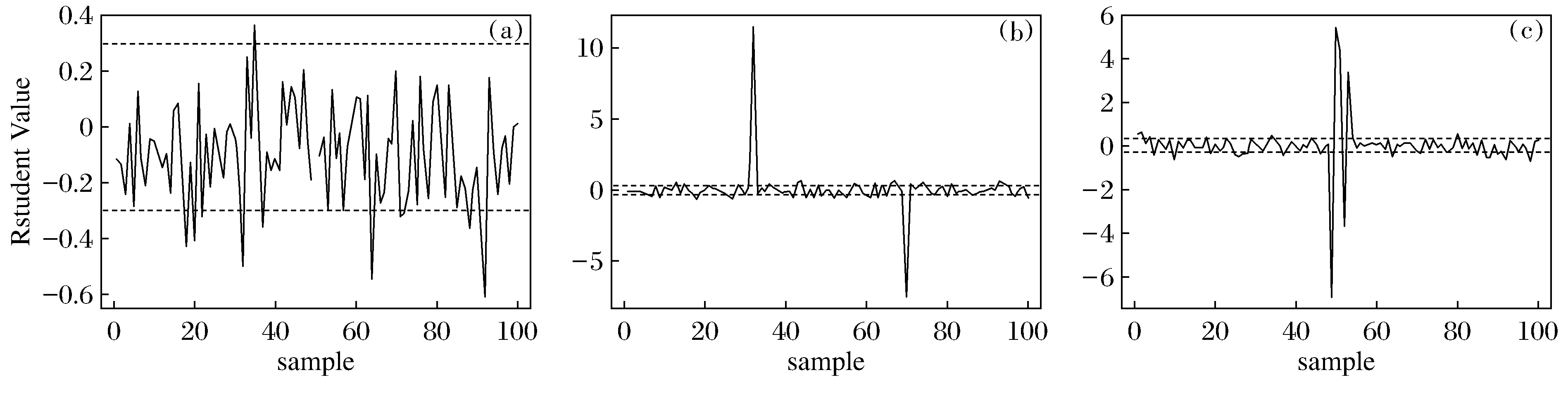
图2 方案1～3的学生化残差Fig.2 Student Residual in Scheme 1～3

2) 异常值大小的估计

通过公式(4)来计算异常值的大小,表1是3种不同方案的异常值大小的评估值。从表中可以看出,对于方案1～2,本文构建的统计量都可以很好地检测出异常值的大小。对于方案3异常值大小估计精确度不如方案1～2,但仍然还是比较准确的。

表1 基于方案1～3的异常值大小估计值Tab.1 Outlier size estimates based on Schemes 1～3

5.2 实例分析

在房地产行业中,影响房屋价值的因素有很多。本实例中,根据房屋价值的影响因素及人们的偏好,记录的影响房屋价值的指标包括面积、户型、当前楼层、总楼层、朝向、装修情况。其中,户型为几室几厅,可以分开作为单独变量;当前楼层分为底层、中层和高层;朝向分为北、东北、东、东南、南、西南、南北、西、西北、东西;装修情况分为毛坯、普通装修、精装修。

房价和房屋面积需要以10为底取对数,目的是降低房价和面积的数量级,提高模型估计精度。户型是一个连续的数值变量,可以不用修改。其他的字符型变量则需要进行量化。楼层包括3种,根据计量经济学知识,本方案将采用2个0-1变量(构成一个二维行向量)度量该3种类型。例如,(0,0)代表低层,(1,0)代表中层,(0,1)代表高层。其他分类指标同样需要进行类似处理。本文选取河北省邯郸市某小区的样本数据。

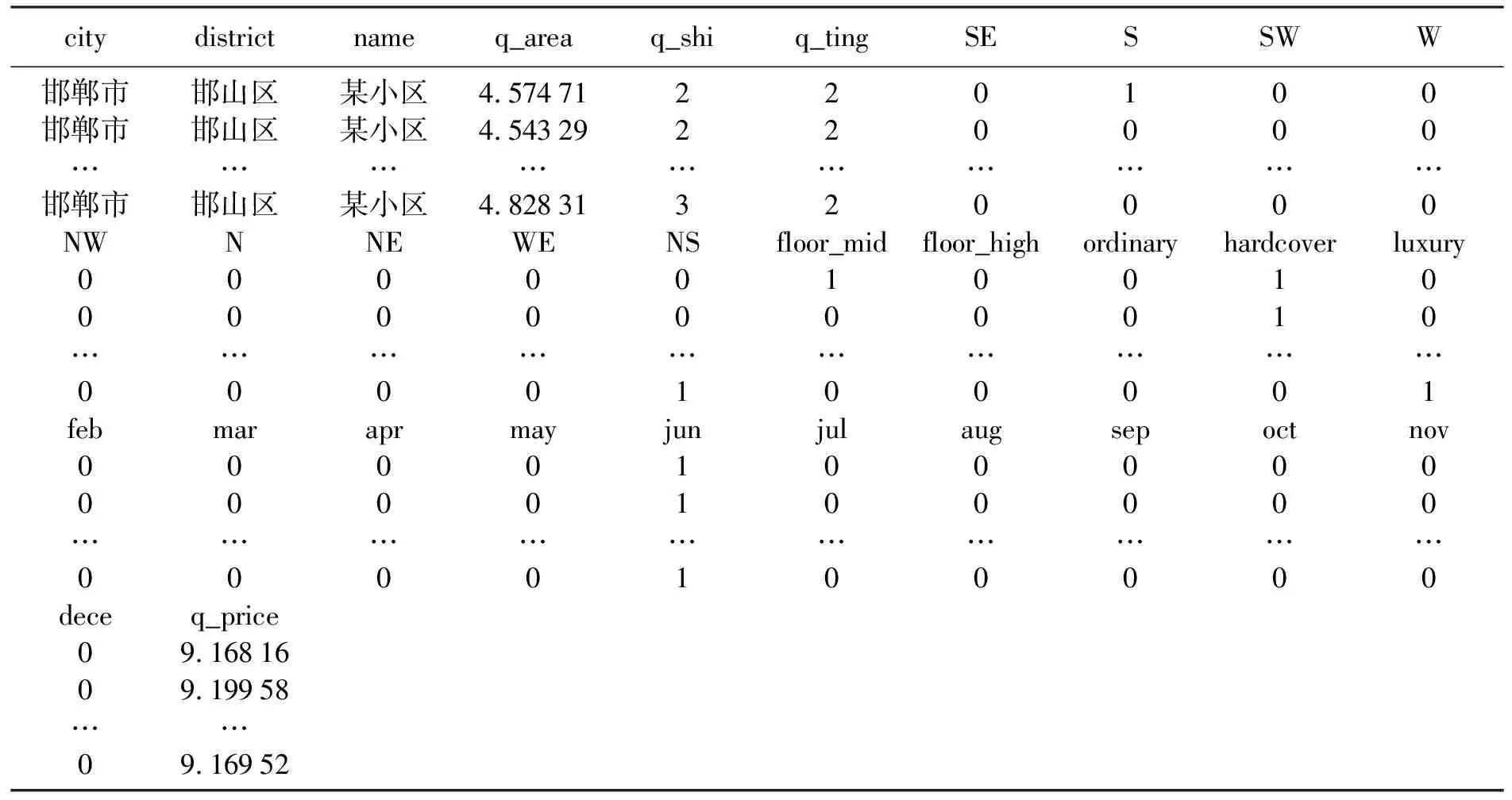
表2 河北省邯郸市某小区的样本数据Tab.2 Sample data of a residential district in Handan city, Hebei province

该实例的线性回归模型为

经过逐步回归之后所得到的“最优”回归模型为

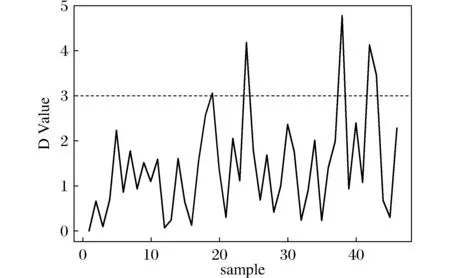
图3 基于M估计的D统计量Fig.3 D StatisticsbBased on M estimation

1) 异常值检测

从图3可以看出,第24,38,42,43个样本的对应的D统计量大于3,可判断为异常值,其中虽然第42和43的样本连续异常,但仍然能够被很好地检测出来,再一次证明此方法对异常值的遮蔽现象有一定的作用,能够有效地将连续几个异常值检测出来。

2) 异常值大小的估计

同样,由公式(4)估计出异常值的大小,估计结果如表3所示。

表3 异常值大小的估计值Tab.3 Estimates of the size of outliers

6 结 语

异常值检测是当前数据分析研究中的一个热点问题。通过大量的模拟实验和实例分析,得到这样的结论:基于M估计的D统计量可以很好地检测出异常值,尤其是对异常值的遮蔽现象有一定的作用----能够有效地检测出连续的几个异常值。