异步切换下一类线性时变时滞系统的鲁棒控制
刘玉忠, 张嘉恬
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
0 引 言
切换系统是一类重要的混杂系统,它由有限个子系统及作用在其中的切换规则组成,由于切换系统具有非常重要的实际意义,在过去几十年中被普遍关注[1-17]。WICKS等[3]研究了共同李雅普诺夫函数方法;BRABICKY[4]和孙常春等[5]研究了多李雅普诺夫函数方法;HESPANHA等[6]研究了基于驻留时间的慢切换方法。平均驻留时间方法作为研究系统稳定性的重要方法,要求在有限时间内切换次数是有限的,并且在2个连续切换点间的时间间隔的平均值不小于一个常数,学者们发现在相关稳定性分析中,平均驻留时间切换比驻留时间切换的保守性要小[7-9]。
在切换系统中,把一个子系统称为一个模型,而本文所说的控制问题就是设计模型依赖控制器或模型独立控制器并找到可行的切换信号使系统稳定[10-11]。模型依赖的控制器具有更小保守性,这就意味着控制器间的切换与模型间的切换完全同步的实际意义很小。异步控制是指备选控制器间的切换与系统模型间的切换是异步的,因为在实际中控制器需要时间去识别系统模型,这就使控制器与系统模型之间无法完全同步,即产生了控制器的延迟。由于异步控制在实际生活中具有重要研究价值,因此许多研究领域都涉及到了异步切换,例如异步观测器设计[12]、异步滤波[13]、异步H∞控制[14]等。Zhang和Gao[15]研究了线性切换系统的异步切换;Lian和Ge[16]研究了异步切换下切换系统鲁棒H∞输出跟踪反馈问题;Fei等[17]研究了2-D切换系统的异步控制问题。虽然考虑带有时滞以及不确定的切换系统会使分析变得更加复杂,但却具有实际意义。
本文研究了在异步切换下含有不确定时变时滞系统的鲁棒控制问题。首先利用平均驻留时间方法得到了异步切换下系统指数稳定的充分条件,其次在此基础上设计了相应的状态反馈控制器,用Schur补引理将其转化为线性矩阵不等式便于利用MATLAB等数学工具求解。
1 问题描述
考虑由以下状态方程描述的不确定时变时滞系统:
(1)
式中:x(t)∈Rn是状态向量;u(t)∈Rm是控制输入;A、B、D、E1、E2、Ed是已知的适当维数矩阵;ΔA、ΔAd、ΔB是范数有界不确定参数矩阵且满足[ΔAΔAdΔB]=DF(t)[E1EdE2],其中F(t)∈Ri×j为满足FT(t)F(t)≤I的不确定矩阵;σ(t)是时间的分段常函数,称为切换信号,σ(t):[0,∞)→M={1,2,…,t},l为子系统个数,与之对应的一个切换序列可记为0 0≤d(t)≤h,d(t)≤τ<1 (2) 构造一个无记忆状态反馈控制器 u(t)=Kσ′(t)x(t) (3) 结合式(1)和式(3)所导出的闭环系统如下: (4) 本文目的是得到系统(4)鲁棒指数稳定的充分条件以及得到状态反馈控制器的控制器增益矩阵。为此需要下面的引理。 引理[18]给定适当维数的矩阵Y、D、E,其中Y是对称的,则 Y+DFE+ETFTDT<0 对所有满足DT(t)F(t)≤I成立,当且仅当存在一个常数ε>0,使得 Y+εDDT+ε-1ETE<0 定理1 给定常数α>0,β>0,∀i,j∈M,i≠j,如果存在对称正定矩阵Pj,Ri和常数ε1>0,ε2>0,使 Pi≤μPj,Ri≤μRj (5) (6) (7) 成立,这里 假设子系统的驻留时间满足下式: (8) 则异步切换下切换系统(4)指数稳定。 证明 分别讨论t∈[tk-1+Δk-1,tk)和t∈[tk,tk+Δk)的情形。 1) 当t∈[tk-1+Δk-1,tk)时,构造分段Lyaponov泛函: (9) 由式(2)可得 (13) 由式(6),可得到 (14) 这里 2) 当t∈[tk,tk+Δk)时,构造分段Lyaponov泛函: 在此区间内σ′(t)=i,σ(t)=j (15) V2σ′(t)在此区间上的导数为 由定理1和式(7)可以得到 再由引理得,存在一个标量ε2>0,使 (18) 由式(18)得 (19) 结合式(14)和式(19)得 显然如果式(8)成立,则有t→∞时,V(t)→0。 令κ1=minλmin(Pi),κ2=maxλmax(Pi)+hmaxλmax(Pi),由式(23)可以得到 结论得证。 定理2 给定常数α>0,β>0,μ≥1,∀i,j∈M,i≠j,如果存在ε1,ε2,Xi>0,Vt>0,并且对任意矩阵Wi满足如下LMIs: 这里 证明 应用矩阵的Schur补引理,(6)式等价于 (28) 式(28)等价于 对上式矩阵分别左乘和右乘矩阵diag{Xi,Vi,I,I,I,I}可得式(26),同理对式(7)做相同的处理可得式(27)。 此外,应用Schur补引理,式(25)等价于 即由式(25)可得式(5)。 结论得证。 文章研究了一类不确定时变时滞线性切换系统的异步切换问题。通过平均驻留时间法,找到了保证切换系统在异步切换下鲁棒指数稳定的充分条件。构建的李雅普诺夫函数是控制器切换信号决定的并且选取的李雅普诺夫函数在控制器与系统模型的异步阶段是允许增长的。最后在获得相应保证其稳定的控制器增益过程中,得到了关于变量的线性矩阵不等式,这有利于在其可行时找到它的可行解。

2 主要结果


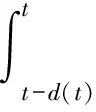
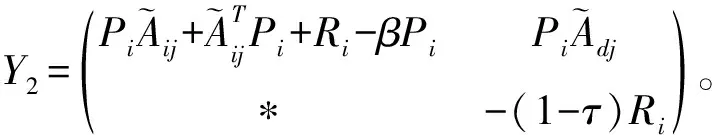
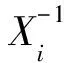


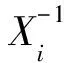
3 结 论