基于区间犹豫模糊TOPSIS法的多属性群决策
赵蒙川, 杨 雁, 向 毅
(1. 四川理工学院 数学与统计学院, 四川 自贡 643000; 2. 四川大学 商学院, 四川 成都 610011)
多属性群决策(MAGDM)问题是从含有多个属性的一组备选方案中,对所有备选方案排序并从中选取最优方案,广泛存在于各类社会生产活动中,如政治学、经济管理学、社会文化学、建筑学等.在群决策过程中,决策者根据主观认知和判断对每一方案的各个属性进行评价,如何将具有不同偏好的各个决策者的决策信息进行聚合,并得到一致性的结果,专家们进行了相关的研究[1-5].
由于模糊和不确定性现象广泛存在实际生活中,再加上人类认知水平及主观判断的局限性,造成决策信息不仅仅是以精确数的形式出现.为了准确描绘决策过程中的模糊不确定性,专家学者针对不同的语义环境相继提出了多种形式的模糊集.1965年,美国加利福尼亚大学控制论专家Zadeh[6]首次提出模糊集FS(Fuzzy Sets)的概念,模糊集合的出现使得数学的理论和方法能够处理模糊不确定性现象,至此以后模糊集理论发展迅速并成功应用于各个领域.受到人们认知水平的限制,常用区间数的形式描写决策信息.因此,1986年Turksen[7]提出了区间模糊集IVFS(Interval-Valued Fuzzy Sets)的理论,其隶属度都以区间数的形式出现.由于前述两类模糊集无法完整地表达决策信息,这样就造成了信息的丢失.为了克服信息丢失而造成决策结果的不准确的缺陷.Atanassov[8]在1986年提出直觉模糊集IFS(Intuitionistic Fuzzy Sets)的基本概念.引入隶属度、非隶属度和犹豫度表达决策的信息,该理论更加全面传达了决策者的主观意愿.1989年Atanassov等[9]将直觉模糊集推广到区间的形式,给出了区间直觉模糊集IVIFS(Interval-Valued IFS)的定义.多属性群决策问题其实是多名决策者对某一待评属性进行评价,如果遇到决策者们犹豫不决、优柔寡断,同时他们还无法说服彼此,将会造成最终的决策结果很难达成一致.于是,在2009年文献[10-11]提出了犹豫模糊集HFS(Hesitant Fuzzy Sets)的基本概念,其隶属度是由所有可能的值构成的集合.2013年,Chen等[12]在犹豫模糊集和区间模糊集的基础上,定义了区间犹豫模糊集IVHFS(Interval-Valued HFS),其隶属度是由所有可能的区间数构成的集合.
逼近理想解排序(TOPSIS)法[13]是最常用的多属性群决策方法.常规的TOPSIS方法[13-18]是用精确数、模糊数、区间数、直觉模糊数、区间直觉模糊数以及犹豫模糊元表示决策矩阵中的决策信息.但是,对于多属性群决策中以区间犹豫模糊元表示决策信息的情形,常规的TOPSIS方法不能有效地解决.为此,本文将TOPSIS法和区间犹豫模糊集相结合提出了区间犹豫模糊TOPSIS(IVHF-TOPSIS)法,用于解决属性评价值为区间犹豫模糊元的多属性群决策问题.
1 基本理论
定义1[12]令X为一给定的集合,D[0,1]表示区间[0,1]上的所有闭子区间组成的集合,则关于X的区间犹豫模糊集(IVHFS)为
A={〈xi,hA(xi)〉|xi∈X,i=1,2,…,n}.
(1)
其中,hA(xi):X→D[0,1]表示元素xi∈X属于集合A的所有可能区间隶属度组成的集合,称hA(xi)为一个区间犹豫模糊元(IVHFE),即
hA(xi)={γ|γ∈hA(xi)},
(2)
这里γ=[γL,γU]是一个区间数,γL=infγ和γU=supγ分别表示γ的下界和上界.
IVHFE是IVHFS的基本单元,它可以看成是IVHFS的一个特例.IVHFE和IVHFS之间的关系类似于区间值模糊数和区间值模糊集之间的关系.
定义2[12]假如a=[aL,aU],a=[aL,aU]为2个给定的区间数,la=aU-aL,lb=bU-bL,则a≥b的可能度为
(3)
(3)式可以用于比较2区间数的大小.
定义3对于任意的2个犹豫模糊元h1、h2,它们之间的的距离公式[19]如下:
(4)
(5)

2 广义区间犹豫模糊元的距离公式
假设有2个区间犹豫模糊元h1、h2,l=max{lh1,lh2},lh1、lh2分别表示区间犹豫模糊元h1、h2的区间数的个数.由于区间犹豫模糊元h1、h2中区间数的个数不总是相同的.因此,为了便于度量它们之间的距离可以运用添加原则,对区间数较少的区间犹豫模糊元添加或最大或最小的区间数,直到2个区间犹豫模糊元达到相同的区间数个数.有如下2种添加原则:一是乐观者原则,二是悲观者原则.乐观者原则即添加最大值直到lh1与lh2相等,悲观者原则为添加最小值直到lh1与lh2相等,则区间犹豫模糊元h1、h2的广义区间犹豫模糊元距离公式为
(6)
其中,λ>0,h1,σ(q)、h2,σ(q)分别表示区间犹豫模糊元h1、h2第q个最大值;区间数的大小按(3)式比较.
显然该定义满足距离测度的3个条件:
1) 0≤d(h1,h2)≤1,当且仅当h1=h2时,d(h1,h2)=0;
2)d(h1,h2)=d(h2,h1);
3) 设h3为任意的区间犹豫模糊元,则d(h1,h2)≤d(h1,h3)+d(h3,h2).
特别地,当λ=1时,d被称为区间犹豫模糊元海明距离;当λ=2时,d被称为区间犹豫模糊元欧氏距离.
3 区间犹豫模糊TOPSIS的多属性群决策方法
对于一个多属性群决策(MAGDM)问题,假如有n个备选方案可供选择,A={A1,A2,…,An};每一备选方案需要考虑m个属性,X={x1,x2,…,xm},则区间犹豫模糊决策矩阵H=(hij)n×m可以表示如下:
(7)
这里hij表示方案Ai在属性xj下属性评价值,hij以区间犹豫模糊元的形式给出.
考虑决策过程中,属性类别有2类:
1) 利益型属性,值越大越好;
2) 耗费型属性,值越小越好.需要将耗费型属性的值转化为利益型的值,即按(8)式原则将区间犹豫模糊决策矩阵H=(hij)n×m正则化为矩阵R=(rij)n×m,
(8)

3.1权重在多属性群决策过程中,每一属性具有不同的重要程度,因而,获得属性的权重向量至关重要.本文针对各决策者主观给出属性评价值的前提下,根据各属性评价值的最大化离差度寻求更加符合决策者心理的属性权重向量.最大化离差度确定权重的思想为:当某个属性在所有的备选方案之间具有越大的离差度时,赋予该属性较大的权重;当某个属性在所有的备选方案之间具有越小的离差度时,赋予该属性较小的权重.
对于属性xj∈X,方案Ai与所有备选方案之间的离差度计算如下:
i=1,2,…,n,j=1,2,…,m.
(9)
其中
d(rij,rkj)=
是区间犹豫模糊元rij与rkj之间的广义区间犹豫模糊元距离.令
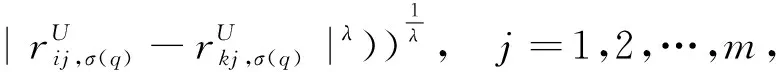
其中dj(w)表示属性xj∈X的所有备选方案与其他方案偏差度.
本文通过最大化离差度求解权重向量,建立非线性规划模型,模型如下:
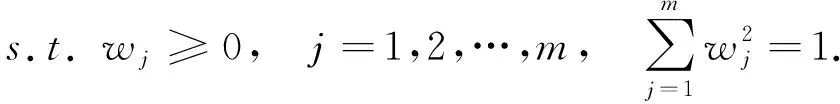
为了求解上述模型,令
(12)
(12)式表示上述优化模型的拉格朗日函数,其中ξ是一个实数,表示拉格朗日乘数变量.则f关于wj与ξ的偏导数分别为:
(13)
(14)
根据(13)和(14)式可以得到

(15)
令

(16)
所以
(17)
归一化权重向量
(18)
3.2利用IVHF-TOPSIS法确定贴近度通过最大化离差度法获取了各个属性的权重,在属性评价信息给定的情况下,需要寻求一种方法来综合评判每一方案的整体性能,然后对各个方案进行排序,从中选取最优方案.当属性评价值为区间犹豫元,如果采用复杂的聚合算子进行聚合,将造成决策信息的大量丢失,使得最终结果的可信程度降低.为了克服上述缺陷,本文扩展TOPSIS法,将区间犹豫模糊集和TOPSIS法想结合,提出区间犹豫模糊TOPSIS(IVHF-TOPSIS)法,用于解决属性评价值为区间犹豫模糊元情况下的多属性群决策问题.TOPSIS法的基本思想是在一组备选的方案中,选择一个离负理想解最远且离正理想解最近的方案.
因此,在区间犹豫模糊环境下,需要重新定义区间犹豫模糊正理想解A+、区间犹豫模糊负理想解A-,定义式如下所示:
j=1,2,…m;i=1,2,…,n〉}=
(19)
j=1,2,…m;i=1,2,…,n〉}=
(20)
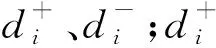
(21)
(22)
则方案Ai的相对贴近度系数为
(23)
不难发现
0≤c(Ai)≤1,i=1,2,…,n.
当一个方案离区间犹豫模糊负理想解越远且离区间犹豫模糊正理想解越近时,c(Ai)的值就越趋近于1,该方案也越好.因此,可以根据c(Ai)值的大小,对备选方案进行排序并选出最优方案.
3.3算法步骤在属性权重完全未知以及属性评价值为区间犹豫模糊元的条件下,本文给出基于区间犹豫模糊TOPSIS法的多属性群决策的决策步骤:
Step 1:对于一个多属性群决策(MAGDM)问题,决策矩阵H=(hij)n×m是由决策者以区间犹豫模糊元形式给出的.然后,根据(8)式将决策矩阵H=(hij)n×m正则化为矩阵R=(rij)n×m.
Step 2:在权重信息完全未知的条件下,运用(15)~(18)式计算属性权重向量w′.
Step 3:利用(19)和(20)式分别得到区间犹豫模糊正理想解A+,区间犹豫模糊负理想解A-.

Step 5:用(23)式计算得到每个方案Ai的相对贴近度系数c(Ai);
Step 6:根据每个方案Ai的相对贴近度系数c(Ai)的大小,对所有方案进行排序并选出最优方案.
4 实例分析
某网络零售企业为了提高其服务效率及质量,决定在某地区新建一个大型仓库,有3个备选地点A1、A2、A3可供选择.在仓库的选址过程中,需要综合考虑3个主要属性:城市的发展水平(x1)、销售目标市场及客户分布(x2)、交通条件(x3),它们都为利益型属性,如图1所示.邀请业内专家对3个备选地点的各个属性进行评价打分,属性评价值用区间犹豫模糊元来表示,得到对应的区间犹豫模糊决策矩阵H=(hij)3×3,如表1所示.
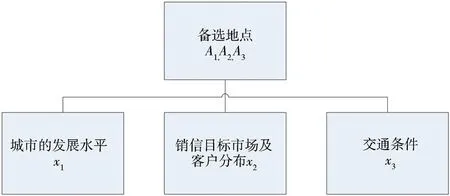
图 1 仓库选址考虑的3个因素
不难发现,表1中的各个区间犹豫模糊元的数量不同,为了方便计算各区间犹豫模糊元之间的距离,本文基于乐观者原则将表1中所有的区间犹豫模糊元的数量统一为3,扩充后的结果如表2所示.

表 1 区间犹豫模糊决策矩阵H=(hij)3×3

表 2 扩充后的区间犹豫模糊决策矩阵
由于所有属性都为利益型属性,不需要正则化.在此基础上,取λ=1,首先,运用(15)~(18)式分别确定属性x1、x2、x3权重,得到相应的权重向量w′=(0.3658,0.2927,0.3415).
然后,运用(19)及(20)式得到区间犹豫模糊正理想解A+和区间犹豫模糊负理想解A-:
A+={〈x1,{[0.7,0.8],[0.5,0.7],[0.3,0.4]}〉,
〈x2,{[0.4,0.7],[0.4,0.7],[0.4,0.7]}〉,
〈x3,{[0.7,0.8],[0.6,0.7],[0.6,0.7]}〉},
A-={〈x1,{[0.3,0.4],[0.3,0.4],[0.2,0.3]}〉,
〈x2,{[0.3,0.6],[0.3,0.6],[0.3,0.6]}〉,
〈x3,{[0.5,0.6],[0.5,0.6],[0.2,0.3]}〉}.

表 3 分离测度和贴近度系数
因为c(A1)>c(A3)>c(A2),所以最优的仓库选址为备选地址A1.
5 结论
本文将区间犹豫模糊元与TOPSIS法想结合,提出区间犹豫模糊TOPSIS法,并考虑了在权重信息完全未知的情况下,采用最大化离差度方法确定属性权重,选用本文提出的区间犹豫模糊TOPSIS法解决属性权重完全未知条件下的区间犹豫模糊群决策问题,从而进行方案排序优选.与已有多属性群决策方法相比,本文运用区间犹模糊元表示决策信息,一方面,由于区间犹模糊元在刻画客观世界的模糊性本质上更为准确,且更贴近实际生活;另一方面,本文是根据备选方案与正负理想解的贴近程度而进行的排序,相对于基于聚合算子的区间犹模糊多属性群决策方法,可以有效减少决策信息的损失.最后,将本文所提方法用于解决某网络企业的仓库选址问题,检验了本文方法的有效性.本文所提的区间犹豫模糊TOPSIS法也可以运用到其他领域排序优选类问题.

