S-格上的同余关系

齐彩霞, 阳 城, 郭兰坤*, 刘 丽,

(1. 湖南师范大学 数学与统计学院, 湖南 长沙 410006; 2. 湖南大学 数学与计量经济学院, 湖南 长沙 410012)

格是一类兼有序和代数的重要结构,最早由德国数学家Dedekind和Schröder分别从数论和逻辑代数2个角度提出,后来在美国数学家Birkhoff和挪威数学家Ore等的共同努力下,发展成为一门独立的数学学科.随着格论的发展,格与其它数学分支的联系及应用越来越紧密.例如著名的Stone对偶理论告诉我们,特殊的格结构与特殊的拓扑空间是对偶存在的[1];在Domain理论中,特殊的Domain结构可以借助一些内蕴拓扑,如Scott拓扑和Lawson拓扑,得到等价刻画[2];在形式概念分析理论中,一些特殊的格结构[3-4],如代数格,与特殊的关系结构之间存在范畴等价的关系[5].

同余关系是一类特殊的等价关系,有着非常广泛的应用,例如任意分配的双代数格序同构于同余格[6].另外,在抽象代数及数论当中同余关系的应用更加广泛[7].在一般格中,格上同余有许多良好的性质[8-10]，例如同余格在包含序下是分配的完备格.本文借鉴S-偏序集[11-15]的相关结果,在格上引入幺半群结构,提出S-格.注意到S-格可以看作格的一种推广方式,本文的主要目的是将格上的同余理论推广到S-格上.

1 幺半群与格上同余

定义1.1[16]设S是1个集合,·是S上的1个二元运算.若满足:

1)S是1个半群,即·运算是封闭和可结合的;

2) 存在e∈S,使得e·s=s且s·e=s对任意的s∈S都成立,则称(S,·)为1个幺半群.

为了方便,对任意s,t∈S,经常将s·t简记为st.

设(A,≤)是1个偏序集,若A的任意2个元的上下确界都存在,则称(A,≤)是1个格.此时,对任意a,a′∈A,用a∨a′(分别地,a∧a′)表示a和a′的上确界(分别地，a和a′的下确界).设(A,≤A)和(A′,≤A′)是2个格,f:A→A′是1个映射.若对任意的a1,a2∈A,f(a1∨a2)=f(a1)∨f(a2)且f(a1∧a2)=f(a1)∧f(a2),则称f为1个格同态.涉及到多个偏序集时,在不产生混淆的前提下,经常省略≤A中的底标A.

设(A,≤)是1个格,θ⊆A×A是A上的1个等价关系,若θ满足:对任意的a,b,c∈A,(a,b)∈θ可推得(a∨c,b∨c)∈θ且(a∧c,b∧c)∈θ,则称θ为(A,≤)上的1个格同余.为了论述方便,经常将(a,b)∈θ简记为aθb.

2 S-格同余与伪同余

定义2.1设(S,·)是1个幺半群,(A，≤)是1个格.若存在1个映射λ:A×S→A满足:

1) 对任意a∈A,λ(a,e)=a;

2) 对任意的a∈A以及s,t∈S,λ(a,st)=λ(λ(as),t),

下文称A(省略λ)是1个S-格,而且,为了表述上的方便，将λ(a,s)简记为as.对于a∈A以及s,t∈S，读者可以通过上下文区别as与st.

定义2.2设A是1个S-格,ρ是对应的格(A,≤)上的1个格同余.如果ρ和S作用是兼容的,即对于任意a,b∈A以及s∈S,(a,b)∈ρ可推出(as,bs)∈ρ,则称ρ是A上的1个S-格同余.

定义2.3设A和B是2个S-格,f:A→B是1个映射.若f是1个格同态,且f保S作用,即对任意的a∈A,f(as)=f(a)s,则称f是1个S-格同态.

定义2.4设A是1个S-格,σ是集合A上的1个二元关系.如果满足：

1) ≤⊆σ,

2)σ∘σ⊆σ,

3)σ和S作用是兼容的,

4)σ和A上的“∨”、“∧”运算兼容，

则称σ为S-格A上的1个伪同余关系.

性质2.1设ρ是S-格A上的1个S-格同余,则A/ρ也是1个S-格,称之为ρ诱导的S-商格,其中，A/ρ上的S作用为

[x]ρs:=[xs]ρ,

定理2.1设A是1个S-格,σ⊆A×A.如果σ是A上的1个伪同余,则有ρ=σ∩σ-1是A上的1个S-格同余,且ρ诱导的S-商格上的偏序(记为≤ρ)可完全由σ按如下方式决定:

≤ρ={([a]ρ,[a′]ρ)|(a,a′)∈σ}.

证明不难验证ρ是A上的1个等价关系.

设a,a′,b∈A且(a,a′)∈ρ,则有(a,a′)∈σ且(a′,a)∈σ.因为σ和A上的“∨”、“∧”运算兼容,所以,(a∧b,a′∧b)∈σ且(a′∧b,a∧b)∈σ.于是,(a∨b,a′∨b)∈ρ且(a∧b,a′∧b)∈ρ,因此,ρ是A上的1个格同余关系.另一方面,设(a,a′)∈ρ.由ρ的构造得(a,a′)∈σ且(a′,a)∈σ.因为σ和S-作用兼容,所以,对任意的s∈S,有(as,a′s)∈σ且(a′s,as)∈σ,即(as,a′s)∈ρ,于是ρ是A上的1个S-格同余.

定理2.2设A是1个S-格,σ⊆A×A,则σ是A上的1个伪同余,当且仅当存在S-格C和S-格同态φ:A→C使得

⟸ 按定义2.4的条件逐条验证即可.

定理2.3设A是1个S-格,ρ是格(A,≤)上的1个格同余,则以下命题等价:1)ρ是1个S-格同余;2) 存在A上的1个伪同余σ,使得ρ=σ∩σ-1;3) 存在S-格C和S-格同态φ:A→C,使得ρ=kerφ.

3 S-格上的同态定理

定理3.1设A和C是S-格,φ:A→C是1个S-格同态.

图 1

对任意的a∈A以及s∈S,有f([a]ρs)=f([as]ρ)=φ(as)=φ(a)s=f([a]ρ)s,说明f是保S-作用的,是1个S-格同态,而等式φ=f∘ρ#是很容易验证的.另外,设g是1个从A/ρ到C的S-格同态,且满足g∘ρ#=φ,则对任意的a∈A,g([a]ρ)=g∘ρ#(a)=φ(a)=f∘ρ#(a)=f([a]ρ),因此,f=g,证明了f的唯一性.

推论3.1设A和C是S-格,φ:A→C是1个S-格同态.则有ran(φ)={φ(a)|a∈A}继承S-格C上的偏序结构和S-作用,仍然是1个S-格,而且,在S-格同态的意义下,A/kerφ与ran(φ)是同构的.

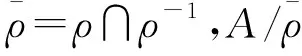
4 S-分配格上的S-格同余

定理4.1定义A上的二元关系θ如下:对任意a,a′∈A,有

则θ是A上包含α的最小S-格同余.

证明不难验证θ是A上的S-格同余.下证θ是A上包含α最小的S-格同余.

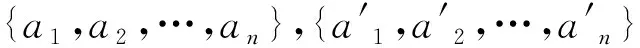
由于α⊆η,因此

于是,[a′]η≤[a]η且[a]η≤[a′]η,由此可得[a]η=[a′]η,即aηa′,因此,θ⊆η.

定义4.2设A是S-分配格,H是A上的二元关系.定义A上的二元关系α(H):对任意a,a′∈A,aα(H)a′当且仅当a=a′或者

a=(x1s1∨b1)∧c1,(y1s1∨b1)∧c1=

(x2s2∨b2)∧c2,…,(ynsn∨bn)∧cn=a′,

其中,(xi,yi)∈H,bi,ci∈A,si∈S.

定义4.3设A是S-分配格,H是A上的二元关系.定义A上的二元关系ν(H)如下:对任意a,a′∈A,有

不难验证α(H)是自反的、可传递的和保S-作用的,且与A上的“∨”和“∧”兼容.由定理4.1可得ν(H)是A上的S-格同余.

定理4.2设A是S-分配格,H是A上的二元关系,则S-商格A/ν(H)是分配的,并且对任意的a,a′∈A,有

[a]ν(H)≤ν(H)[a′]ν(H)⟺a≤α(H)a′.

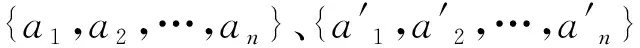
又由a∧a′≤a′,有

由于α(H)对A上的“∨”、“∧”运算兼容,所以

[a]ν(H)∧[a′]ν(H)=[a]ν(H),

意味着

[a]ν(H)≤ν(H)[a′]ν(H).

对任意的a,b,c∈A,

([a]ν(H)∧[b]ν(H))∨[c]ν(H)=

[a∧b]ν(H)∨[c]ν(H)=

[(a∧b)∨c]ν(H)=

[(a∨c)∧(b∨c)]ν(H)=

([a]ν(H)∨[c]ν(H))∧([b]ν(H)∨[c]ν(H)),

因此,A/ν(H)也是1个S-分配格.

定理4.3设A是S-分配格,H是A上的二元关系,则ν(H∪H-1)是A上包含H最小的S-格同余.

证明记θ(H)=ν(H∪H-1),设(a,a′)∈H,那么(a,a′)∈H∪H-1.由于a=(ae∨0)∧1,(a′e∨0)∧1=a′,因此

aα(H∪H-1)a′,a≤α(H∪H-1)a′.

设η是A上1个包含H的S-格同余.对任意a,a′∈A,aθ(H)a′,有

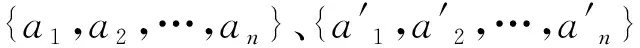
其中,aα(H∪H-1)a′当且仅当

a=(x1s1∨b1)∧c1,(y1s1∨b1)∧c1=

(x2s2∨b2)∧c2,…,(ynsn∨bn)∧cn=

a′,(xi,yi)∈H∪H-1,bi,ci∈A,si∈S.

由于H⊆η,并且η是A上S-格同余,因此H∪H-1⊆η,所以[a]η=[a′]η,即aηa′.于是θ(H)⊆η.由此可得θ(H)是A上包含H最小的S-格同余.

例4.1设集合S={e,a},S上的运算“·”如图2.

图 2

不难验证(S,·)是1个幺半群.

偏序集(A,≤)的序为图3.不难验证(A,≤)是1个分配格.定义映射λ:A×S→A有图4.

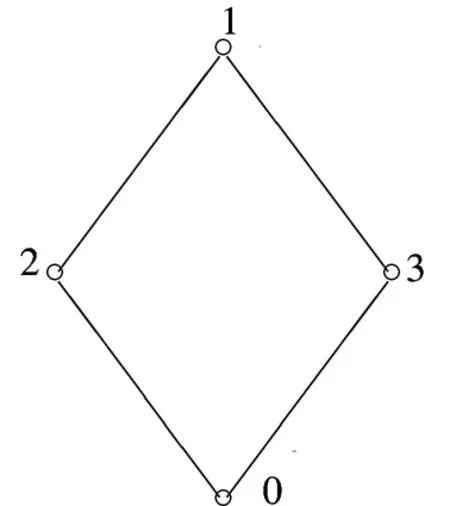
图 3

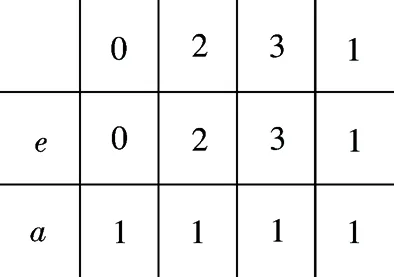
图 4

不难验证A是1个S-分配格.令H={(0,0)}⊆A×A,那么H∪H-1=H,α(H∪H-1)={(0,0),(2,2),(3,3),(1,1)},θ(H)={(0,0),(2,2),(3,3),(1,1)}.