基于ISO 13679的油管特殊螺纹接头密封可靠性分析*

杨 康，张建兵，谷天平，申维佳

(西安石油大学 机械工程学院，陕西 西安 710065)

0 引 言

随着我国油气田开发不断向深井、超深井等复杂井迈进，油气田对油套管，特别是螺纹接头的性能要求也越来越高，而确保油套管螺纹接头性能可靠对于油气田开发来说尤为关键[1]。

一般对于特殊螺纹性能的方法有三种：解析法、试验法、有限元分析法。在特殊螺纹研究的前期，多采用解析法，但由于特殊螺纹外形的复杂，解析法很难建立精确的数学模型。现行的试验法多以ISO13679：2002《石油天然气工业套管及油管螺纹连接试验程序》[2]为依据，采用全尺寸试验对套管螺纹接头进行评价。但是，试验法要求比较苛刻，国内具有评价试验资质的单位并不多[3]，这也间接地限制了特殊螺纹接头研究的发展。

随着计算机技术的不断发展，有限元方法逐渐成为众多研究人员优先考虑的方法。近年来，国外一些学者已将有限元分析技术应用于特殊螺纹的气密封性评价、疲劳设计、强度分析等方面[4-6]，国内的一些学者也已将计算机有限元分析用于油套管特殊螺纹的研究之中[7-10]。但是目前按照ISO 13679：2002对该类型油管特殊螺纹性能进行系统性的评价不多[11]。以Φ88.9 mm×6.45 mm规格为P110钢级的某特殊螺纹接头为分析对象，基于ISO13679:2002标准的试验程序和方法以及密封接触能理论，结合实物评价试验与有限元分析仿真分析，来综合评价特殊螺纹接头的密封性。

1 实物评价试验

1.1 油管特殊扣上卸扣性能评价

油管螺纹上卸扣实验结果数据见表1，上、卸扣前后照片如图1所示。

图1 试样上卸扣前后对比图

根据ISO 13679:2002、SY/T6128：2012标准及现场实际工况进行上、卸扣试验。该规格试样上扣扭矩为4 850 N·m。

实验表明，经过6上5卸后，油管特殊螺纹接头均未发生粘扣和密封面损伤现象。

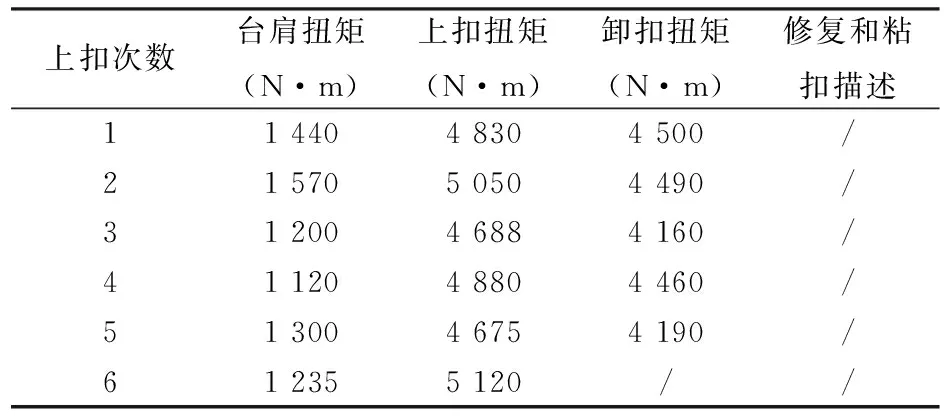
表1 试样上卸扣实验结果数据

1.2 高温环境复合载荷下特殊扣性能评价实验

图2为Φ88.9×6.45 mm规格P110S钢级的某特殊螺纹油管的名义强度三轴应力椭圆。结合应力图与实际情况选取载荷。

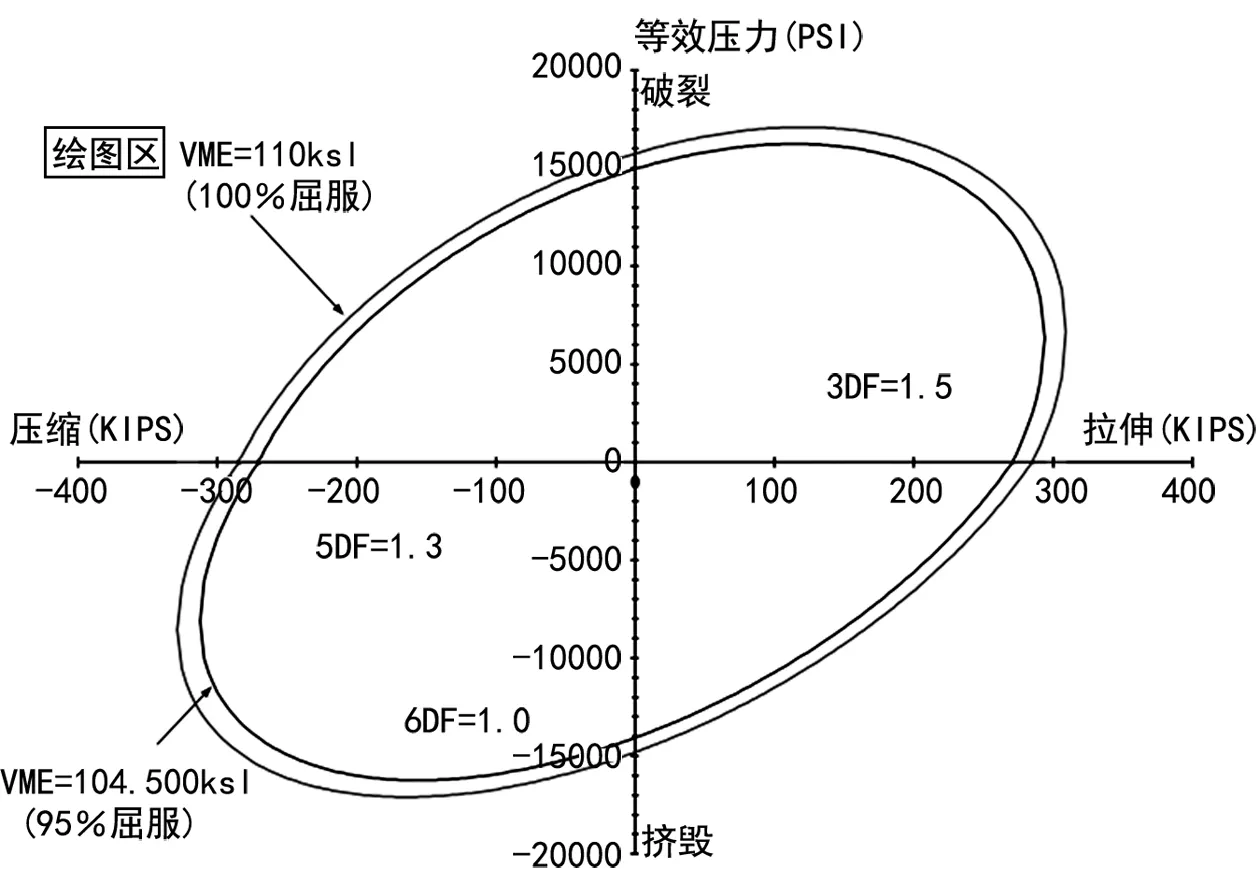
图2 Φ88.9×6.45 mm油管三轴应力椭圆

特殊螺纹接头复合加载实验的载荷条件及加载步骤见表2，其实验加载曲线图如图3。

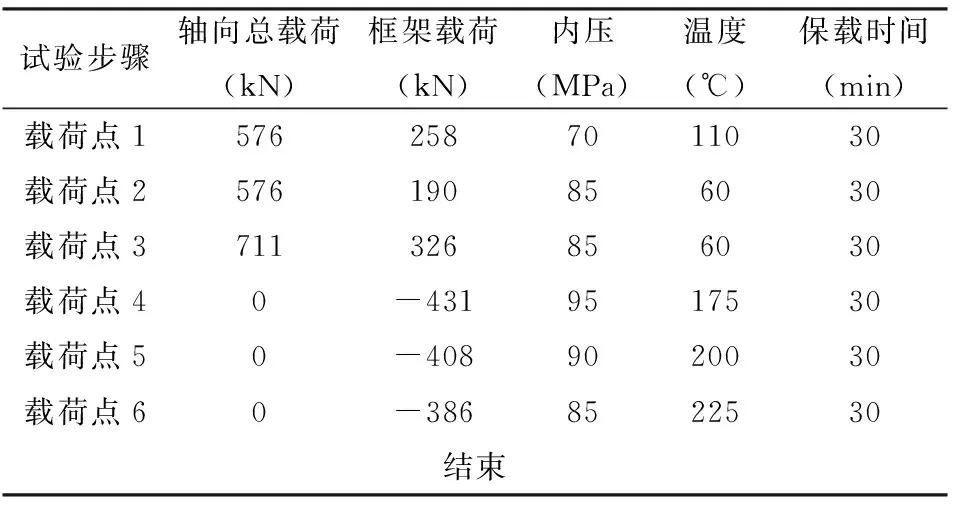
表2 试样拉伸/压缩条件下压力和温度复合 载荷实验加载步骤

通过实验观察，在整个复合加载实验过程中，试样未发生结构损坏，也未发生泄露，说明在给定载荷条件下，试样的密封性能良好。

图3 试样载荷包络线实验加载曲线图

2 特殊螺纹接头密封性能有限元分析

2.1 有限元方程

由油管接头的结构、材料及受力特点可知，在上扣和使用过程中，接头的变形往往会超出弹性变形的范围，因此必须同时考虑弹性变形和塑性变形。对于油管这种金属材料，在弹性区采用Hook定律，在塑性区采用Von Mises屈服准则以及Prandtl-Reuss塑性流动增量理论。对于油管接头在上扣、内、外压等过程中的受力分析，虽然发生了塑性变形但变形较小，即属于小变形弹塑性变形的范围，仍可以采用工程应力和工程应变作为应力度量和应变度量。这时弹性力学中的平衡方程和几何方程仍然成立，只是物理方程变为非线性的了，即为材料非线性问题。由于该方法忽略了微元体的变形，并认为位移与应变呈线性关系，只适合分析油管接头变形较小的受力过程。

如果塑性变形较大，如油管接头的挤毁失效等，则必须考虑由于大位移和大转动对单元形状及有限元结果的影响，平衡方程必须相对于变形过的几何位置写出，应力-应变曲线也必须真实应力-对数应变曲线。真实应力、对数应变与工程应力、工程应变之间的关系，可由以下转换公式求得：

σ=(1+ε0)σ0

(1)

ε=ln(1+ε0)

(2)

式中：σ，ε为真实应力、真实应变；σ0，ε0为工程应力、工程应变。

在Updata Lagrangian方法中，虚功方程可以表示为：

(3)

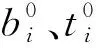
将应力与共轭应变带入上述虚功方程，即可得到单元的平衡方程式：

{K1+K2}δ=F-R

(4)

式中：K1、K2为材料刚度矩阵、几何刚度矩阵；F、R为内力、外力。

在非线性问题中，K1和K2已经不是常数矩阵，在它的各个元素中还包含节点的位移分量，所以由各个单元的平衡方程式集成的整个结构的有限元方程，是一个非线性代数方程组，一般用牛顿―拉斐逊方程或修正的牛顿―拉斐逊方程求解[12]。

2.2 密封判定条件

密封接触能机理认为，阻止气体通过金属对金属密封结构的流动阻力可由密封接触强度fs表征，它定义为密封接触应力在有效密封长度上的积分值[13]：

(5)

式中：fs为密封接触强度；N/mm；Les为有效密封接触强度，mm。

Murtagia[14]等通过物理试验和数值模拟方法研究了静态金属对金属密封面密封性能与密封接触应力剖面的经验函数关系，他们提出的评价金属对金属密封性能参数Wa定义为：

(6)

式中：Wa为金属对金属密封性能评价指数，mm·MPa1.4。

他们通过大量实验，提出金属对金属的临界密封指数为：

Wac=

(7)

式(7)的结论是基于室温条件下的，在更苛刻环境下(高温高压环境)，螺纹脂受高温影响，性能产生变化，因而选用无螺纹脂的试验参数进行计算。

同时，Murtagian等认为当Wa大于某个临界值Wac时，特殊螺纹接头的密封性能较好。而Xie[15]等人采用有限元模拟的方法，同时考虑高温高压气井油管实际密封失效经验和已有数据的回顾并结合ISO13679中规定的极限泄漏速度又提出了高温高压油套管特殊螺纹连接时Wac的计算公式为：

(8)

式中:Wac为临界密封指数，mm·MPa1.4；Pgas为管内压力，MPa；Patm为大气压力，MPa。

结合式(6)和式(8)，当Wa>Wac，可以认为该特殊螺纹接头的密封性良好。

2.3 有限元模型

建模及分析过程中，模型均采用接头名义尺寸建立。考虑到接箍及管体的轴向对称特性，且螺纹的螺旋升角非常小(小于1.0°)，可将接头简化为二维轴对称模型。其中，接箍沿轴向取其一半长度；为消除边界效应，管体不带螺纹的部分长度应大于管端至消失点距离的2倍以上。材料的弹塑性模型基于等向强化模型建立，且不考虑材料屈服点附近的应变率变化。其材料性能如表3。

表3 特殊螺纹接头力学性能

考虑到螺纹、密封面和台肩部位存在的过盈量以及接触分析的需要，在这些部位需要对模型网格进行细化，从而保证更准确和可靠的分析结果，其有限元网格模型见图4。上扣后的等效应力云图见图5。

图4 螺纹接头网格模型

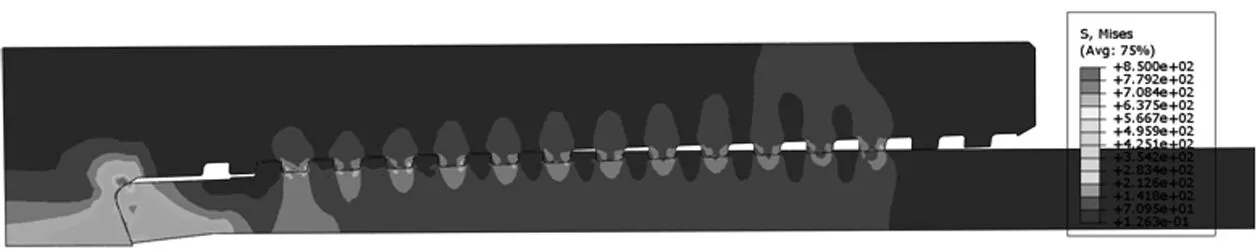
图5 上扣后的等效应力云图

如图5所示，主密封面与扭矩台肩处有较大的应力集中，其中最大等效应力(850 MPa)出现在主密封处，而扭矩台肩处应力较小。也说明了密封面承担了上扣扭矩产生的主要径向力，起到了密封作用。

2.4 仿真结果分析

在ISO13679标准中，包括A、B、C三个系列载荷，而A系列试验最为接近实际情况。因此，采用A系列载荷试验的仿真结果对该型特殊螺纹接头进行分析。特殊螺纹接头载荷点取值情况如表4所示。

计算得到的特殊螺纹接头在不同载荷下的密封接触强度，如表5、6所示。

按上表中对应的临界密封指数作为泄露标准(令Wa=Wac)，由式(6)计算基于密封面平均接触应力，在不同密封有效接触长度情况下的金属对金属密封结构的密封包络线，取压力不同的4组数据进行对比。

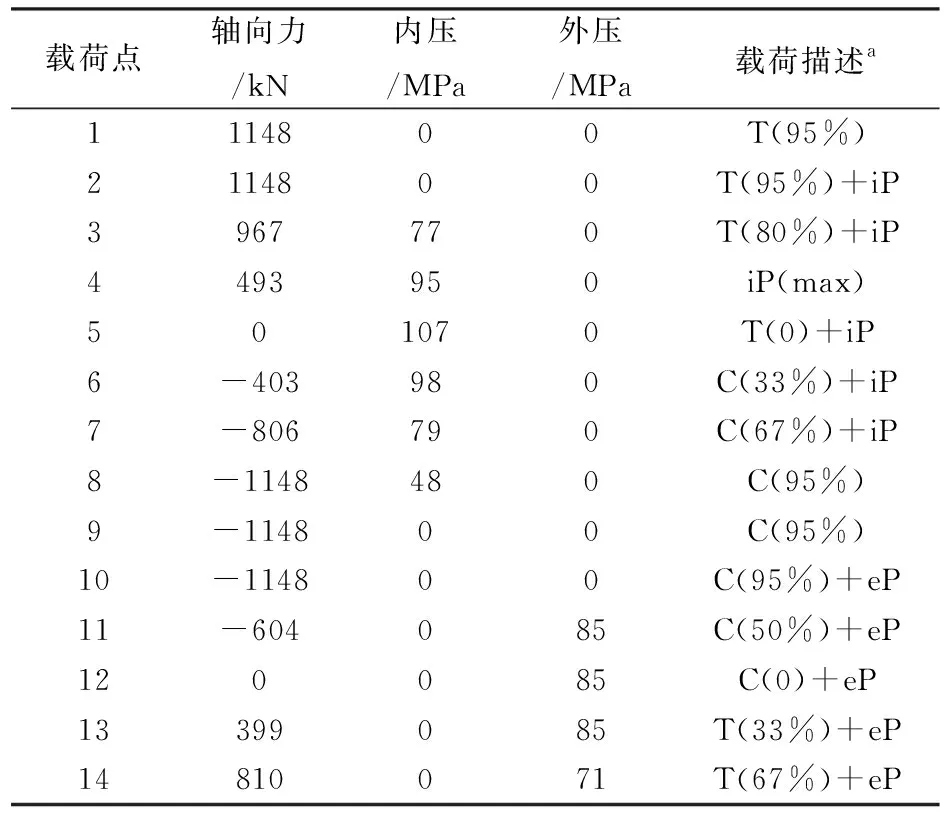
表4 某型特殊螺纹接头有限元计算载荷点取值

注：T：轴向拉力(拉伸屈服载荷的百分比)；C：轴向压缩(拉伸屈服载荷的百分比)；iP：内压；eP：外压。

表5 特殊螺纹接头在不同载荷下的密封接触强度

注：fs根据公式(2)～(5)计算获得。

如图6所示，当选取的参数组合(Led，Psa)位于密封包络线下方区域时，其密封指数已经小于临界值，特殊螺纹接头的密封性能将无法保证，密封结构发生泄漏。所以选取密封包络线上方的参数组合(Led，Psa)能够有效提高特殊螺纹接头密封性能。从图中可以得知，内压的大小也会影响Led和Psa的取值。特殊螺纹接头在受到较大内压时，其Psa和Les值大于其受到较小内压时的Psa和Les值。上述这些也为评价特殊螺纹接头的密封性能、密封结构的优化设计提供了重要依据[16]。同时，可依据密封评价条件，结合现场实际工况(井下需要密封的最大压力为120 MPa左右)对多种载荷工况条件下特殊螺纹接头的密封性能进行评价，如图7所示。

图6 基于密封接触能机理的金属对 金属气密封包络线

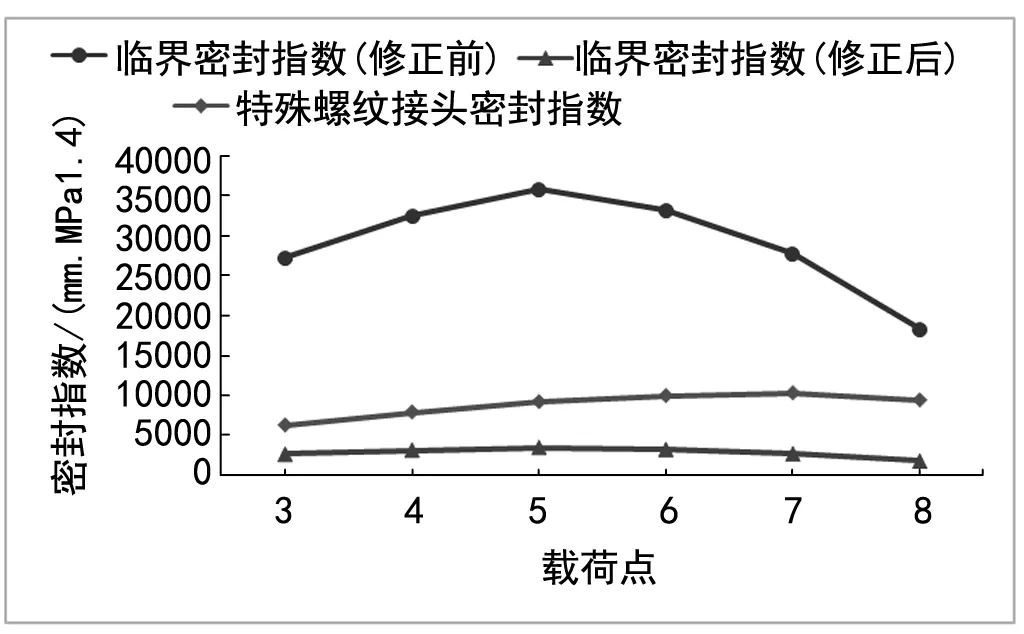
图7 多种载荷工况下特殊螺纹 密封指数评价图

图7是在对应载荷点的工况下，特殊螺纹接头临界密封指数的变化情况。而在不同工况下，特殊螺纹接头密封指数均处在两种临界条件之间，只满足其中一种密封要求。这可能是由于计算密封面临界密封指数(修正前)的公式，它没有考虑高温对接头性能的影响。采用式(8)给出的临界密封指数评价公式时，特殊螺纹接头满足密封性能要求。

分析对比上图数据，可知，增大轴向拉伸载荷或承受过高的内压会降低主密封结构密封性能[17]，但是适当增加轴向压缩载荷对提升主密封结构性能有益。

3 结 论

(1) 基于ISO13679：2002《套管和油管接头试验程序推荐做法》的拉伸/压缩条件下压力和温度复合载荷加载实验过程中，该试样完整性较好，未出现泄漏现象。说明按照现有的管柱结构设计以及实际工况，该型特殊螺纹接头扣型基本能满足给定条件下的力学载荷与密封性要求。

(2) 以某型特殊螺纹接头为分析对象，通过有限元方法进行仿真分析。基于密封接触能机理，得出密封包络线，定性地评价特殊螺纹接头的密封性能。与实物试验比对，说明了特殊螺纹接头具有良好的密封性，该种评价方法是评价特殊螺纹接头密封性能的一种有效方法，为之后的研究、设计、选用及优化提供依据。