波形钢腹板PC组合箱梁剪滞剪切效应的动力特性分析

马 驰， 刘世忠

(兰州交通大学土木工程学院，甘肃兰州 730070)

波形钢腹板PC组合箱梁是由波形钢腹板代替传统的混凝土腹板改进而成的一种新型组合梁桥。文献[1-3]对波形钢板、波形钢腹板Ⅰ型钢梁及波形钢腹板PC组合箱梁桥的抗剪强度、剪切屈曲开展研究。文献[4-5]研究波形钢腹板剪切变形对波形钢腹板组合梁受力行为的影响，提出把该结构在承受弯曲荷载作用时的变形形式分离成桁架和弯曲作用计算钢腹板剪切变形。文献[6]制作波形钢腹板混凝土试验箱梁，对试验箱梁的动力特性进行计算和分析。文献[7]导出分析波形钢腹板组合箱梁桥扭转振动的有效办法，证明设置横隔板可以提高结构的抗扭惯性矩，改善动力特性。文献[8]基于能量变分理论，得到计入剪力滞与剪切变形效应的波形钢腹板简支箱梁结构自振频率解析解。文献[9]考虑剪滞剪切效应的影响，运用能量变分法与Hamilton原理，推导获得该桥型自由弯曲振动的控制微分方程，以提高波形钢腹板组合梁桥的自振频率计算精度。文献[10-14]对薄壁箱梁剪力滞、剪切变形双重效应的自振特性进行分析研究。现阶段，很少有学者对波形钢腹板组合箱梁剪滞剪切双重效应的自振特性进行研究。本文利用能量变分原理，考虑剪滞剪切变形双重效应，在获得单元刚度矩阵和等效节点荷载矩阵的基础上，推导波形钢腹板组合箱梁的一致质量矩阵，使波形钢腹板组合箱梁矩阵位移法更加系统、完整，为计算波形钢腹板组合箱梁的剪滞剪切效应提供一种新的分析方法。

1 波形钢腹板组合箱梁的控制微分方程及单元刚度矩阵

图1所示的波形钢腹板组合箱梁在对称弯曲作用下，截面上梁的竖向挠度为W(x)，弯曲挠度引起的转角为φ(x)，其纵向位移U(x,y,z)满足

( 1 )

式中：x、y、z分别为桥梁纵向、横向、竖向坐标；b为箱梁净宽的一半；u(x)为最大纵向位移差函数。

图1 波形钢腹板箱梁横截面

根据文献[14]，波纹钢腹板的有效剪切模量计算公式为

( 2 )

式中：Es为钢材的弹性模量；νs为钢材的泊松比。其他结构参数如图2所示。

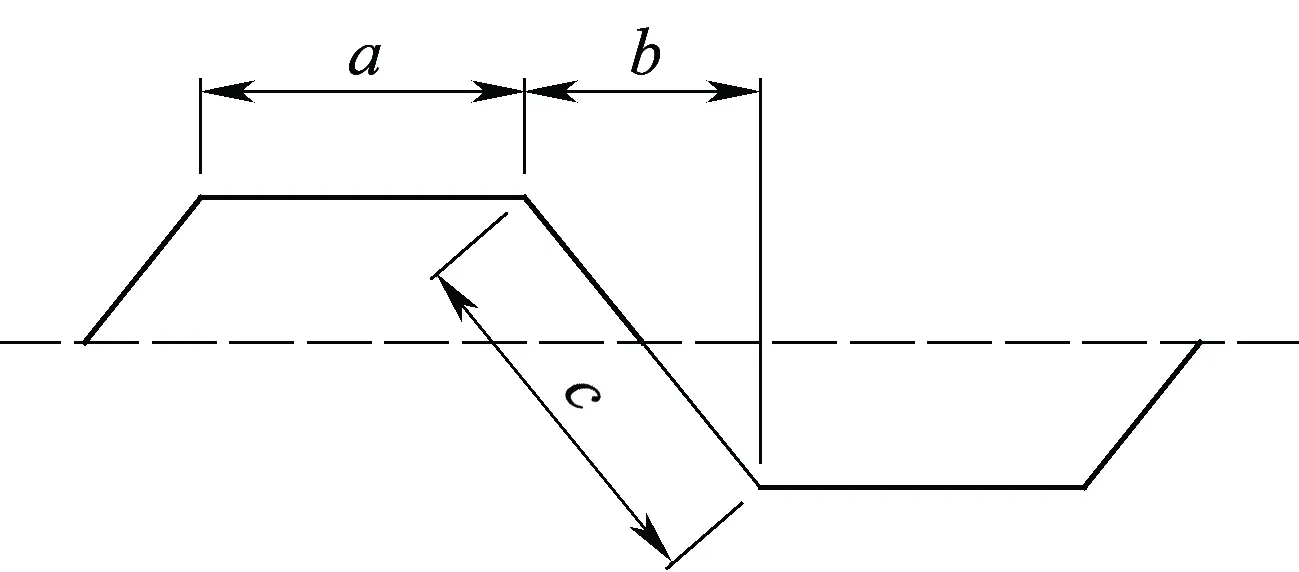
图2 波形钢腹板几何参数

波形钢腹板部分仅考虑剪切应变能，忽略其弯曲应变能，波形钢腹板剪应变γxz=W′(x)-φ(x)，W′(x)为竖向挠度W(x)一阶导数，全梁应变能为

( 3 )

式中：E为混凝土的弹性模量；ε为纵向应变；G为混凝土的剪切模量。

设z方向的、沿纵向分布的荷载为q=q(x)，l为梁长，M、Q为梁右端的弯矩和剪力，外力做功为

( 4 )

总势能为Π=V-Γ，由最小势能原理δΠ=0得到波形钢腹板组合箱梁的控制微分方程组及自然边界条件为

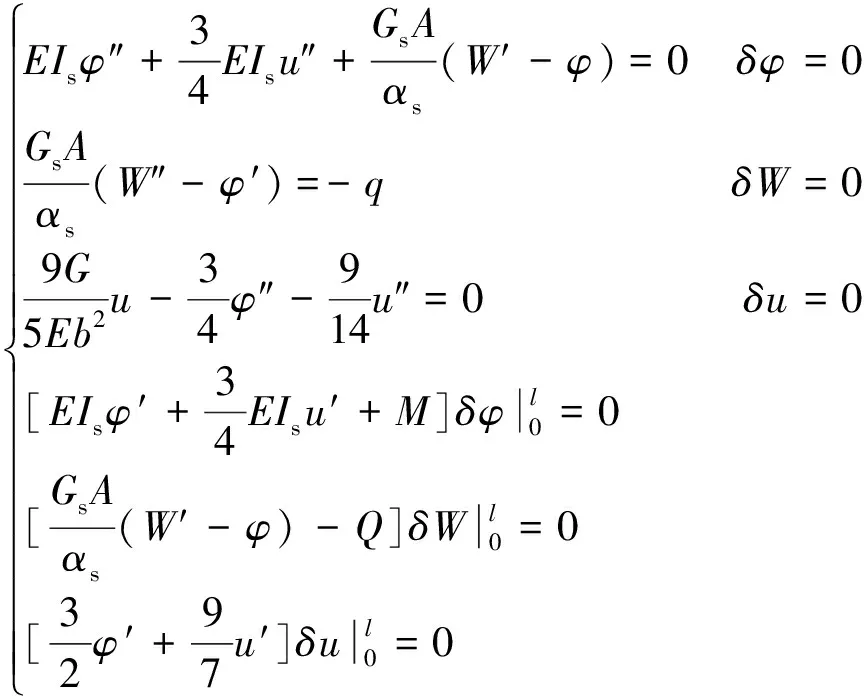
( 5 )

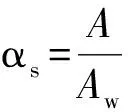
波形钢腹板组合箱梁在均布荷载作用下的初参数解为

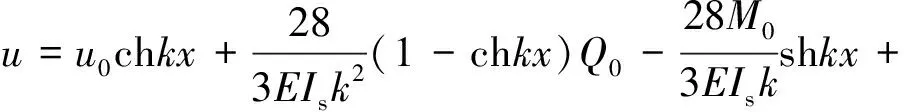
( 6 )

( 7 )

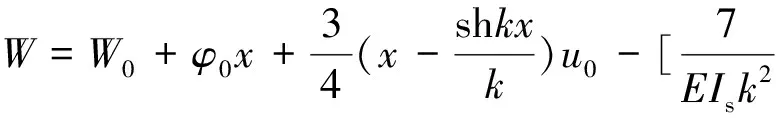
( 8 )

将x=l代入式( 6 )～式( 8 )，整理可得均布荷载作用下直线梁单元平衡方程为

( 9 )

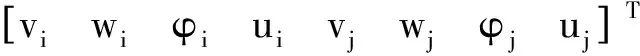
(10)

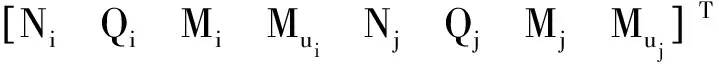
(11)

(12)

式中：i表示单元左端；j表示单元右端。

(13)

等效结点荷载列阵中的元素分别为

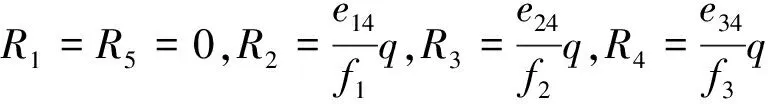
(14)

式(13)、式(14)中各符号的意义如下：

(15)

2 波形钢腹板组合箱梁的质量矩阵和运动方程

由虚功原理导出局部坐标系下波形钢腹板组合箱梁单元的质量矩阵为

(16)

式中：Ne为形函数矩阵，它是梁单元内部结点坐标的函数，与时间t无关。

令式( 6 )～式( 8 )中的q=0并写成矩阵形式

(17)

(Ki)3×6(δe)6×1=(Fi)3×1+(Ri)3×1

(18)

由式(18)可得

(19)

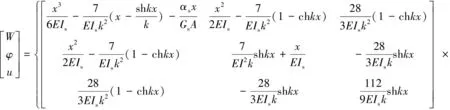
(20)

式(20)中δe的系数矩阵就是形函数矩阵Ne，将Ne代入式(16)即可导出考虑剪力滞、剪切变形效应的波形钢腹板组合箱梁单元质量矩阵，单元质量矩阵的形式为(Me)6×6，矩阵中各元素的表达式较复杂冗长，不再列出。

根据虚功原理可得局部坐标系下平面梁单元的运动方程

Meδe+Keδe=Fe

(21)

式中：Ke为局部坐标系下的单元刚度矩阵；Me为局部坐标系下的质量矩阵。

根据平面结构有限元理论组集系统坐标系下的单元刚度矩阵与一致质量矩阵，并列出各结点满足的平衡条件，即可得到整个结构的运动表达式

Mδ+Kδ=P

(22)

式中：δ为结点位移总矢量；P为已知的结点荷载总矢量；K和M分别为系统的总刚度矩阵和总一致质量矩阵。

3 动力特性分析

结构系统的重要动力性能是自振特性,即结构系统无阻尼自由振动的频率与相应振型，求解自振特性的过程即确定结构系统的振动频率与其相应振型的过程。

在式(22)中令P=0，得

Mδ+Kδ=0

(23)

式(23)为结构的无阻尼自由振动方程[15]，式(23)基本解的一般形式应为

δ(t)=φsin(ωt+β)

(24)

式中：φ为非零n元列向量，它的各分量之间无关；ω与β为待定常量。

式(24)的基本解表示的是以ω为圆频率的简谐振动，而φ则为与ω相应的振型，β为相位角。

将计算出的基本解代回式(23)，即可得到确定圆频率ω与相应振型φ的方程

Kφ=ω2Mφ

(25)

这是一个广义特征值问题，也称为振动特征值问题。

式(25)可改写为

(K-ω2M)φ=0

(26)

式(26)为关于φ的n个分量的线性代数齐次方程组，该方程组存在非零解φ的充要条件为

det[(K-ω2M)φ]=0

(27)

由式(27)可确定ω，称该式为频率方程。记

λ=ω2

并记

p(λ)=det(K-λM)

(28)

称p(λ)为振动特征值问题的特征多项式，而方程p(λ)=0的根称为特征根。

由频率方程式(27)解得n个ω，代入式(26)后，可得到非零解φ，即相应的振型。本文利用子空间迭代法编制求解广义特征值的Fortran语言程序BXBOX。

4 算例分析

4.1 算例1

按照本文单元刚度矩阵和一致质量矩阵建立运动方程,对文献[8]中的波形钢腹板组合箱梁进行计算。该试验箱梁跨度为9.745m，模型横截面尺寸参照文献[8]中的图3。箱梁混凝土的实测弹性模量为3.45×104MPa，泊松比为0.167，钢材弹性模量为1.95×105MPa，泊松比为0.3。本文把该试验梁分为40个单元进行计算，本文方法计算结果与文献[8]提供的一般梁理论、有限元及实测法所得的结果列于表1。其中一般梁理论为不考虑剪力滞及剪切变形效应的结果，本文方法为考虑剪力滞及剪切变形效应的结果。

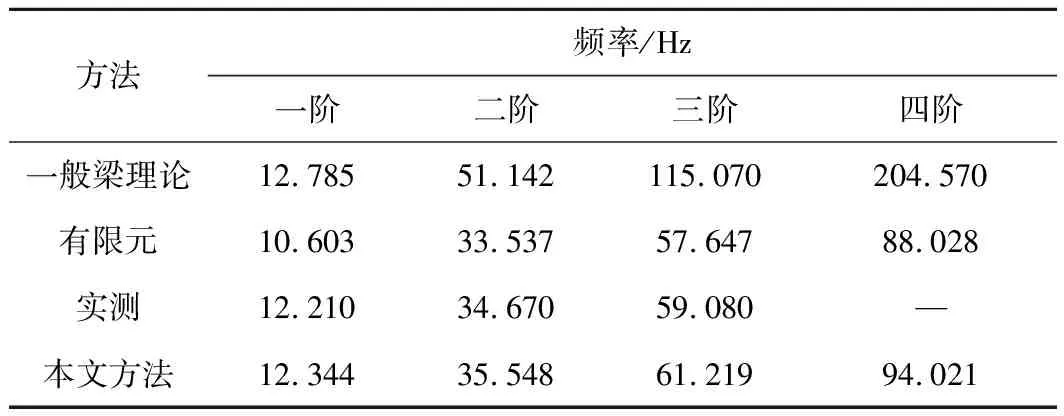
表1 波形钢腹板组合箱梁的自振特性

由表1可以看出，本文计算结果与有限元法和实测所得的结果吻合较好，验证了本文方法的正确性。本文方法计算结果相对一般梁理论计算结果精度大幅提高，随着阶次的升高一般梁理论误差也在增大，本文计算方法的计算量小，计算精度高，可用于考虑剪力滞及剪切变形效应自振特性的分析计算，且可得到与文献[8]同样的规律，考虑剪力滞及剪切变形效应后，波形钢腹板组合箱梁的自振频率有所降低，且降低程度随着阶次的升高迅速增大。

4.2 算例2

模型试验梁为简支箱梁，截面梁长为5 m，采用C50细石混凝土，实测抗压强度平均值为49.7 MPa，泊松比为0.2，弹性模量为34.5 GPa；波形钢腹板选择Q235，波纹板型号为H1600，厚度为2 mm，实测钢材弹性模量为206 GPa，泊松比为0.3；普通钢筋采用φ6钢筋，预应力筋采用1860级7φ5的钢铰线。试验梁横截面尺寸、纵向立面尺寸如图3、图4所示，波形钢腹板波形形状如图5所示。本文建立ANSYS实体模型[16]、考虑剪切变形的Midas梁单元模型和不考虑剪切变形的Midas梁单元模型，实体模型中箱梁顶板与底板采用solid45单元，波纹板采用薄壳单元shell63单元，且三者采用共节点方式连接，采用8节点的单元对实体模型进行网格划分， ANSYS有限元模型如图6所示，模型试验梁如图7所示。

图3 模型梁横截面设计尺寸(单位：mm)

图4 模型梁纵向立面尺寸(单位：mm)

图5 波形钢腹板波形形状平面图(单位：mm)

图6 试验梁有限元模型

图7 模型试验梁

对波形钢腹板简支梁和连续梁进行动力效应测试，获得其振动频率及相应的振型，采用东华DHDAS信号测试分析系统对室内模型试验梁进行动力特性测试，试验梁的模态试验采用瞬态激振法，采样频率为512 Hz。模型试验梁上布置DHDAS动态信号采集器，如图8所示，该设备可以采集竖向和横向的动态信号。为避免所关心频率的丢失，冲击荷载的位置根据结构的振型确定，应避免敲击点设置在结构前几阶模态振型的结点上。根据本试验模型振型的计算分析结果，进行敲击点和测点的布设，如图9所示。试验中保持激励位置不变，在激励位置发射脉冲信号，测量测点位置的加速度响应信号，通过分析程序进行模态拟合，得到试验梁的各阶振型。通常振动频率按由小到大的顺序排列，对应的振型也由简单变为复杂，如果计算实测没有发生漏根，结构的固有频率按次序排列与振型一一对应。

图8 DHDAS动态信号采集器

图9 采集器在上翼板的平面布置(单位：mm)

4.2.1 剪滞剪切效应对波形钢腹板简支箱梁自振特性的影响

采用本文编制的BXBOX程序分析波形钢腹板PC组合箱梁的振动行为，把简支梁分为4个单元5个节点进行计算,将实测值、本文计算值与数值模拟值的前四阶自振频率列于表2、表3。

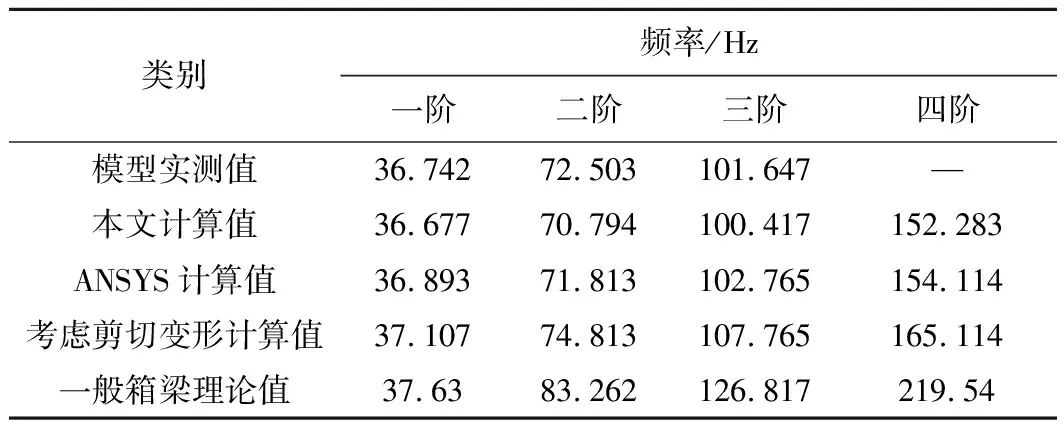
表2 剪滞剪切效应对简支梁自振特性的影响

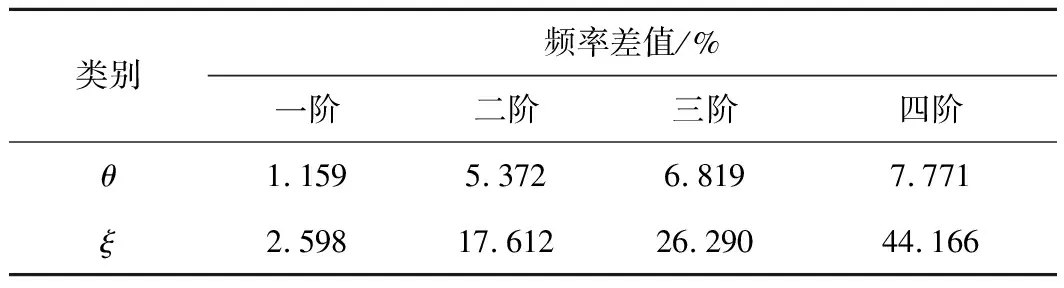
表3 不同方法间频率差值(简支梁)

考虑剪力滞和剪切变形双重效应的情况下，本文计算值与模型实测值、ANSYS数值计算值几乎完全吻合，验证了本文理论的正确性；其次采用Midas梁单元模型计算考虑剪切变形、不考虑剪切变形的工况以及不考虑剪力滞和剪切变形效应的工况(即一般的箱梁理论)。ANSYS实体模型的前四阶振型如图10～图13所示，一阶和二阶振型表现出梁竖向振动特性，三阶和四阶振型既表现出梁的竖向振动又有翼缘板沿梁轴线的振动特性。由表2、表3可知，剪切变形效应使梁内的自振频率降低，对高阶频率的影响更大，四阶时所得的结果频率差值达到了7.771%，一般箱梁理论值与本文计算值的频率差值在四阶时达到了44.166%，由此可知剪力滞效应对波形钢腹板组合箱梁的动力特性起主导作用。

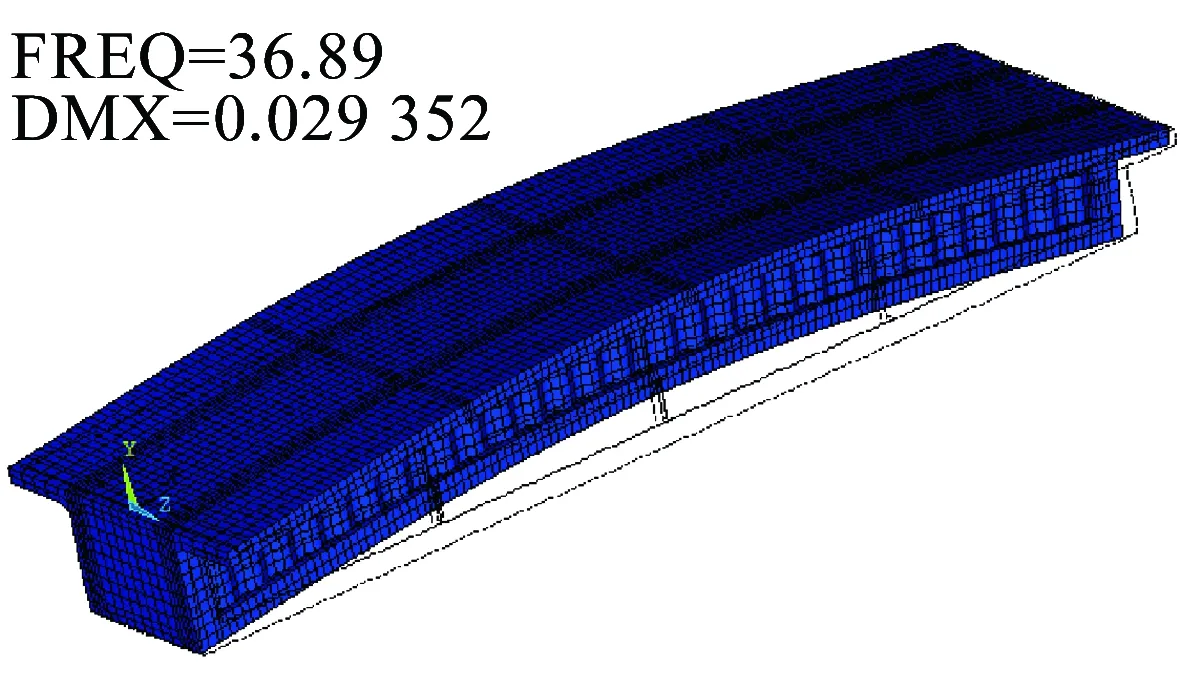
图10 简支梁一阶振型

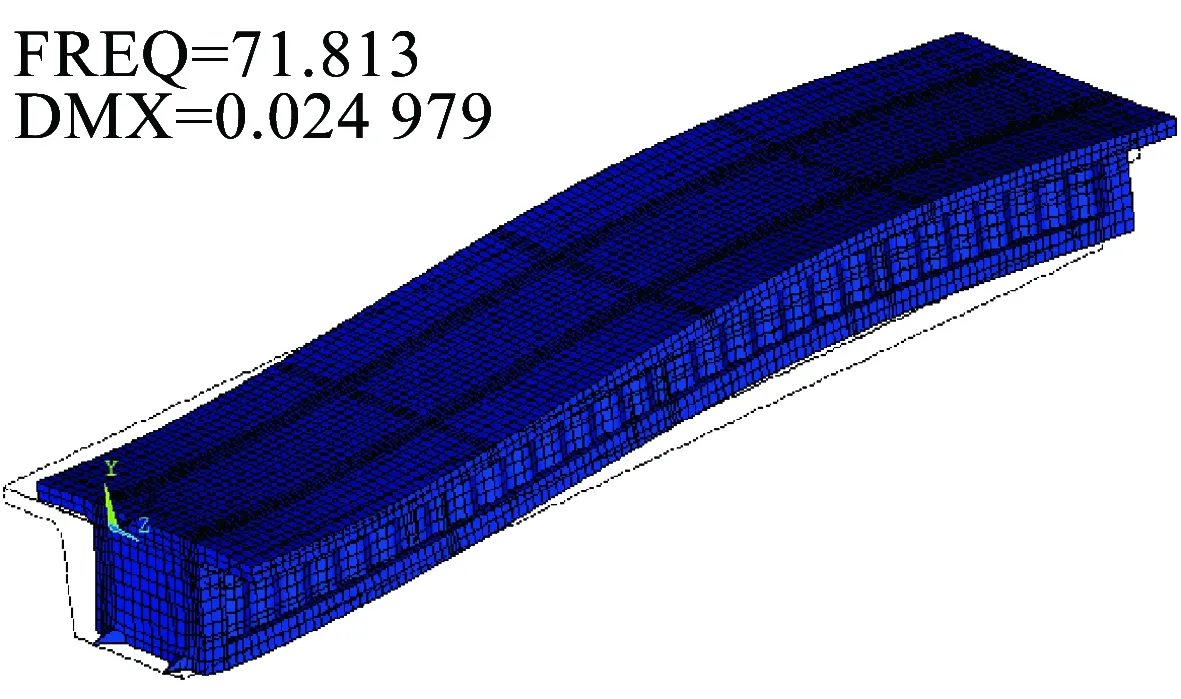
图11 简支梁二阶振型

图12 简支梁三阶振型

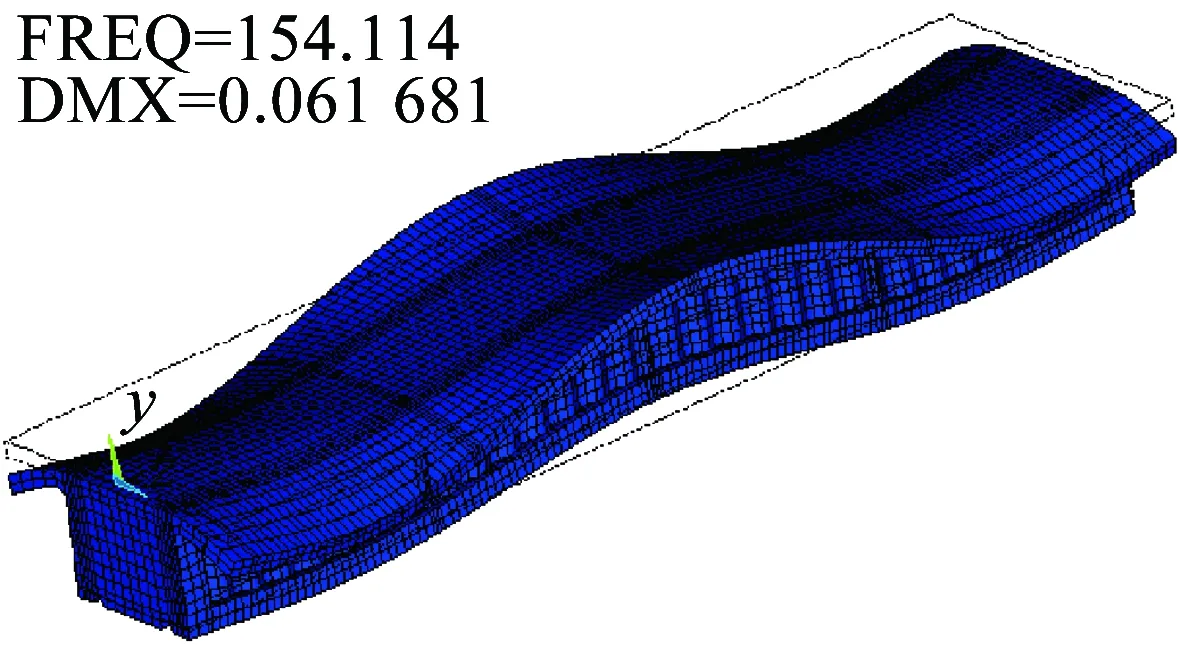
图13 简支梁四阶振型

4.2.2 剪滞剪切效应对波形钢腹板连续梁自振特性的影响

在算例2简支梁的基础上，在距离梁端2.5 m(即中横隔板位置)处的跨中截面上增加固定支座，使其变为两等跨连续梁(2.5 m+2.5 m)，边跨固定支座变换为活动支座，使简支梁变成如图14所示的连续梁，把全梁分为20个单元进行计算，并讨论考虑剪滞、剪切效应对两等跨连续梁振动特性的影响。将实测值、本文计算值与数值模拟值的前四阶自振频率列于表4、表5，连续梁表现出与表2、表3中简支梁相同的振动特性。

图14 连续梁的支座和单元节点

表4 剪滞剪切效应对连续梁自振特性的影响

表5 不同方法间频率差值(连续梁)

由表4和表5可知，本文计算值与模型试验值吻合良好，验证了本文理论的正确性。剪滞剪切变形效应使梁内的自振频率降低，对高阶频率的影响更大，四阶时所得的结果频率差值达到45.748%，规律与波形钢腹板简支箱梁相同。

5 结论

本文利用能量变分原理方法，考虑剪滞剪切变形双重效应，在获得单元刚度矩阵和等效节点荷载矩阵的基础上，推导出波形钢腹板PC组合箱梁的一致质量矩阵，使波形钢腹板PC组合箱梁矩阵位移法更加系统、完整，为波形钢腹板PC组合箱梁的剪滞剪切效应提供一种新的计算方法。与波形钢腹板PC组合箱梁的板壳或实体单元计算相比，计算量小、计算精度高，在工程实际中易于应用。算例表明：

(1)对于波形钢腹板简支箱梁和连续箱梁，本文计算值与模型试验值所得的自振特性值几乎完全吻合，验证了本文理论的正确性和可靠性。

(2)考虑了剪力滞与剪切变形双重效应的影响后，波形钢腹板PC组合箱梁结构的自振频率与Midas梁单元模型的模拟数值相比有所减小。这是因为剪力滞与剪切变形双重效应的影响使混凝土翼板与钢腹板的有效刚度降低，进而减小了组合结构的自振频率，对高阶频率影响较大。

(3)对波形钢腹板PC组合箱梁进行动力特性分析时，考虑剪滞剪切效应使结构自振频率明显减小，在四阶时约减小45%，剪切效应对其频率的影响在7%左右，剪力滞效应对该箱梁的动力特性影响更大。因此，对波形钢腹板组合箱梁进行动力特性分析时应考虑剪力滞和剪切变形效应的影响。