考虑电离层对GEOSAR影响的改进CS成像算法

王卓群，李亚军，李雁斌，顾网平，李 芬

(上海无线电设备研究所，上海 201109)

0 引言

地球同步轨道合成孔径雷达(GEOSAR)具有重访周期短和抗打击能力强等优点，在军事和民用领域中具有广泛的应用前景和发展潜力[1-6]。GEOSAR信号传输过程中，不可避免受到电离层影响。对于低轨合成孔径雷达(low earth orbital synthetic aperture radar, LEOSAR)来说，因合成孔径时间较短可忽略电离层对成像质量的影响。然而，GEOSAR一般工作于L波段，由于合成孔径时间较长，一般在小时量级，电离层的时间变化特性将严重影响该雷达的成像聚焦性能。

目前，国内外学者在电离层对星载SAR聚焦性能影响的研究方面已取得了一定的成果[7-11]，但相关研究主要集中在电离层对低轨SAR成像质量的影响，而针对GEOSAR聚焦性能影响的研究较少。李亮等[7]建立了电离层对中高轨道SAR系统的信号影响模型，分析了电离层时间变化对中高轨SAR成像质量的影响。JEHLE等[8]研究了受电离层污染的GEOSAR的回波信号模型，分析了电离层对距离及方位分辨能力的影响。然而，由于GEOSAR的轨道位置较高，合成孔径时间较长，该雷达不再满足“停—走—停”的假设，故收发路径中大气层引起的斜距误差也不相同[9]。

因此，本文基于非“停—走—停”假设，针对电离层影响GEOSAR成像质量的问题，提出了改进chirp scaling (CS)成像算法。首先，根据射线跟踪法推导电离层引起的双程斜距误差模型，理论推导受电离层影响的回波信号；其次，基于回波信号模型提出改进的CS成像算法；最后，仿真验证算法的有效性，该算法可较好地解决电离层引起的目标位置偏移和分辨率下降的问题，获得聚焦的成像结果。

1 电离层影响的回波信号模型

GEOSAR所发射的电磁波信号经过外部空间、电离层、平流层、对流层，最终达到地表目标，其反射信号被该雷达接收。其中，电离层中的大气折射导致电磁波的非线性传输。因此，本节详细分析了电离层折射所引起的斜距误差。

电离层不同于其他介质的主要参数之一就是电离层中的折射指数。在电离层中忽略电子碰撞和地磁场的影响，对于L波段的GEOSAR，其电离层折射率可表示为

(1)

式中：Ne(t0+ta,h)为在时刻t0+ta时电离层中的电子密度；f为信号频率；h为传播路径上任意点的高度。

由于掠射角趋近于90°，则电离层折射率变化引起的斜距误差为

(2)

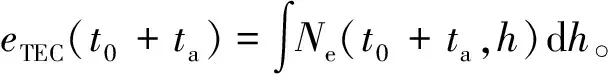
由于eTEC具有时间变化特性，现假设t0时刻的积分电子含量为eTEC0，则eTEC随慢时间ta变化为

eTEC(t0+ta)=

(3)

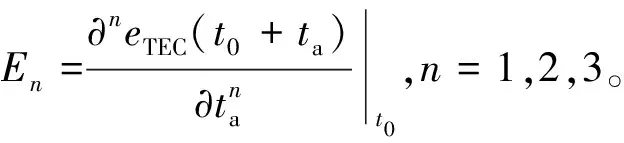
因此，电离层引起的接收天线与地表目标之间的斜距误差为

(4)

式中：τ为雷达发射电磁波到目标的电磁波传输时间。

根据式(2)和式(4)，推导得到电离层引起的双程斜距误差为

Rall-ion(t0+ta)=Rion(t0+ta)+Rion(t0+ta+τ)=

(5)

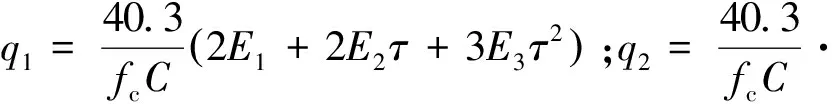
在距离频率-方位时间域，GEOSAR回波信号可表示为

Sion(fr,ta)=

(6)

式中：ρr(·)，ρa(·)分别为雷达线性调频信号的距离窗函数和方位窗函数；γ为雷达线性调频信号的调频率；C为波速；fc，fr分别为距离和方位频率；R(t0+ta)为理想情况下的斜距模型。

考虑到距离频率fr远小于载波频率fc，可忽略fr对方位脉冲响应的影响，则电离层污染的回波信号可进一步表示为

Sion(fr,ta)=AiS(fr,ta)Hir(fr)Hia(ta)

(7)

式中：

Ai=exp(-j2πq0)。

式(7)中：S(fr,ta)为GEOSAR的理想回波信号距离频率-方位时间域表达式；Hir(fr)和Hia(ta)分别为电离层对距离向和方位向脉冲响应函数的影响；Ai为电离层对回波信号幅度的影响。下面详细分析Hir(fr)和Hia(ta)对点目标聚焦性能的影响。

式(7)中(fc+fr)-1的泰勒级数展开式

Hir(fr)=

(8)

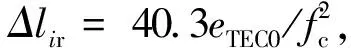
(9)

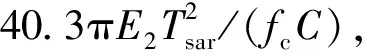
2 改进CS成像算法

GEOSAR的CS成像算法流程如图1所示，通过一系列成像处理步骤，最终获得清晰的点目标成像。

2.1 电离层影响处理步骤

步骤1：根据式(7)中电离层污染的GEOSAR回波信号Sion(fr,ta)，首先通过相位补偿消除电离层对距离向成像聚焦性能的影响，用双频时延差分估计法得到eTEC平均值，并用距离频率-方位时间域乘以Hir(fr)的共轭相位补偿函数conj(Hir(fr))，即

(10)

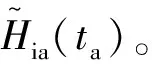
(11)

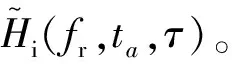
S′(fr,ta)=Sion2(fr,ta)·

(12)

基于上述步骤，处理后的信号中包含了理想回波信号S(fr,ta)和一小部分电离层影响残留信号Hi2(fr,ta)，有

Sion2(fr,ta)=S(fr,ta)Hi2(fr,ta)

(13)

通过方位向傅里叶变换，应用级数反演算法获得二维频谱，有

S(fr,fa)=ρr(fr)ρa(fa)exp(-j2πBa(fa))·

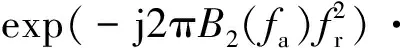
(14)

式中：Ba(fa)为方位调频相位；B1(fa)，B2(fa)，B3(fa)为距离与方位之间的耦合函数。

2.2 弯曲轨迹处理部分

步骤1：高阶相位补偿。由式(14)可知，GEOSAR的点目标二维频谱表达式存在高阶距离及方位耦合项[12]，这使得该雷达回波信号不同于参考CS的信号形式，因此，首先去除该高阶耦合项，即在二维频域乘以其高阶相位补偿函数，该补偿函数为

(15)

步骤2：CS相位函数处理。通过距离向逆傅里叶变换，获得回波信号的距离时间-方位频率域表达式。由于回波信号的多普勒调频率为K(fa)=1/(2B2(fa))，为构造CS相位函数，该信号可重新描述为

S1(tr,fa)=ρr(tr)ρa(fa)·

exp(jπK(fa)(tr-B1(fa))2)·

exp(-j2πBa(fa))Hi2(tr,fa)

(16)

对比CS信号形式，计算获得的CS因子，有

d(fa)=(CB1(fa)-2Rsc)/2Rsc

(17)

CS二次相位函数为

H2(tr,fa)=exp[jπK(fa)d(fa)·

(tr-B1(fa))2]

(18)

因此，CS处理后的回波信号为

S2(tr,fa)=

ρr(tr)ρa(fa)exp(-j2πBa(fa))Hi2(fr,fa)·

exp[jπK(fa)(1+d(fa))(tr-B1(fa))2]

(19)

步骤3：距离压缩处理与距离徙动校正。对式(18)的信号S2(tr,fa)进行距离压缩处理，即在二维频域乘以距离压缩函数，该函数为

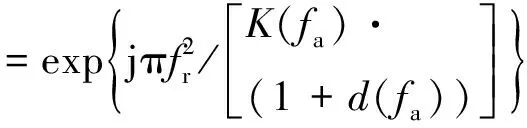
(20)

通过距离徙动校正将图像距离向聚焦于点目标斜距Rsm，其校正函数为

(21)

步骤4：方位压缩处理。在距离时间-方位频率域乘以方位压缩函数，该函数为

(22)

2.3 PGA算法处理

基于上述成像处理流程，回波信号仍存在残余电离层相位误差。引入传统的PGA技术[9]，使处理后成像结果聚焦于真实目标位置。

3 仿真分析

本节基于国际全球定位系统服务(IGS)提供的全球电离层网格数据，仿真分析电离层对L波段GEOSAR聚焦性能的影响，并验证改进CS成像算法的有效性。GEOSAR参数见表1。

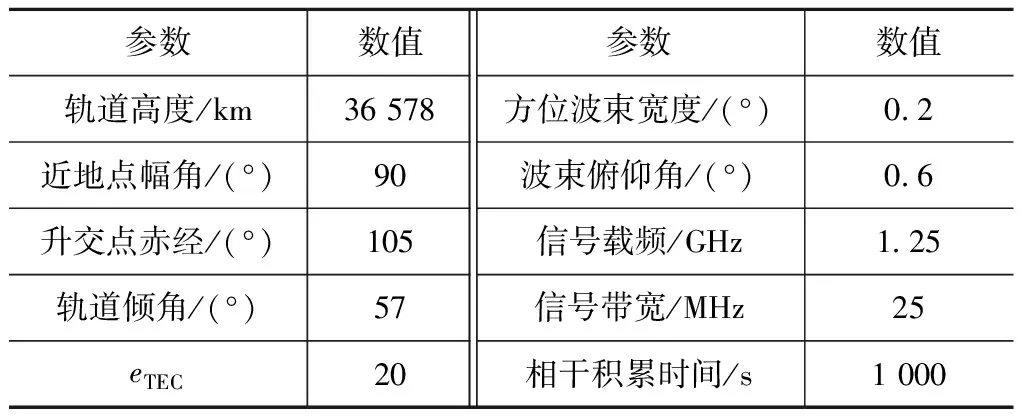
表1 GEOSAR参数Tab.1 GEOSAR parameters

根据IGS提供的2014年11月1日全球电离层网格图，以北京地区为例观测eTEC的日变化趋势，如图2所示。距离偏移量为4.7 m，距离相位误差为0.03 rad，方位偏移量为2.1 m，相位误差随相干积累时间的长度有关，在1 000 s的相干积累时间内的方位相位误差为4.7 rad。

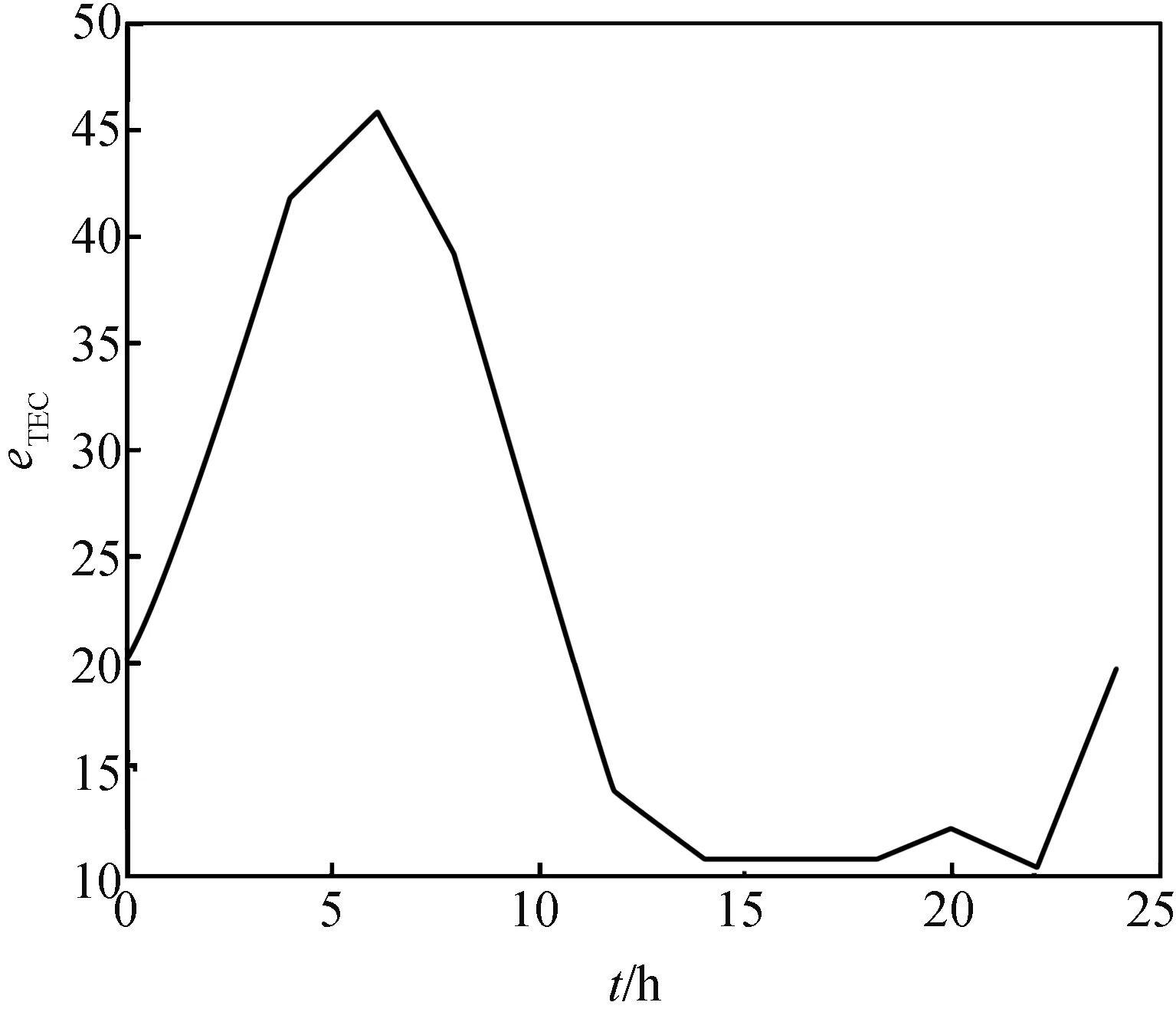
图2 北京某地区eTEC日变化趋势(2014年11月1日)Fig.2 Daily variant tendency of eTECin Beijing (November 1st, 2014)

研究当相干积累时间为1 000 s时，电离层对成像聚焦性能的影响及改进CS算法的成像效果，如图3所示。距离及方位分辨率理论值分别为6 m和3.15 m。由于受电离层影响，距离向偏离场景中心位移量为4.72 m，方位向偏离场景中心位移量为2.11 m。其成像质量如下：在距离向ΔIRW=6 m，ΔPSLR=-13.25 dB，ΔISLR=-10.14 dB；在方位向ΔIRW=5.89 m，ΔPSLR=-0.51 dB，ΔISLR=-2.92 dB。

用基于GEOSAR的改进CS成像算法，图像成像将聚焦于场景中心，其成像质量如下：在距离向ΔIRW=6 m，ΔPSLR=-13.25 dB，ΔISLR=-10.14 dB；在方位向ΔIRW=3.17 m，ΔPSLR=-13.14 dB，ΔISLR=-10.92 dB。对比二维分辨率理论值可知，用本文提出的改进CS成像算法可有效消除电离层对GEOSAR聚焦性能的影响，获得高精度成像结果。

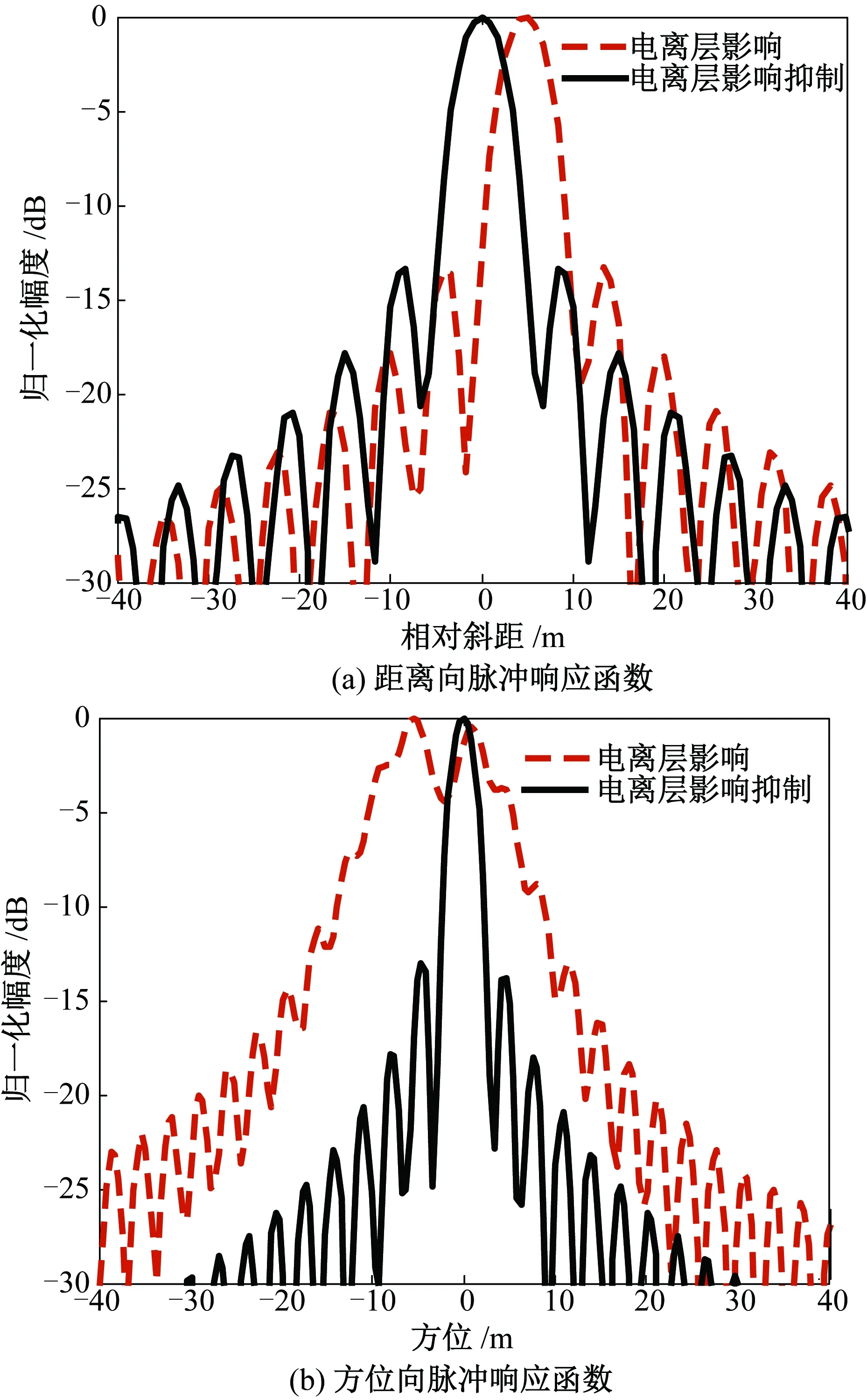
图3 电离层影响及其抑制处理后的成像结果Fig.3 Ionospheric effects and imaging results obtained by eliminating ionospheric influences

4 结论

本文针对电离层引起的成像散焦问题，提出了基于GEOSAR的改进CS成像算法。在非“停—走—停”假设下，考虑到电离层大气折射率引起的斜距误差，以及时延引起的双程传播路径不同，推导了电离层影响的斜距误差及回波信号模型，并基于此，提出了改进CS成像算法，主要包括电离层影响处理、弯曲轨迹处理及PGA自聚焦三部分。仿真结果表明：电离层导致了距离向偏移和方位模糊问题，改进CS算法则可有效处理该问题，获得清晰的成像结果。