基于直升机平台SAR的方位重影抑制方法

景国彬，王 辉，郑世超，孙光才，邢孟道

(1. 上海航天技术研究院 毫米波遥感技术重点实验室，上海 201109； 2. 上海航天技术研究院 毫米波遥感技术重点实验室，北京 100086； 3. 西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

0 引言

随着合成孔径雷达(SAR)技术的不断发展，高分辨率SAR在多种搭载平台得到了很好的应用[1-5]。直升机依靠灵活的机动性，可完成垂直起降，贴地飞行，且具有在任何地面条件下均可着陆的优势，这将使得SAR具有更广泛的应用前景[6-8]。地震发生后，通常会伴随恶劣天气，常规的光学遥感无法勘测地震灾情，而SAR具备全天时、全天候的对地观测能力，可实现灾情勘测[8]。因此，进行基于直升机平台的高分辨率SAR成像研究很有必要。

然而，直升机螺旋桨和尾桨的高速转动造成载机平台偏离预定轨迹，使得雷达作用距离出现周期性波动，给SAR回波引入了高频周期性相位误差[9]。若未进行估计补偿，则在方位匹配滤波时，会出现方位重影现象[6,9]，严重影响SAR图像的质量。国内外学者针对这一问题开展了相关研究。文献[6]研究了基于相位梯度自聚集算法提取相位的高频相位补偿方法，但其运算效率不是很高，无法进行快速处理，且该方法不能拓展到全孔径数据的处理。文献[7]就直升机机载SAR对舰船的检测做了相关研究，所提方法适用于短孔径数据的频域去斜成像，却无法实现大场景的时域匹配滤波成像。文献[8]研究了基于直升机平台的调频步进频SAR成像方法。文献[9]所提方法只考虑了1个振动频点，并没有考虑多个振动频点，且在实测数据验证过程中，仅考虑了振动幅度恒定的情况，而实际情况下，直升机存在多个振动频点，且实时成像中，需在匹配滤波前完成方位重影抑制。

针对上述问题，本文提出一种基于直升机平台SAR的方位重影抑制方法。先从直升机平台振动引起作用距离周期性波动的角度出发，推导出基于直升机振动平台的SAR回波表达式，得到回波信号中正弦调制的相位项，并引入雅可比-安格尔恒等式[7]，对回波进行一阶贝塞尔级数展开，在二维频域内完成徙动校正和方位脉压处理，仿真成像结果验证了振动会引起成像时方位向重影；再从直升机SAR实测数据入手，推导出直升机平台的振动频率与自身螺旋桨和尾部推动翼的振动频率有关，并对振动频率的信息进行提取，对提取的频点信息进行积分，得到振动引起的误差相位，将多个子孔径的误差相位进行有效拼接，从而得到完整的振动误差相位。基于实测数据的处理结果验证了本文方法的有效性。

1 直升机SAR回波模型

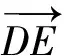
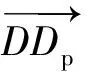
因常规直升机发动机多采用汽油发动机，发动机的转动方向与横滚方向一致，故会造成平台在横滚方向振动，从而引起以点D为中心的简谐振动[10-11]，即

r(t)=A(t)sin(wmt+φm)

(1)

式中：A(t)为振动幅度；wm为振动角速度；φm为初相；t为方位慢时间；m为第m个振动频点的编号。

由斜距历程模型(见图1)推导可得直升机平台振动情况下的瞬时斜距[12-14]，即

R(t)=[(x0-vt+r(t)sinθsinψ)2+

(2)

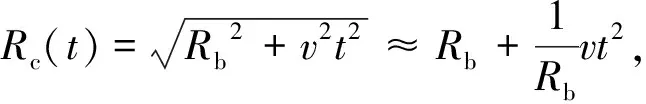
R(t)≈Rc(t)-C·r(t)

(3)

式中：C=sinβcos(α+ψ)sinθ-cosθcosβ。

以下分析信号回波特性，假设载机雷达对波束照射区域发射线性调频信号

S(τ)=ar(τ)·exp(j·(2πf0τ+πγτ2))

(4)

式中：f0为载频；γ为距离调频率；ar(·)表示距离窗；τ为距离快时间。

雷达接收到场景回波，经过下变频处理[15]，得到基频回波信号

(5)

式中：aa(·)表示方位窗；c为光速。

将式(5)换到距离频域，并进行距离脉冲压缩[16]，得到脉压后信号频域表达式为

(6)

式中：fr为距离频率。

将式(3)代入式(6)并展开，得到振动情况下的SAR回波表达式为

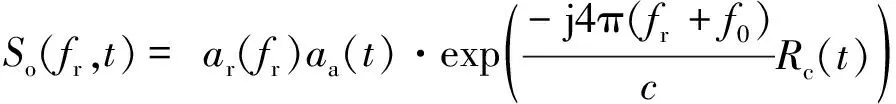
(7)

2 直升机高频振动误差分析

为更形象地描述直升机SAR实测回波数据的高阶相位误差，本文给出了5 000个方位采样点对应的相位误差幅度曲线，如图2所示。

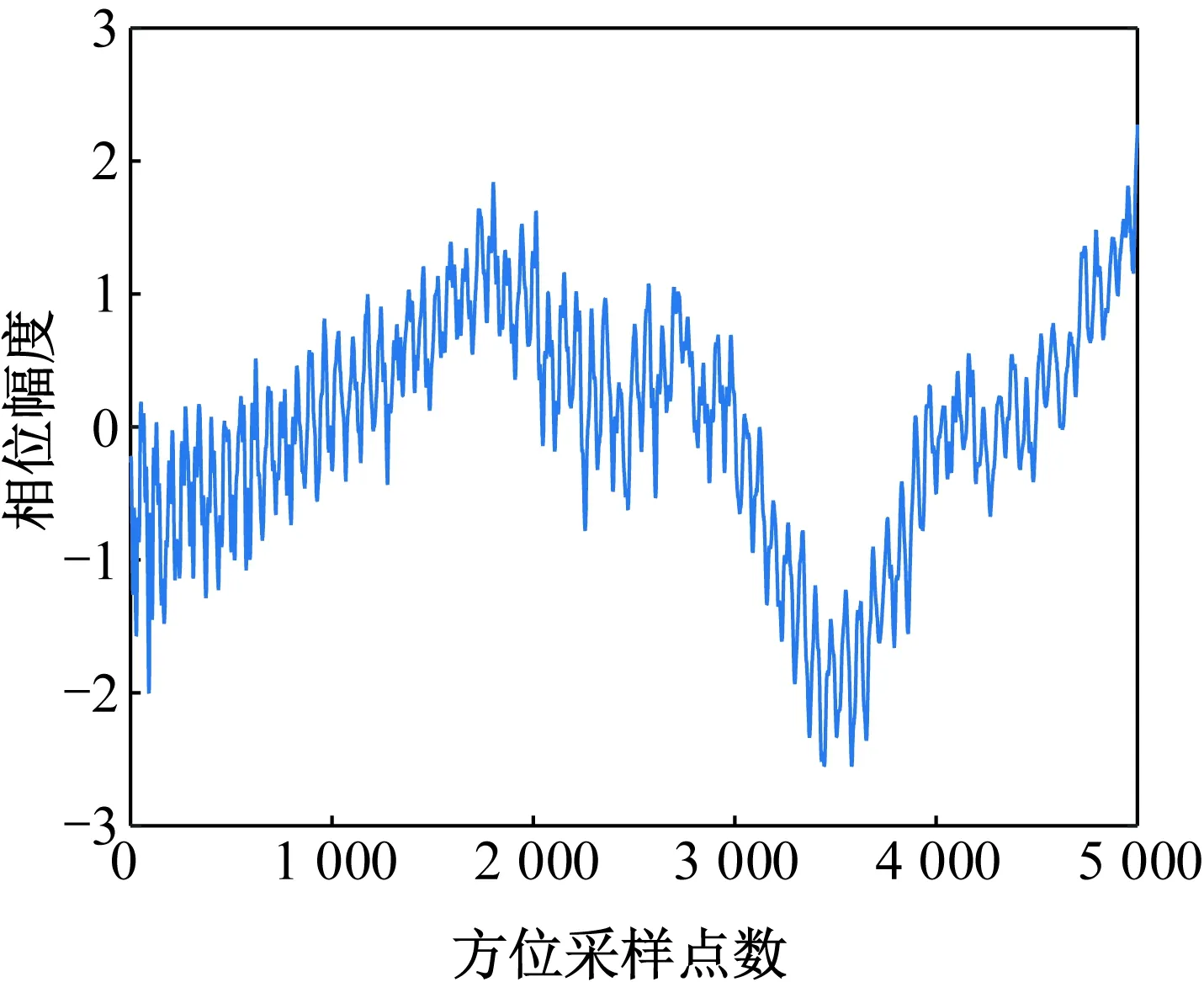
图2 信号的高阶相位Fig.2 High-order phase of echo

为深入讨论高频振动对SAR成像结果的影响，接下来对振动情况下SAR回波的多普勒中心进行分析计算，得到

(8)

由式(8)可知，多普勒中心由线性项和因载机振动而引入的正谐调制项2部分组成。为进一步分析正弦调制相位给成像带来的误差，引入雅可比-安格尔恒等式[9]对式(7)进行第一类贝塞尔级数展开，得到

So(fr,t)=ar(fr)·aa(t-t0)·

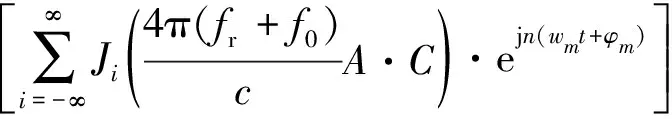
(9)

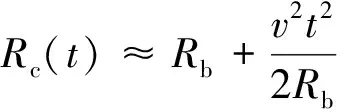
So(fr,fa)=ar(fr)exp(-j2πfat0)·

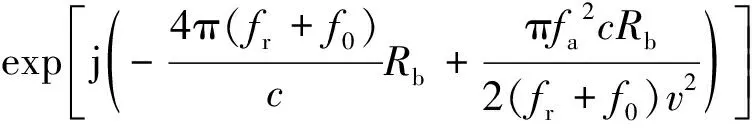
(10)

然后，在二维频域实现距离徙动校正和方位脉压处理，得到二维时域成像结果为

exp[j(2πnfmt+nφm)]

(11)

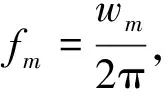
由于载机平台的振动给成像引入了高频相位误差，使得方位向出现虚假鬼影目标。主瓣两边对称分布着虚假目标回波(成对的虚假回波)，成对的虚假回波无法在时域直接滤除，这直接影响到后期的成像质量和参数估计。

3 高频振动误差估计和补偿

通过上述分析可知，虚假回波是成对出现的平台振动的瞬时幅度。虚假回波的振动频率与直升机螺旋桨和尾部推动翼的振动频率均有关，因此，无法通过时域方法直接进行估计补偿。文献[6]提出一种参数化自聚焦方法，用于提取单个振动频点的频率、幅度和初相，该方法适用于存在单个频点的情况，然而，实际直升机系统中可能存在多个频点，多个频点的频率、幅度和初相相互干扰，文献[6,9]中的方法将不再适用。因此，本文提出了一种基于时频分析的频点提取法，用于提取振动的所有频点，并利用带通滤波器对振动频率信息进行精确的滤波提取。载机振动在时频分析中表现为一个高频信号，目标回波信号和振动干扰信号的时频信息在时间轴上的投影是重合的，在时频域无法进行分离。本文在上述分析的基础上，对信号相位进行了差分处理，在差分后的相位中，发现了方位频域和相位求导域之间的关系，并从中得到振动干扰信号的频点信息。尤其要注意的是，实测数据处理过程中，直升机振动频点可能不是整数，需要进行多倍插值才能得到平台振动频点。

本文对某型号直升机平台SAR的实测数据进行了时频分析。首先对原始回波数据进行脉冲压缩处理，并完成距离单元走动、弯曲等徙动校正处理[17]，选取距离走动和弯曲校正后的散射点所在的距离单元，对其进行时频分析中的Wigner Ville(W-V)分布变换，所得结果如图3所示。从图中可以看到目标回波信号和振动信号的时频信息，目标回波信号的时频信息表现为中心的那条斜直线，振动信号时频信息表现为沿中心那条斜直线对称分布的斜直线，两者在方位时间轴和方位频域轴上的投影均重合。因此，在常规时频域里无法实现目标回波信号和振动信号的有效分离。

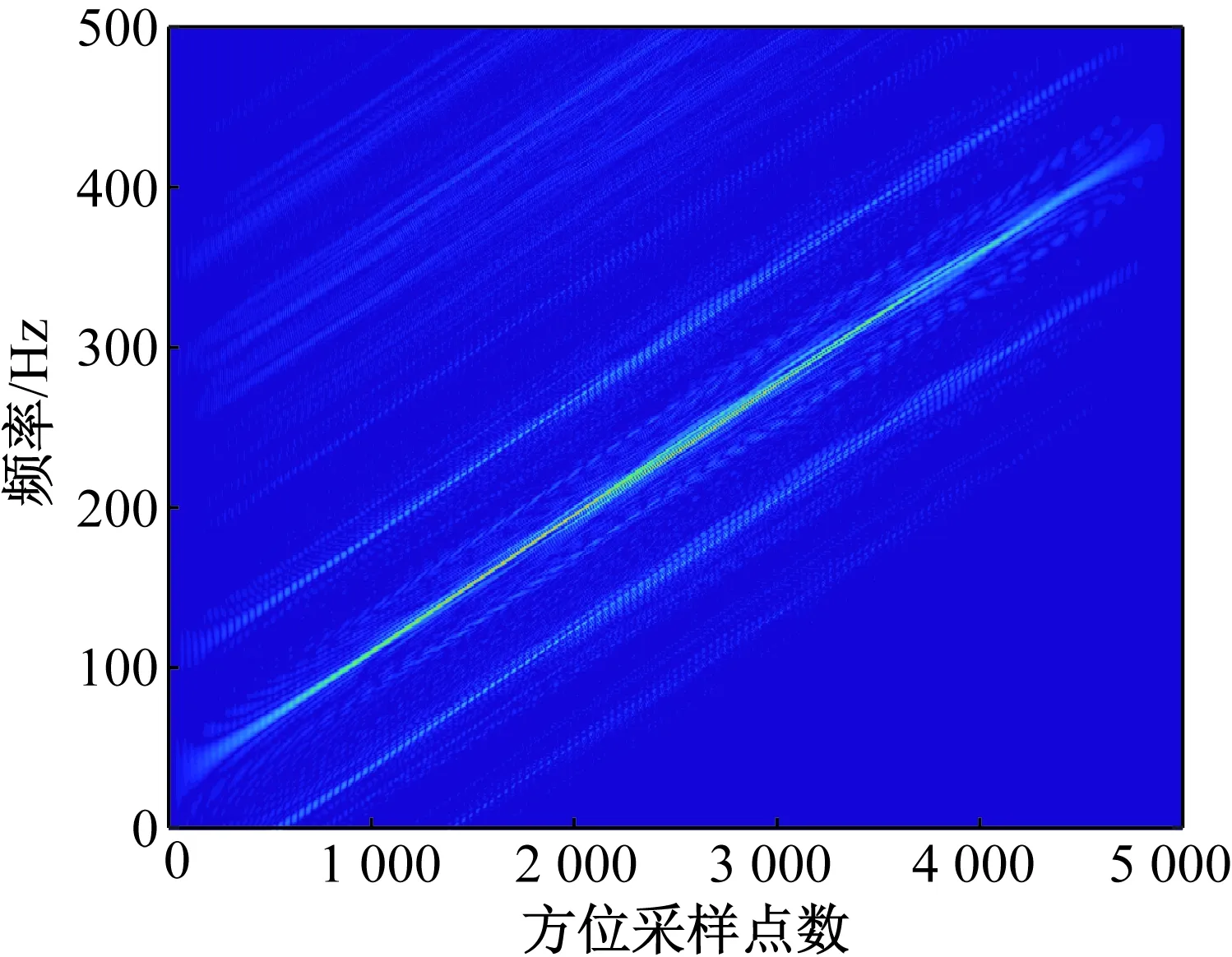
图3 补偿前目标的W-V分布谱图Fig.3 Distributed spectrum of Wigner Ville before compensation

将式(9)中距离脉压后信号变换到时域，可得

(12)

为消除Rc(t)中方位慢时间二次项对提取相位的影响，对方位信号进行差分处理，即

So(τ,t)So(τ,t-τ)*=

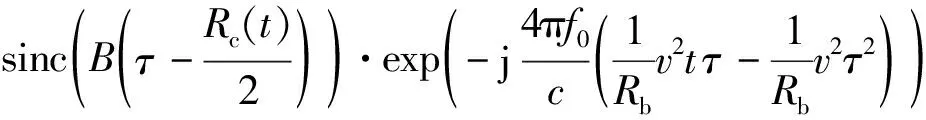
(13)

为提取得到后期的振动相位频点，利用参考文献[1]中的相位提取和解相位缠绕方法，对差分后的信号进行相位提取操作，得差分相位

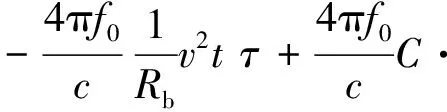
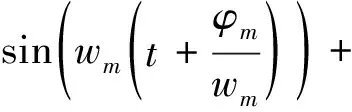
(14)

接着对差分相位sig1进行快速傅里叶变换，得到其在方位频率域的表达式为

(δ(w+wm)+δ(w-wm))

(15)

式中：wm为振动频点；fPRF为方位脉冲采样频率。由式(15)可见，sig2存在m对振动引入的虚假频点δ(w+wm)和δ(w-wm)。

利用上述推导的公式对SAR实测数据进行处理，所得结果如图4所示。由图可知，场景目标的频点在零频处，直升机螺旋桨和尾部推动翼的振动频点如图中红色圆圈处所示，其与场景目标的频点在频率轴上是分开的。

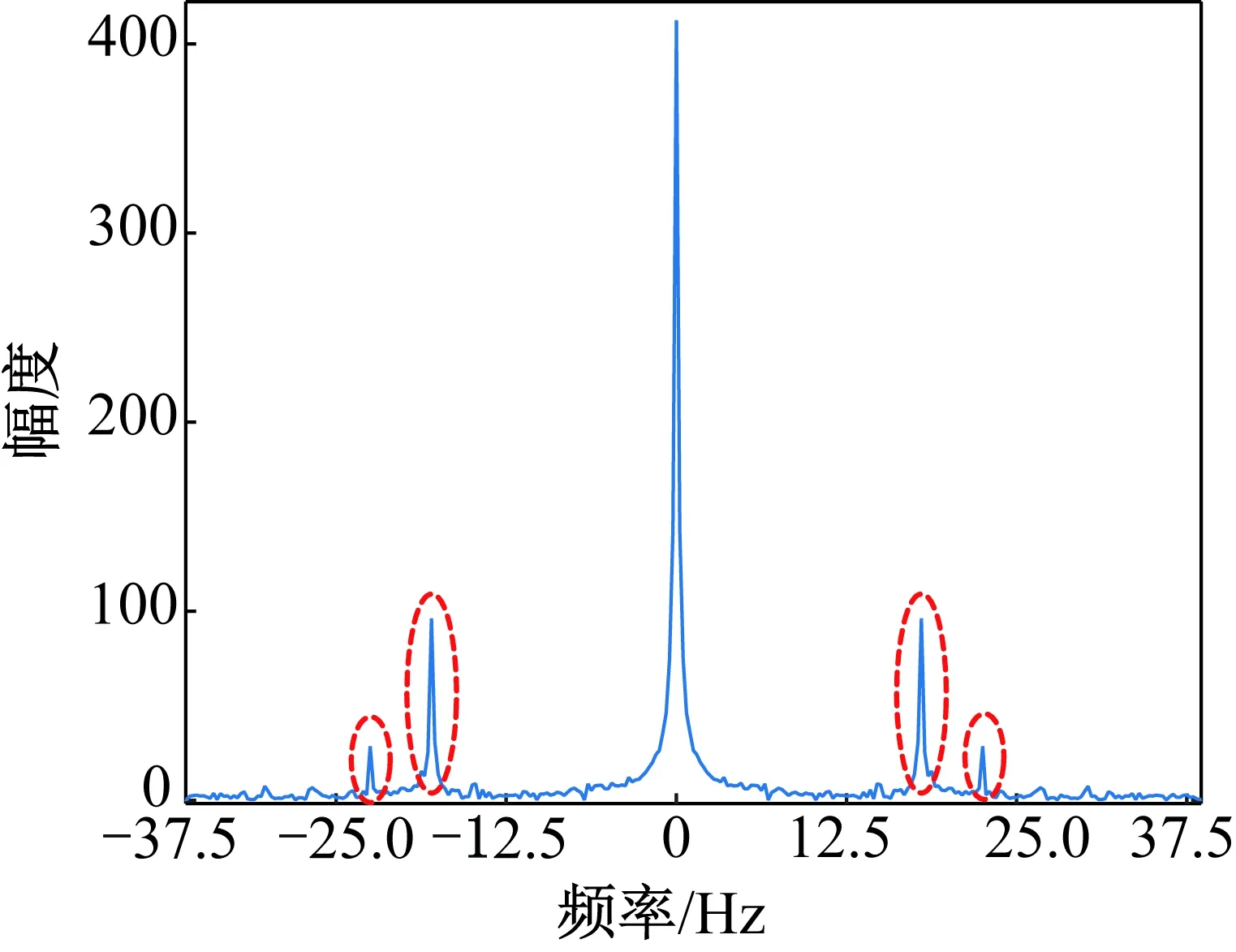
图4 直升机振动频点的信息Fig.4 Vibration frequency information

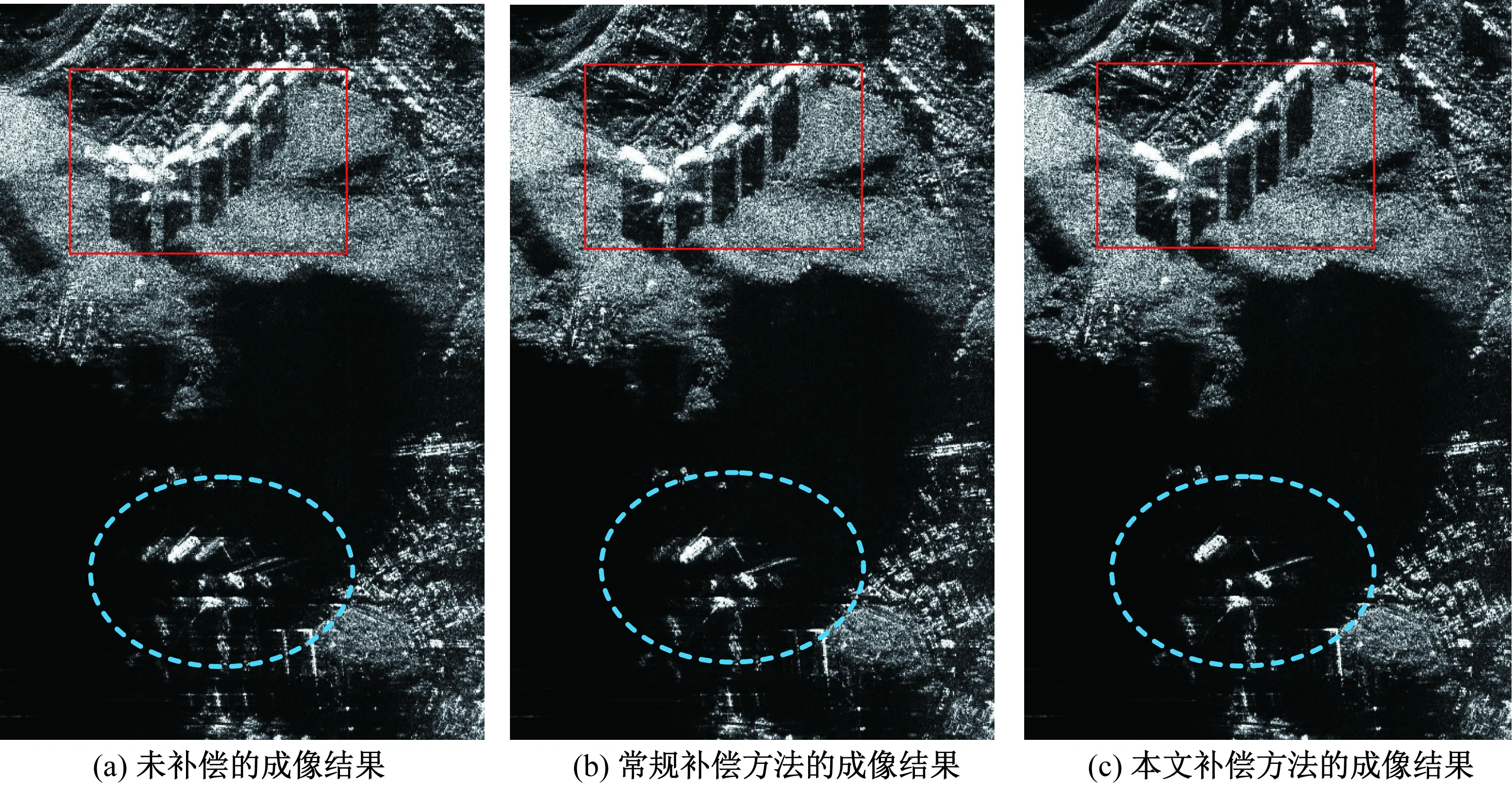
图6 高频振动误差补偿前后的实测数据结果Fig.6 Experimental results before and after high-frequency vibration compensation

本文采用带通滤波器对振动的多个频点进行提取，并对提取的振动频点的信息进行积分操作，得到振动频点的相位信息，再对原始回波脉冲脉压后的信号进行补偿，消除了高频误差项，解决了由高频误差导致的方位向重影问题。补偿后的W-V分布谱如图5所示。

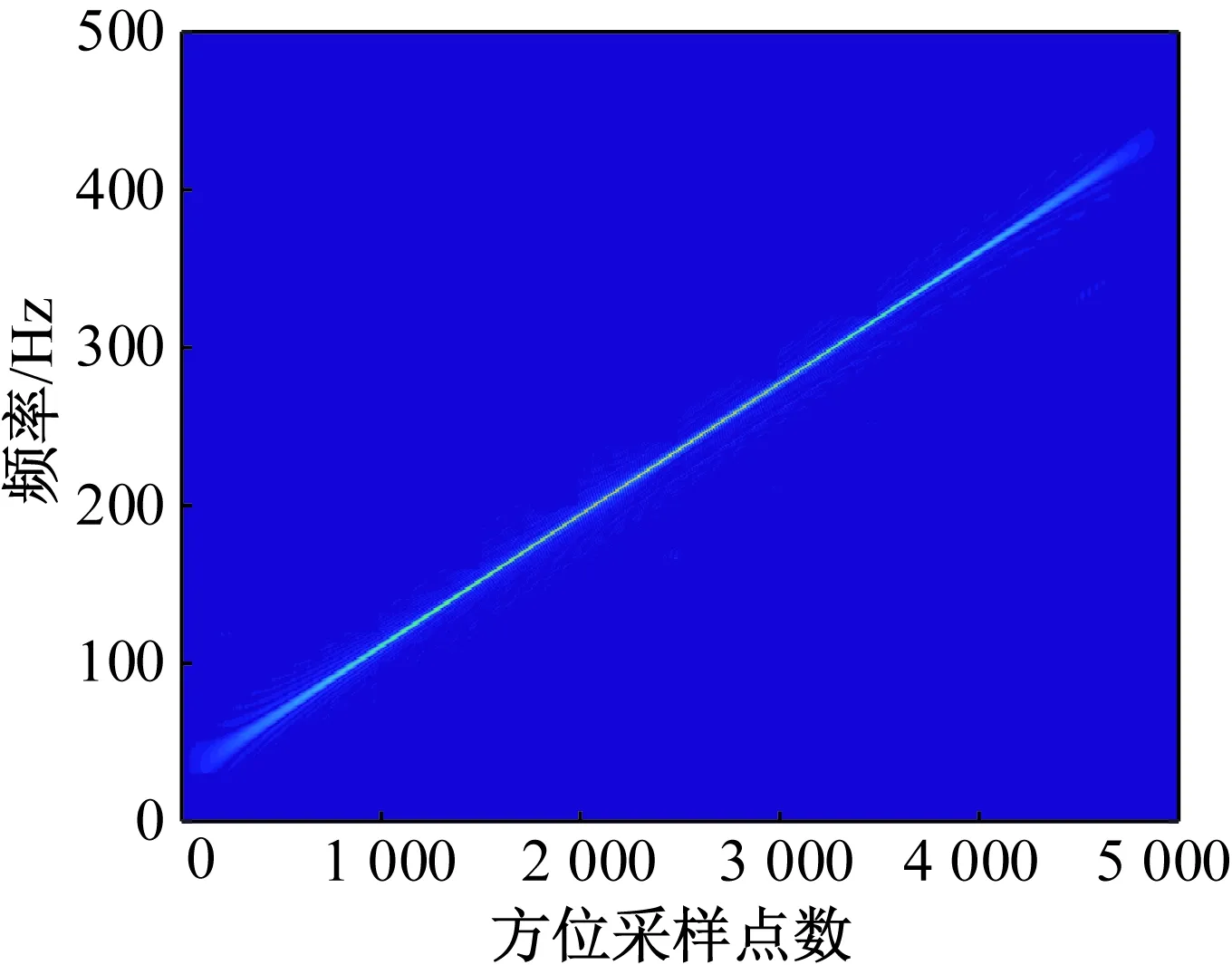
图5 补偿后的W-V分布谱图Fig.5 W-V distributed spectrum after compensation

4 实测数据处理与分析

对某型号直升机录取的实测数据进行处理，实测数据参数见表1。利用本文所提方法对数据进行高频振动相位的估计和补偿处理，在处理过程中，可以得到直升机平台的2组振动频点信息，通过计算和插值处理可知为±17 Hz和±21 Hz。

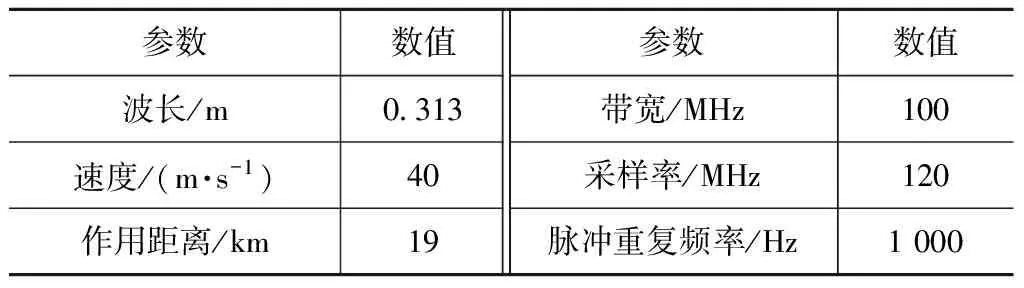
表1 实测数据参数Table 1 Parameters of real data

接下来，对得到的振动频点进行提取和积分，得到振动误差的相位，进而构造误差补偿函数，对脉压后的数据进行补偿。振动误差补偿前后直升机实测数据结果如图6所示。图中，横向表示方位向，纵向表示距离向。图6(a)为未进行振动误差补偿的成像结果，从图上方实线矩形窗和虚线矩形框中可明显看到，方位向有多组对称分布的重影；图6(b)是采用文献[6]所提常规方法估计并补偿单个振动频点后的成像结果，从图下方虚线圆圈中可看出，方位向的重影现象较图6(a)明显减弱，但仍然存在，使图像后期判读受到影响；图6(c)为采用本文方法估计和补偿2个频点后的成像结果，由图可知，方位重影问题得到了解决。

5 结束语

针对因直升机平台振动而产生成对的方位重影目标(鬼影目标)，造成图像信噪比降低的问题，提出了一种振动相位补偿算法。为消除振动引起的方位重影现象，先对直升机的振动机理进行分析，再从数据入手，估计得到载机平台的2组振动频点，利用带通滤波器提取得到振动频点信息，并对振动频点进行积分，得到高频振动相位，利用其对脉压后的回波数据进行补偿，得到无虚假回波的SAR图像。直升机SAR实测数据验证了本文方法的有效性。后续将面向直升机实时成像开展相应的工作，在实时成像过程中，直接完成对误差分量的补偿，得到方位无重影的SAR图像。