基于稀疏空间谱估计的星载SAR DBF算法

叶沙琳，张 永，杨桃丽，李 威

(1. 上海卫星工程研究所，上海 201109； 2. 电子科技大学 资源与环境学院，四川 成都 611731)

0 引言

相比于传统的光学遥感，合成孔径雷达(SAR)作为一种高性能的遥感工具，具有全天时、全天候、远距离成像的能力，并且能穿透一定深度的地表和覆盖植被进而获取大面积有效的遥感图像。因此，在战略防御、地形测绘等军用和民用领域，SAR有着广泛的应用。然而，传统星载单通道SAR存在最小天线面积限制[1]：高方位分辨率和宽距离测绘带是一对不可调和的矛盾量，高方位分辨率要求高脉冲重复频率(PRF)，而宽距离测绘带则要求低PRF。为了解决传统星载单通道SAR方位高分辨和宽距离测绘带的矛盾，国内外学者们提出了结合数字波束形成(DBF)的多通道(MC)技术[2-8]。其中，利用距离多通道可实现距离模糊抑制，从而实现距离宽测绘带成像，也可用来提高系统信噪比(SNR)。

SUESS等[3]提出的俯仰向波束扫描(SCORE)技术利用小天线发射宽波束信号覆盖宽测绘带，然后结合DBF技术，利用多个接收通道形成等效的高增益窄波束沿距离向扫描接收回波。但是，该成像系统受地形高程的影响，导致波束指向产生偏差，从而造成目标信号分量损失。当发射信号的脉冲宽度较长时，脉冲覆盖范围将超出接收波束的宽度，造成接收增益损失及SNR降低。

针对以上问题，李杨等[9]研究了4种适用于不同发射信号带宽的距离向DBF处理方法。齐维孔等[10]分析了卫星滚动角对距离DBF的影响，提出利用宽零陷技术抑制距离模糊。冯帆等[11]提出了一种将零点指向空域滤波和FIR时域滤波相结合的方法，解决了脉冲空域延展和距离模糊的问题[12]。韩晓东等[13]提出距离向两级DBF加权处理方法来抑制距离模糊。王伟等[14]分析了基于距离DBF的理想情况下的SAR系统性能，包括噪声等效后向散射系数(NESZ)和距离模糊信号比(RASR)。但是，这些方法均未考虑地形起伏的影响。当地形高程起伏不可忽略时，以上方法将导致波束指向产生偏差，损失目标信号分量，增加模糊分量。

为了降低地形起伏的影响，BORDONI等[15]提出在星上对各通道接收回波分别进行距离压缩和配准后，再利用MUSIC等子空间类空间谱估计方法来获取回波信号等效的波达方向，从而缓解地形高程对波束指向的影响。冯帆等[16]和刘尧等[17]也提出了类似的方法，对接收回波信号进行距离压缩后，利用子空间谱估计方法来改善地形高程的影响。HE等[18]提出将各通道接收回波下传至地面系统后，利用MUSIC等空间谱估计方法来估计回波信号的波达方向，从而缓解地形变化对波束形成的影响。然而，这些星上处理方法对实时处理的要求很高，会极大增加星上的处理量和系统实现难度。此外，由于采用子空间类测向方法，必然受到样本数和SNR的影响。当样本数较少或SNR较低时，波达方向的估计性能将大大下降。KRIEGER等[19]针对地形高程对距离模糊抑制的影响，提出了在忽略地形高程对目标信号分量损失的影响的前提下，先利用SCORE技术对各子测绘带回波进行扫描接收，然后将数据下传至地面系统，再结合自适应波束形成的方法，利用各子测绘带的回波实现距离模糊抑制。该方法理论上可在不增加星上系统复杂度的前提下，实现距离模糊抑制。但是，当地形高程变化较大时，SCORE技术造成的目标分量损失将不可忽略，此外自适应的波束形成方法也会受到小样本和低SNR的影响。

本文提出了一种基于稀疏空间谱估计的星载合成孔径雷达数字波束形成的方法。该方法将目标场景高程估计问题转换为稀疏空间谱估计问题，降低了现有方法易受小样本和SNR约束影响的限制。

1 处理算法

本文方法的处理流程如图1所示，主要包括距离压缩、波达方向估计和波束形成。

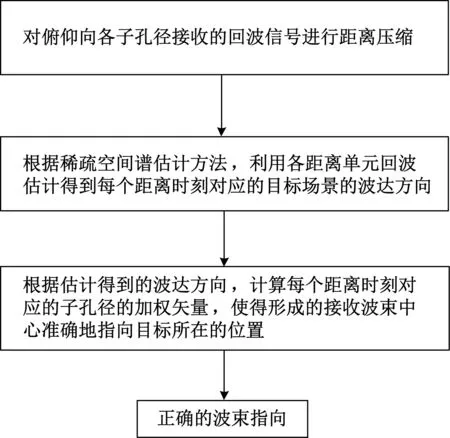
图1 基于稀疏空间谱估计的DBF实现过程Fig.1 Process of DBF based on sparse spatial spectrum estimation

1.1 距离压缩

假设SAR系统的整个天线阵面沿俯仰向均匀划分为M个子孔径，如图2所示。

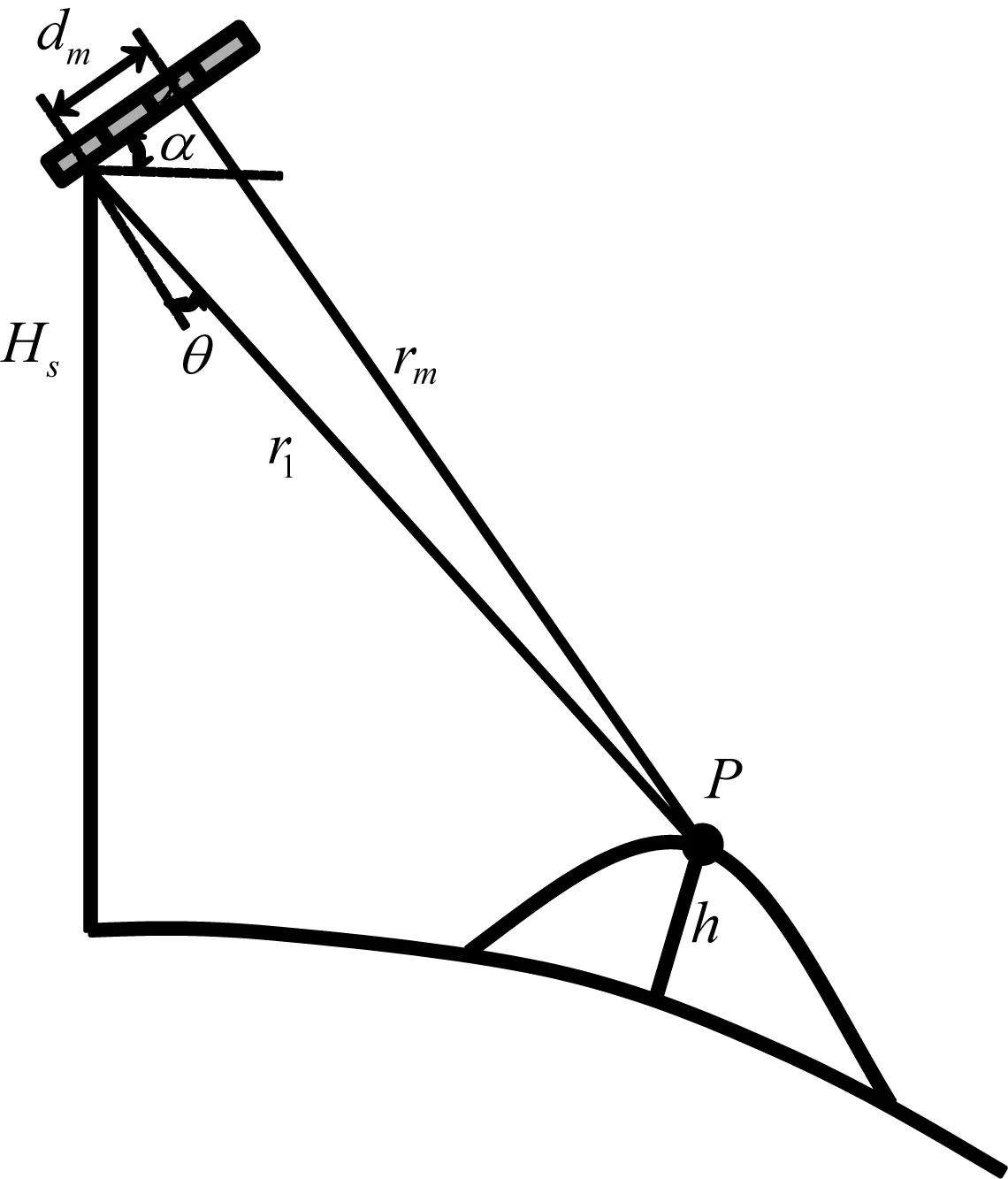
图2 SAR系统在俯仰向的观测几何示意图Fig.2 Geometrical diagram of SAR system in elevation

图中：Hs为卫星平台高度；dm为第m个子孔径到第1个子孔径的距离；α为天线水平倾角；r1和rm分别表示地面目标P至第1个和第m个子孔径的斜距；h为目标P的海拔高度；θ为目标至第1个子孔径的斜距连线与天线面板法线的夹角，其值离开天线法线向上为正，向下为负，可由式(1)计算得到，即

θ=

(1)

式中：Re为地球半径。

根据成像几何关系可得

(2)

由于天线尺寸相比目标斜距来说非常小，因此式(2)可近似为

rm≈r1-dmsinθ

(3)

假设第1个子孔径发射信号，所有子孔径同时接收回波信号。考虑加性白噪声且仅考虑距离向回波，第m个子孔径接收的回波信号进行距离压缩后可写为

(4)

式中：σ为目标后向散射系数；τ为距离快时间；pr(τ)为压缩脉冲包络，对于矩形窗来说，pr(τ)为sinc函数；c为电磁波传播速度；fc为发射信号载频；n(τ)为高斯白噪声。当dmsinθ的大小相对于分辨率来说不可忽略时，可对各子孔径接收回波相对第1个子孔径进行配准，则式(4)可改写为

sm(τ)=

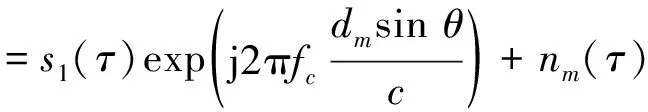
(5)

其中

(6)

经过距离压缩后，接收的回波信号能量将主要集中在1个距离门内。将各子孔径接收回波用矢量形式表示为

s(τ)=s1(τ)p(θ)+n(τ)

(7)

其中

s(τ)=[s1(τ),s2(τ),…,sM(τ)]T

(8)

(9)

n(τ)=[n1(τ),n2(τ),…,nM(τ)]T

(10)

1.2 波达方向估计

根据稀疏空间谱估计方法，利用各距离单元回波可估计得到每个距离时刻对应的目标场景的波达方向。考虑回波信号的空域稀疏性，忽略快时间变量τ，将距离向回波信号构建为

(11)

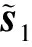
(12)

式中：θq的取值范围为雷达波束的照射范围，q=1,2,…,Q。

一般来说，Q>M，因此可将目标场景的波达方向估计问题转换为以下稀疏问题[20]，即

(13)

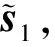
1.3 波束形成

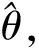
(14)

式中：上标*表示取共轭。

在实际应用中，目标场景地形变化缓慢且连续。为了降低运算量，可对距离向回波进行分块，选取每块场景中的某一距离单元估计得到波达方向，再根据波达方向和斜距估计出每块场景的地形高度，然后利用估计得到的各块距离向的地形高度拟合出整个场景的高度，最后再根据几何关系求解得到所有距离单元所对应的波达方向。下面结合仿真数据实验对稀疏空间谱估计法的效果做进一步的说明。

2 仿真实验验证

为了验证所提方法的有效性，利用计算机仿真数据进行实验验证。星载SAR系统的仿真参数如表1所示，其中俯仰向天线尺寸总长为1.5 m，并沿俯仰向均匀划分为15个接收子孔径，即单个子孔径长度为0.1 m。俯仰向天线方向图为|sinc|形式，并假设在场景中心有一点目标，目标斜距为615.95 km。

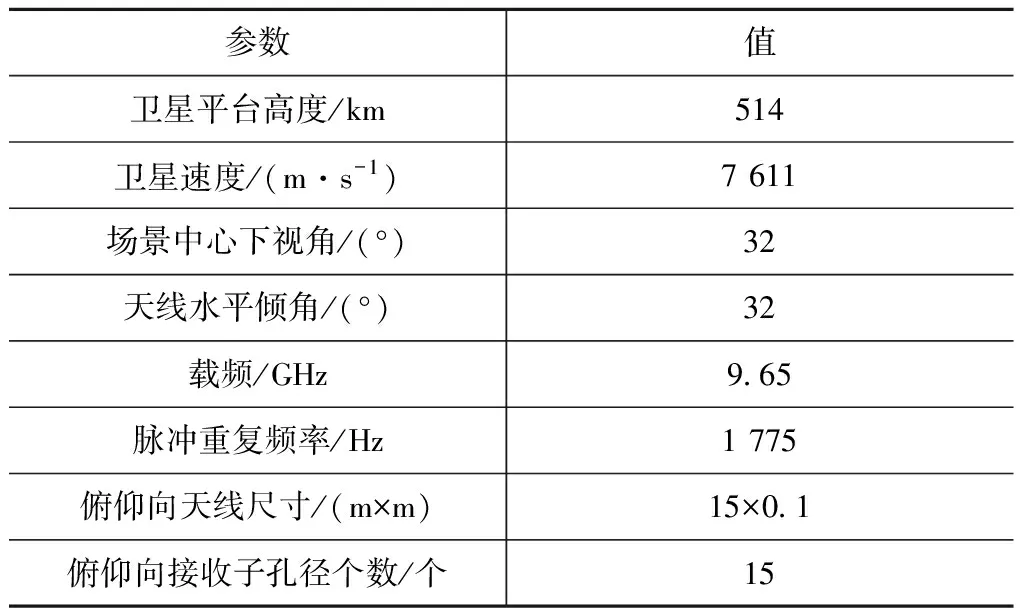
表1 仿真参数Tab.1 Simulation parameters

对各子孔径回波信号进行距离压缩后，选取目标所在的距离单元作为估计样本。图3(a)和图3(b)分别给出了在不同目标海拔高度的情况下，利用SCORE法和本文所提的稀疏空间谱估计法所引入的波束指向偏差和相应的接收增益损失。当目标海拔高度为0时，目标下视角为32o，结合天线水平倾角可得目标相对天线阵列的波达方向角为0。随着目标海拔高度的变化，相应的波达方向角也会发生变化，而传统SCORE法不考虑目标海拔高度，依然采用平地曲面模型，将导致所估计的目标波达方向发生偏差。随着目标海拔高度的增加，利用SCORE法得到的波束指向偏差也越来越大，波束指向偏差导致波束增益损失(图3(b))；而采用本文方法得到的目标波达方向几乎不随着目标海拔高度的变化而变化，即几乎不存在波束指向偏差和波束增益损失。

与传统自适应法相比，本文提出的方法受SNR的影响较小。图4和图5分别给出不同SNR时，利用本文方法和传统自适应法估计得到的目标空间谱分布。假设海拔高度为0，可得目标相对天线阵列的波达方向为0。从图4和图5中可看出，当SNR为0时，两个方法均能正确估计得到目标的波达方向，而当SNR降低为-10 dB时，本文方法也能正确估计出目标的波达方向，传统自适应法却因噪声的影响，使目标空间谱受到干扰，影响了目标波达方向的估计。

综上可知，在考虑目标海拔高度的情况下，相较于SCORE方法，本文所提方法在波束指向和增益损失方面都有更好的性能；同时，相比于传统的自适应法，本文所提方法受SNR的影响较小。

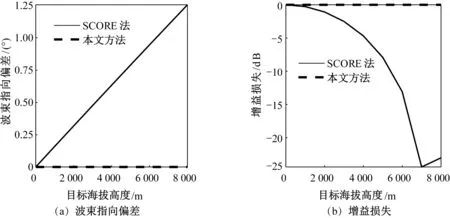
图3 两种方法仿真结果Fig.3 Simulation results of two different algorithms

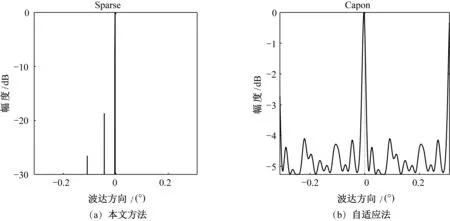
图4 两种方法的空间谱估计结果(SNR为0)Fig.4 Estimated spatial spectrum of two different algorithms with SNR of 0

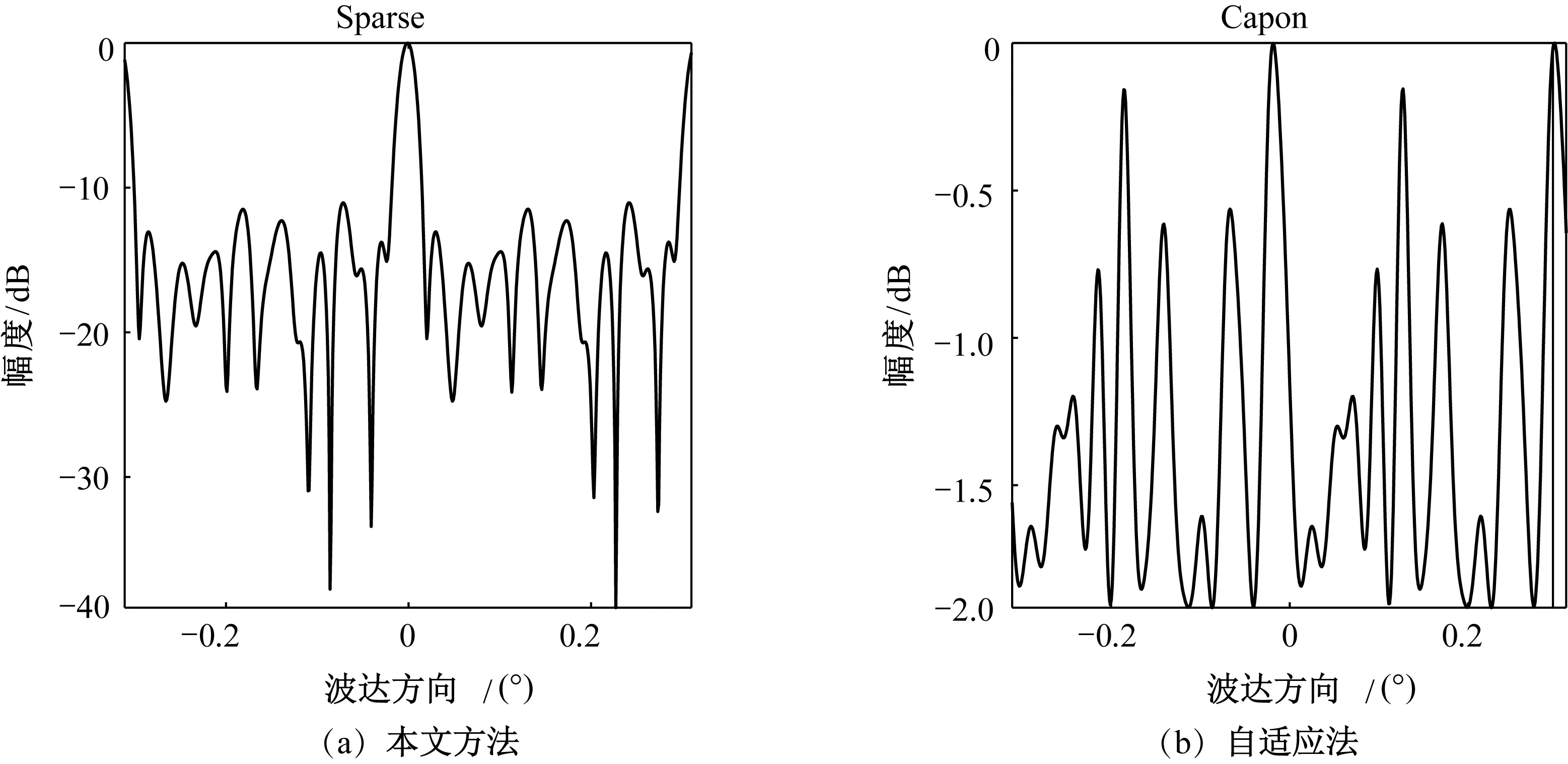
图5 两种方法的空间谱估计结果(SNR为-10 dB)Fig.5 Estimated spatial spectrum of two different algorithms with SNR of -10 dB

3 结束语

传统SCORE技术受地形影响，在进行接收波束扫描时将出现波束指向偏差，导致波束增益损失，而传统的自适应法受回波SNR影响较大。为解决以上问题，本文提出了一种基于稀疏空间谱估计的星载SAR数字波束形成方法，该方法将目标场景高程估计问题转换为稀疏空间谱估计问题，然后通过估计得到的目标波达方向形成正确的波束指向，从而实现高分辨SAR成像。最后，通过仿真实验验证了本文方法的有效性。