浅析基于逻辑推理能力发展的高中数学核心素养培养

李新岳

摘 要：逻辑推理能力是高中数学学科核心素养的重要组成部分，是从命题出发依据逻辑规则推导出另一个命题的过程。逻辑推理的过程主要以归纳、演绎为主，根据命题的内容不同选用不同的推理方法。在高中数学教学领域，学生能够通过逻辑推理的过程，利用现有数学知识验证新的数学知识，从而有效地构建知识体系，帮助学生养成良好的逻辑思维能力。

关键词：高中数学;逻辑推理能力;核心素养

逻辑推理能力作为高中数学学科核心素养的重要组成部分，不仅能够有效地引导学生加强对数学知识框架的掌握，更能够使学生获得数学学科之外的逻辑思维能力发展。几何证明教学对于发展学生的逻辑推理能力有至关重要的作用。在几何证明教学中，学生通常需要利用现有的几何知识，通过归纳与演绎，去证明新的几何命题。在这个证明过程中，对于命题的证明步骤有严格的要求，需要学生根据现有条件以及自身的几何知识进行逐步的论证与判断。

一、基于逻辑推理培养学生合情推理和演绎推理相结合意识

波利亚在如何解题上有其独到的见解，他特别关注在解题或证明问题时发现简单的类比题，类比题的发现可以引导解题者顺利解决原题是他一直持有的观点。根据不同对象的特性、属性、关系等方面的相同或相似之处进行其他方面的推理，这种推导其他可能相同或相似的思维形式的过程即为类比推理。对于具体的证明解题过程而言，我们注重在学生审题环节中，引导学生先利用“合理推理”得出结论，再运用“演绎推理”的手段严格地证明，培养学生“合情推理”和“演绎推理”相结合意识。

例1.平面几何中的勾股定理如下：设△ABC的AB，AC互相垂直，则AB2+AC2=BC2，将其拓展到空间，研究三棱锥的侧面面积和底面面积之间的关系时也可将其进行类比，可得以下正确结论：设三棱锥A-BCD的三个侧面△ABC、△ACD、△ADB两两相互垂直，则 。

勾股定理的证明方法也同样可以在此处进行类比。教师在学生练习时应该引导学生养成预估解题思路能解性的习惯，再进行严格的演绎推理。

二、利用自主证明解题的过程发展学生的逻辑推理能力

几何证明教学能够有效地培养学生的逻辑推理能力，通过引导学生对命题条件的归纳以及演绎，可以使学生按部就班地推导出相应的结论，利用学生自主证明的解题过程，引导学生加强逻辑推理能力，获得良好的教学效果。具体教学过程见例2。

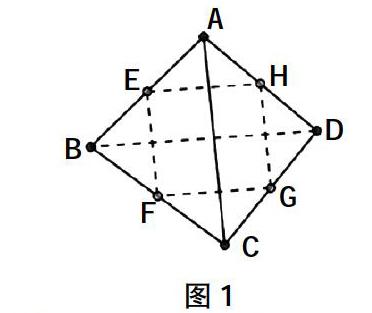
例2.如图1所示，已知在空间四边形ABCD中，E，F，G，H分别是边AB，BC，CD，DA的中点，求证：EFGH是平行四边形。

在这道题的证明解题过程中，我首先引导学生复习空间四边形与平行四边形的基本性质及空间中两条直线平行的判定定理，之后引导学生证明：“在空间四边形ABCD中，因为E，H分别是AB，AD的中点，∴EH∥BD，EH=BD;同理，FG∥BD，FG=BD，所以EH∥FG，∴EH=FG，所以四边形EFGH为平行四边形。”这道题训练了空间两条直线平行判定定理的运用。通过这样的解题教学模式，能够使学生将几何相关的理论知识与应用相结合，从而有效发展了学生的逻辑推理能力。

三、通过思辨论证训练培养学生的逻辑推理能力

立体几何内容是培养学生空间想象能力和逻辑推理能力的重要载体，通过对直线与直线、直线与平面、平面与平面的位置关系的证明，着力培养逻辑推理能力。通过寻找位置关系成立的要素，往往采用分析方法，逐步完成，就能顺利解答。

例3.如图2所示，在四棱锥ABCD中，底面ABCD是菱形，∠BAD=，PA=PD，F为AD的中点，PD⊥BF。若E在线段BC上，且EC=BC，（1）求证AD⊥PB;（2）能否在棱PC上找到一点G，使平面DEG垂直平面ABCD？并证明相应结论。

（1）略

（2）在此小题的探究过程中，我首先启发学生，假设在棱PC上存在一点G，使平面DEG⊥平面ABCD，平面DEG内一定存在与平面ABCD垂直的直线，若存在此直线，则只要在平面DEG中找到该直线。若平面DEG中没有垂直于平面ABCD的直线，则必须在平面DEG内作出与平面ABCD垂直的直线。由AD⊥BF，PD⊥BF，可证BF⊥平面PAD，平面ABCD垂直平面PAD。又AD⊥PF，所以PF⊥平面ABCD。如图3，联结FC交DE于点Q，过Q作QG∥PF交PC于G，点G即为所要找的点，根据条件可得GC=PC。通过这样分析、综合法兼具的探索过程，有效地让学生利用分析、综合法这两种演绎推理探究比较复杂的证明题。

总而言之，邏辑推理能力既是学生在数学学习过程中的关键能力，同时也在学生的终身发展过程中发挥着至关重要的作用。在教学过程中，基于例题的解答基于解题教学对学生进行逻辑推理能力培养，使学生在解题证明的过程中，在发展了自身数学学科核心素养的同时，有效培养自身的逻辑推理能力，获得更好的学习效果。

参考文献：

[1]陈玉娟.例谈高中数学核心素养的培养：从课堂教学中数学运算的维度[J].数学通报，2016（8）：34-36.

[2]王雅琴.刍议高中数学核心素养的教育价值及教学渗透策略[J].张家口职业技术学院学报，2018（1）：79-80.

编辑 谢尾合