中学数学中概率的相关概念辨析
——从一道高考题谈起
赵 轩 任子朝
(教育部考试中心 100084)
1 引言
2018年高考全国Ⅰ卷第20题是一道概率统计大题,该题目内容如下:
某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验.设每件产品为不合格品的概率都为p(0 (1)记20件产品中恰有2件不合格品的概率为f(p),求f(p)的最大值点p0. (2)现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的p0作为p的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用. (i)若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为X,求EX; (ii)以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验? 这道题是试卷中难度较高的一道大题,题目涉及的知识范围较广,包括独立重复试验概率模型、二项分布的概念和应用、概率的计算、函数求导、随机变量的数学期望的计算与应用、统计中参数的估计等.这道题综合考查了很多概率知识,考查内容丰富,题目文字量较多,难度相对较大,因此在考后受到高校概率专家和中学教师的广泛关注,并引发了讨论.本文通过对题目进行分析和解读,对于其中涉及到的一些概率与统计的基本概念进行辨析,就中学教学中概率相关知识的一些问题进行说明,以期助力中学概率与统计知识的教学与高考对相关内容的考查. 大多数人对于概率这个概念的直观认识是:概率就是一个事件发生的可能性大小,这种认识符合初学者的认知水平,也是传统概率论的出发点之一.上世纪30年代,随着测度论的产生和发展,人们对于概率的认识更加深入,前苏联数学家Kolmogorov在此基础上建立了现代概率论的公理化体系.“概率”这个概念也有了明确而具体的定义. 由定义1可以看出,集合S上的任何一个σ-代数都是S的幂集(S的幂集是由S的所有子集组成的集合,记作2S,即2S={A|A⊆S})的一个子集,特别地,S的幂集也是集合S上的一个σ-代数(S的幂集也称作S上的离散拓扑,表示S上最细的拓扑结构).对于集合S而言,其上的任何一个σ-代数都是对S的结构的一种刻画,在此结构下,这个σ-代数中的元素称为可测集. 在中学概率统计部分的教学中,我们所处理的都是有限集,一般把一个试验的所有可能结果的全体称为这个试验的样本空间,样本空间的任意子集称为一个事件,样本空间中的元素(即试验结果)称为样本点.需要说明的是,大学教材中对于事件的定义是样本空间的可测子集,由于中学生没有可测集的概念,因此在中学教学中定义为样本空间的任意子集,那么按照这个定义,如果把样本空间记为S,所有事件的全体构成的集合就是2S. 通过以上定义,我们得到了一个三元组(S,Ω,P),这个三元组就称为一个概率空间.其中S代表样本空间,Ω是S中可测集的全体(更具体地说,Ω中的任意一个元素都是S的可测子集,从而是一个事件,因此Ω是所有事件构成的集合),P为S上的概率.值得注意的是,概率并不是对于所有子集均有定义,而是定义在所有可测集(事件)之上.在中学阶段的教学中,可以省略对于可测集的说明,认为S的所有子集都是可测的,这时三元组(S,Ω,P)中的Ω=2S,可把概率空间定义中的三元组简化为二元组(S,P).从定义可以看出,所谓概率就是一个函数(更准确的说是一个测度),定义在所有事件的集合之上,描述了事件发生的可能性大小. 对于解决概率问题而言,很重要的一点是能够正确认识和理解其中的概率空间,特别是样本空间.以本题为例,“每件产品为不合格品的概率都为p(0 另外需要指出的是,产品在生产出来后,合格或不合格就已经确定,其是否合格的状态是一个确定的试验结果,而不是样本空间.也就是说,生产一件产品有两个可能的结果(样本空间),抽查一件产品检验只有一种结果(试验结果,即样本空间中的一个样本点).但在没有检验前,并不能判断其是否合格.我们可以类比地考虑下面的问题:(1)一个盒子里一个正在转动的硬币落地时出现正面的概率;(2)盒子里硬币落地后,在还没看到的情况下,猜它是正面的“概率”.由于无法判断结果,因此可以认为两个问题中的“概率”是一致的.同理,在本题中,“每件产品为不合格品的概率都为p(0 大学概率论教材中对于随机变量的定义也是公理化的,其中有些概念超出了中学生的知识范围,但对于中学教师来说,应该有所了解. 定义3设(S,Ω,P)是一个概率空间,若X是S上的一个实值可测函数,则称X为S上的一个随机变量. 从定义中可以看出,随机变量是一个定义在样本空间上的函数,随机变量本身既不“随机”,也不是变量.随机变量的“随机性”体现在概率P的分布之中.关于样本空间也存在类似的理解误区,样本空间是试验结果的全体,里面的元素不是随机的,随机体现在抽取这些样本是“随机”的,这是一个描述,不是一个定义. 值得注意的一点是,题目第(2)问中“现对一箱产品检验了20件,结果恰有2件不合格品”这个条件即不是对样本空间,也不是对随机变量的描述,而是给出了一个确定的检验结果(试验结果),这个试验结果是样本空间S1×S2×…×S20中的一个元素(样本点).此外在统计中,“检验20件产品恰有2件不合格”可理解为对频率的一种描述,一般来说检验结果中不合格品出现的频率与产品制造时不合格的概率可以不相同.在本题第(2)问中“对一箱产品检验了20件,结果恰有2件不合格品”的概率与制作20件产品恰有2件不合格的概率是相同的,因此“以(1)中确定的p0作为p的值”体现了极大似然估计的思想. 我们知道,在概率空间(S,Ω,P)中,两个事件A,B独立的定义是P(AB)=P(A)P(B).讨论事件独立性的前提是所有事件都包含在同一个概率空间中.事件独立不应简单地直观理解为两个事件之间没有关联,事件的独立性可以理解为一种比例关系. 值得注意的是,在随机变量独立性的定义中,所有随机变量都定义在同一个概率空间上.对于定义在不同概率空间上的随机变量,若要讨论其独立性,需要将它们统一到同一个概率空间中,即在它们所在的概率空间的乘积空间上进行讨论. 在本题中,“每件产品为不合格品的概率都为p(0 基于上述讨论,可以给出本题的一种解答: 令f′(p)=0,得p=0.1.当p∈(0,0.1)时,f′(p)>0;当p∈(0.1,1)时,f′(p)<0.所以f(p)的最大值点为p0=0.1. (2)由(1)知,p=0.1. (i)令Y表示余下的180件产品中的不合格品件数,依题意知Y~B(180,0.1),X=20×2+25Y,即X=40+25Y. 所以EX=E(40+25Y)=40+25EY=490. (ii)如果对余下的产品作检验,则这一箱产品所需要的检验费为400元. 由于EX>400,故应该对余下的产品作检验. 如对本题中的概率空间(样本空间)没有正确的理解,混淆了定义,可能会导致解题中出现错误,例如,一种典型的错误就是误用超几何分布进行计算.事实上超几何分布中三个参数N,M,n的含义可以理解为:已知N件产品中有M件不合格品,不放回的抽取n件时,其中的不合格品个数k的分布;本题中事先并不知道一箱产品中不合格品的总数,因此不应使用超几何分布进行描述. 部分教师认为“每件产品为不合格品的概率都为p(0 对于统计类题目来说,答案往往存在一定开放性,对同一个问题,可能有多种理解角度,能够采用不同的统计方法,而不同统计方式可能产生不同结果.本文中给出的是基于生产实际的一种解法.事实上,在实际生产中,面对大批量产品时,产品检验都是成批次进行,题干中也给出了“根据检验结果决定是否对余下的所有产品作检验”这条说明,因此,在上述解答过程中产品检验只分两种情况讨论:要么对余下产品都进行检验,要么都不检验,不存在第三种情况. 今年高考全国I卷第20题综合考查了概率与统计的基础知识和基本思想方法,以及学生综合应用所学的概率与统计知识分析问题、解决问题的能力.试题设计较新颖,蕴含了极大似然估计的统计思想,情境熟悉而不落俗套,具有一定难度,有较好的选拔功能.正确理解此题,需要学生能够正确掌握概率、随机变量、独立性等定义,了解独立重复试验概率模型、二项分布等概念和应用范围,并能将所学知识灵活运用.本题强调了对于基本概念的考查,对于中学教学具有很好的导向作用,引导概率统计教学回归教材、重视概念. 在中学阶段,学生仅具备初等数学的基础,因此概率、统计上的许多概念,其公理化的严格定义很难让中学生理解并接受,但作为中学教师应该正确理解,并在教学过程中根据严谨性和量力性原则进行直观的解释,而不是错误的解释.特别是不能混淆概率中的概念和统计中的概念,比如概率和频率,在教学中可以将此类概念进行对比说明.此外,还应突出重要概念的实际意义,突出用概率、统计方法解决问题的基本思想,突出知识的综合应用,通过实际问题加深学生对于概念的认识.让学生将抽象的概念与具体的生活实际相结合,从而帮助其进一步理解这些概念的深层次内涵. 在中学概率与统计部分的教学中,比较容易出现重视做题忽视概念教学的情况,更加注重对各种题型的解法技巧训练,而忽略了对基本概念的理解.但对于知识的内化和迁移,则需要建立在对概念深刻理解、灵活应用的基础之上.中学阶段所学的这些基本内容在大学阶段的进一步学习中将起到极其重要的作用,是深入学习和理解后续数学知识的基石,因此中学教学中应该进一步强化概念基础,强调对于知识和概念本质的理解.高考作为高校选拔新生的测试,今后也应进一步加强基本概念考查,对中学教学发挥积极的导向作用,引导中学注重基本概念、基本原理的教学,打破机械刷题的学习模式.2 概率

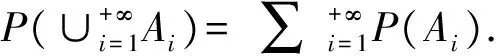
3 随机变量

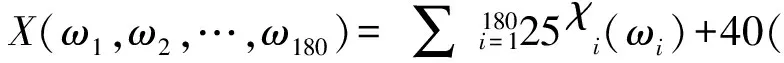
4 独立性
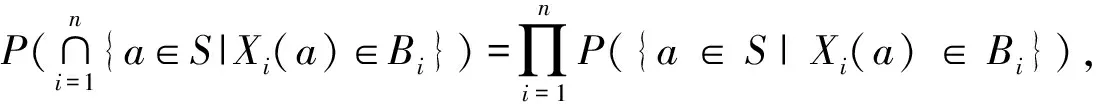
5 关于解答的一些补充
6 小结

