一种限定混沌状态变量运动区域的方法*

赵柏山，刘晓晓，张学松

(沈阳工业大学 信息科学与工程学院，沈阳 110870)

自20世纪60年代Lorenz发现了第一个混沌系统以来，混沌理论的研究和应用在物理学、生物学、信息科学等许多领域得到了广泛关注.Lorenz系统在混沌学的形成和发展中起到了不可替代的作用，因而成为后人研究混沌系统的基点.以Lorenz系统为基础，研究者们提出了各种新型混沌系统，如基于电流反馈运算放大器的忆阻混沌电路系统[1]、基于混沌系统部分序列参数辨识的混沌保密通信系统[2]、基于分数阶的自适应滑模混沌通信系统[3]、磁控二氧化钛忆阻混沌系统[4]以及含三个忆阻器的六阶混沌电路[5]等.基于混沌信号的宽频谱、类随机的混沌特性，混沌信号在多种新型混沌通信系统中得到了广泛应用，如基于比例积分反馈控制器的Lü混沌系统的同步实现[6]、低信噪比下混沌扩频数据的快速捕获[7]、独立同分布密钥流混沌通信系统的构建[8]以及基于混沌特性的微电网孤岛的检测[9]等.

然而，由于混沌信号的功率谱分布并不理想，现有的研究成果无法利用混沌信号作为通信载波实现信号的无线传输，这已经成为目前制约混沌信号在无线通信领域应用的一个重要因素.相关研究[10]发现，系统状态变量的相空间运动轨迹与混沌信号功率谱分布具有相关性，因此，可以从状态变量的相空间运动轨迹约束角度来获取具有不同频谱特性的混沌信号.

1 模型的构建和动力学分析

1.1 新混沌系统模型的构建

早在2001年，人们根据Lorenz系统和Chen系统，提出了Lü混沌系统，其非线性微分方程式可以表示为

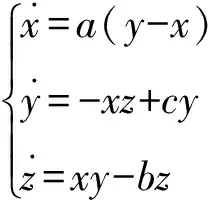
(1)

式中：x、y和z为系统的状态变量；a、b和c为实常数.

当a=36、b=3且c=20时，Lü混沌系统的状态变量相空间轨迹如图1所示.此时状态变量的功率谱如图2所示，其中P为功率谱密度，f为频率.由图1、2可见，Lü混沌系统的吸引子类似于“蝴蝶双翼”，其信号功率谱中0 dB对应的频率约为300 Hz.

在Lü混沌系统的基础上，通过增加一个非线性约束项并调整相应参数来构建新的混沌系统，其非线性微分方程式可以表示为

(2)

当a=2.65、b=100且c=400时，本文对该新系统进行了理论分析.

1.2 基本动力特性分析

1.2.1 对称性和不变性

由于新混沌系统在(x，y，z)→(-x，-y，z)变换下具有不变性，因此，得出新系统的相轨迹是关于z轴对称的，且这种对称不受系统参数a、b和c的影响.

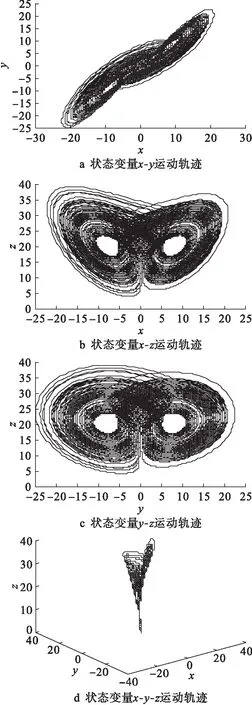
图1 Lü混沌系统的相空间运动轨迹Fig.1 Phase space motion trajectories of Lü chaotic system

图2 Lü混沌系统状态变量的功率谱Fig.2 Power spectrum of state variable of Lü chaotic system

1.2.2 时域图、Poincaré截面图与Lyapunov指数

混沌信号具有非周期性、宽频谱、类噪声等特点.图3为新混沌系统的时域波形图.由图3可见，新系统中的混沌信号同样具有非周期性特点.

图3 新系统的时域波形图Fig.3 Time-domain waveforms of new system

Poincaré截面图可以描述出混沌运动的往复非周期性，如果Poincaré截面既不是有限点集也不是封闭曲线，则对应的系统运动处于混沌运动状态.新系统的Poincaré截面图如图4所示.

图4 新系统的Poincaré截面图Fig.4 Poincaré section diagram of new system

由图4可见，在Poincaré截面处发现一些成片分布且具有分形结构的密集点，因而可以判断该新系统为混沌系统.

Lyapunov指数是定量描述轨线随时间推移相互排斥和相互吸引的特征值，而系统的最大Lyapunov指数是判定混沌系统的重要特征.当系统至少有一个Lyapunov指数大于零时，可以判定该系统为混沌系统.

本文根据Jacobian矩阵并采用四阶Runge-Kutta算法求得新系统的Lyapunov指数，且λL1=75.026，λL2=-7.563，λL3=-123.345.因为新系统中有一个指数为正值，两个为负值，所以该新系统为混沌系统.

维数是非线性系统的一个重要几何特征量，而混沌吸引子具有非整数维数.新系统的Lyapunov维数可以表示为

1+λL1/(-λL2+1)=

1+75.026/(7.563+1)=

9.761 6

(3)

可见，新系统的Lyapunov维数为分数维，从而验证了该系统为混沌系统.

2 运动区域与功率谱分布

混沌信号与周期信号及稳定收敛信号的功率谱分布不同的原因是由于在生成模型中非线性项决定了系统Jacobian矩阵具有不同特征.通过改变非线性项，非线性系统的运动状态可以在不同类型之间进行切换，在频域内表现为混沌信号具有连续功率谱或线状功率谱.为了实现使功率谱密度集中分布在一定频域范围内的目的，利用极限环系统运动轨迹单一且与目标信号相似这一特点，可以在混沌运动状态和极限环运动状态之间找到一个平衡点，使得状态变量限定在一个环状区域内运动，从而在极限环固有频率附近产生新的频谱分量，并最终实现特定频谱范围覆盖.

新系统在Lü混沌系统上增加了非线性约束项ax(x2+y2-b)(x2+y2-c)/(x2+y2).通过实验仿真可以得出参数a影响系统的运动状态，而参数b、c影响系统的运动轨迹在x-y平面投影的内外半径.

当参数b=100、c=400保持不变并改变参数a时，通过仿真可知，当a=0时，系统为Lü系统，且其相空间运动轨迹及状态变量功率谱分别如图1、2所示.

当参数b=100、c=400保持不变且a∈(0，0.3)时，新系统是发散的，其相空间运动轨迹不能收敛于特定区域.

当参数b=100、c=400保持不变且a∈[0.3，2.26]时，新系统的相空间运动轨迹逐渐接近极限环，且随着a值的增大，其最大Lyapunov指数从负值逐渐增大，并逐渐接近于零.当a=2.26时，系统的Lyapunov指数λL1=0.186 4，λL2=-7.235 6且λL3=-290.788 8.当a=2.26时，新系统的相空间运动轨迹与功率谱分别如图5、6所示.

图5 参数a=2.26时新系统的相空间运动轨迹Fig.5 Phase space motion trajectories of new system with a=2.26

图6 参数a=2.26时新系统的功率谱Fig.6 Power spectrum of new system with a=2.26

由图5可见，新系统的相空间运动轨迹在x-y平面的投影接近于正圆.由图6可见，新系统的功率谱分布于固定频率附近，但是由于极限环的形状不理想，因而依然存在谐波分量.

当参数b=100、c=400保持不变且a∈[2.27，2.67]时，新系统逐渐进入混沌状态，此时可以找到极限环运动与混沌运动之间的过渡点.当a=2.45时，新系统的相空间运动轨迹与功率谱分别如图7、8所示.观察图8可以发现，在新系统的固有频率附近逐渐产生新的频谱分量，并呈现出实现目标信号特定频谱覆盖范围的趋势.当a=2.65时，新系统的相空间运动轨迹与功率谱分别如图9、10所示.由图10可见，新系统的功率谱集中分布在一定的频域范围内，但依然存在谐波分量.后期可以通过优化极限环的形状，使得环形轨迹在坐标平面的投影趋近于正圆，从而降低高次谐波所带来的影响.

3 结 论

本文在Lü系统基础上，通过增加非线性约束项并进行参数调节，构建新的三维自治混沌系统，并将该新系统的相空间运动轨迹限定在一定的吸引区域内，从而实现特定频谱范围覆盖.通过以上实验分析可以得出如下结论：

1) 增加非线性项得到的新混沌系统的混沌吸引子的形状与Lü系统的混沌吸引子完全不同.

2) 混沌信号的功率谱与其相空间运动轨迹密切相关，当需要得到特定频谱范围内的混沌信号时，可以通过增加非线性约束项并改变相空间运动轨迹得以实现.

图7 参数a=2.45时新系统的相空间运动轨迹Fig.7 Phase space motion trajectories of new system with a=2.45

图8 参数a=2.45时新系统的功率谱Fig.8 Power spectrum of new system with a=2.45

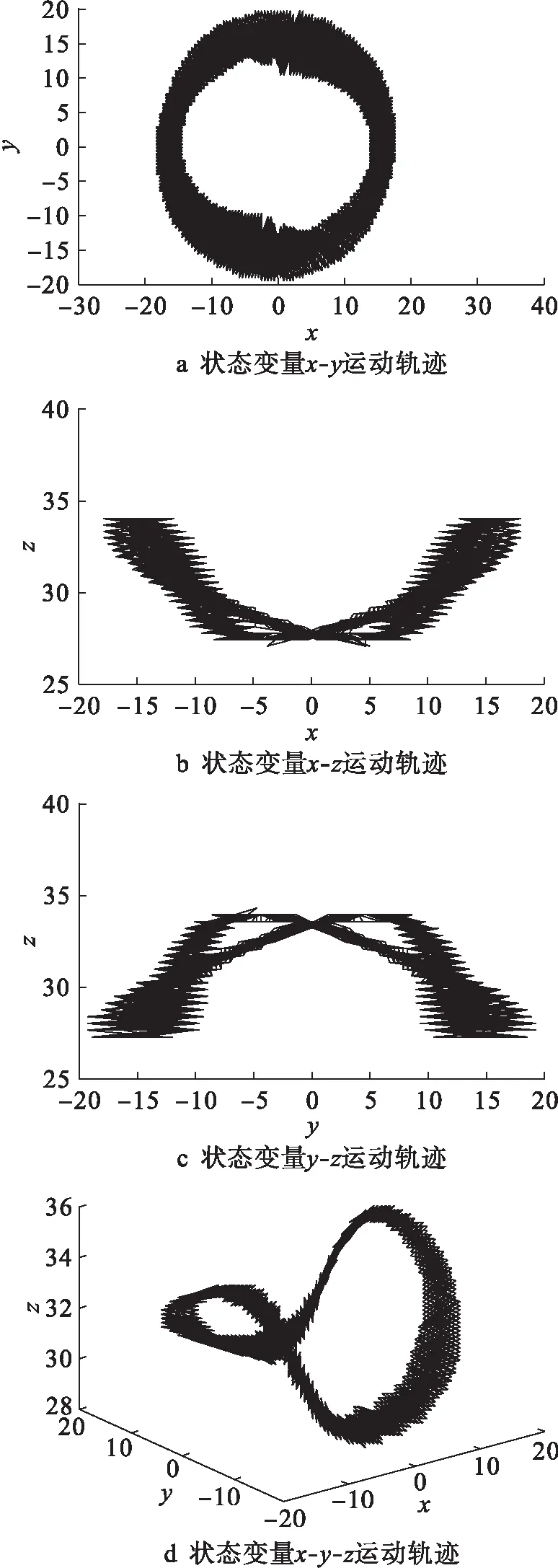
图9 参数a=2.65时新系统的相空间运动轨迹Fig.9 Phase space motion trajectories of new system with a=2.65

图10 参数a=2.65时新系统的功率谱Fig.10 Power spectrum of new system with a=2.65