基于Buck电路的矩阵变换器风机直接转矩控制*

陈 艳，黄灿英，罗小青，万 彬，李升健

(1.南昌大学 科学技术学院，南昌 330029；2.南昌职业学院 工程系，南昌 330004；3.国网江西省电力有限公司 电力科学研究院，南昌 330096)

风电作为一种清洁、可再生的能源[1]，已经从补充能源转变为最具商业前景的能源，风力发电也逐渐成为各国能源发展的方向[2-4].

常用的风力发电系统包括：恒速恒频风力发电系统和变速恒频风力发电系统[5-6].恒频风力发电系统在发电过程中维持风机转速不变，并使用电力变频措施将风机产生的变频电能转化为工频后并入电网，常用于微电网和小规模风力发电系统中[7]；而变速恒频风力发电系统在变速运行时得到恒频的电能，具有提高风能利用率和灵活控制的特点[8].

风力发电机的直接转矩控制是德国和日本学者于20世纪80年代提出的一种电机控制策略[12-14]，其无需将矢量变换到转子坐标系中，而是在定子坐标系中直接实现电机的转速控制[15].直接转矩控制具有计算量小、控制简单、不易受电机参数影响的特点，且具有较高的鲁棒性[16].

1 基于Buck电路的矩阵变换器

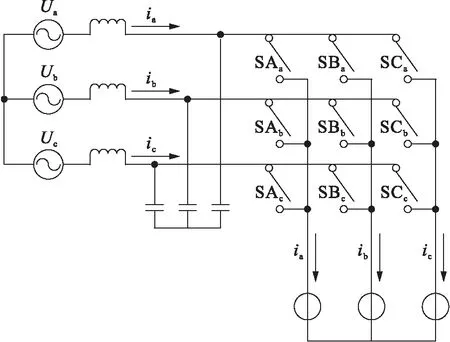
图1 矩阵变换器主电路Fig.1 Main circuit of matrix converter

典型的Buck电路如图2a所示，包括一个负载R、阻抗L、两个普通二极管VD和一个控制通断的IGBT管VT，其中，VD用于阻止反向电压和提供续流通道.图2b为本文改进后的斩波电路，其使用两个背靠背的二极管代替原来的单二极管，并使用两个背靠背的IGBT代替原来的IGBT.改进后的斩波电路使用SPWM方式进行调制控制，并可通过采用适当的控制方法来获得期望频率的电流.如当输入端正弦电流的上半波形时，始终关断VT1和VT4，导通VT3和VD3来续流，导通VD2和VT2来斩波，此时流过负载的电流和加载在负载两端的电压均是正半周期输入；而当输入端正弦电流的下半波形时，始终关断VT2和VT3，而导通VT4和VD4来续流，导通VD1和VT1来斩波，此时流过负载的电流和加载在负载两端的电压均是负半周期输入.

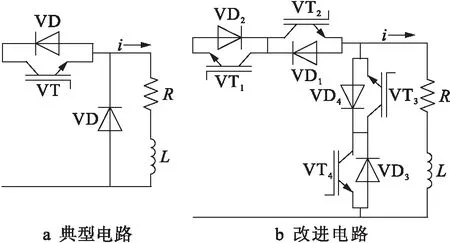
图2 Buck电路及改进单相电路Fig.2 Buck circuit and improved single-phase circuit

由于SPWM自身的缺陷，使得输出波形极不稳定，易受输入电压波动的影响.当输入存在谐波电压时，输入的三相对称电压脉动将错误地导通或关断IGBT，从而产生大量的输出谐波.因此，本文使用电流滞环控制的方式来避免谐波污染，并根据期望输出电流的相位来相应地导通或关断IGBT管.

将图2b的输入端从单向扩展为三相，可以得到图3所示的三相输入矩阵变换器.图3a为单向输出矩阵变换器，每一相的导通和关断方式与单向输入单向输出时的电路类似.若去掉图3a的续流回路且采用双极性控制策略，可以得到图3b所示的电路结构.电路控制策略为：假设期望输出为正半周期电流，并比较三相电压值的大小，将导通电压值最高线路对应的IGBT管进行斩波，将导通电压值最低的线路对应的IGBT管进行续流.简化图3b结构可得到图3c所示的矩阵变换器，其使用双向可控开关管SAa、SAb和SAc来控制线路的导通与关断，从而得到期望输出频率的交流电.由于实际中使用的是感性负载，因此，这种矩阵式变换器在工作时必须同时对电压最高的一相进行斩波，并将电压值最低的一相进行续流.

图3 单相三相矩阵变换器Fig.3 Single phase-three phase matrix converter

2 变换器的风机直接转矩控制

2.1 风机发电系统结构

本文主要研究应用于微电网分布式电源中的永磁直驱风力发电机的直接转矩控制策略.永磁直驱风力发电机减少了励磁装置和励磁线圈，主要采用永磁材料制造.相比于双馈异步风力发电机，其具有损耗小、能量转换效率高、结构简单和可靠性强的特点.

永磁直驱风力发电机的直接转矩控制系统结构图如图4所示.该系统主要由风机、并网通断电开关装置、永磁同步发电机(PMSG)和基于Buck电路的矩阵式变换器构成，并使用定子滤波器过滤输入矩阵式变换器的谐波，且使用网侧滤波器过滤矩阵式变换器开关动作产生的输出谐波.永磁同步发电机的转子侧采用永磁电极，在定子侧使用对称三相绕组来直接控制风机发电.该控制系统通过矩阵式变换器将风机产生的不同频率和幅值电压转化为符合电网实际需求的恒定幅值与频率的交流电来实现并网.

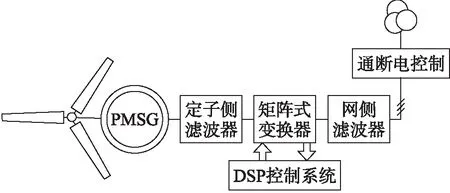
图4 永磁直驱风力发电机的直接转矩控制系统结构图Fig.4 Structure diagram of direct torque control system of permanent magnet direct driving wind turbine

2.2 PMSG和矩阵式变换器的数学模型

为了使电压满足并网的条件，需要有效控制输出电压矢量，以控制发电机能量的单向流动，因此，本文首先研究了PMSG和矩阵式变换器的数学模型.

2.2.1 PMSG数学模型

当PMSG运行在静止坐标系时，假设发电机的转动惯量为J，则有PMSG数学模型为

(1)

(2)

Ψs=Lis+ΨPMeJθ

(3)

(4)

式中：T、Te分别为输出转矩与电磁转矩；Ψs、ΨPM分别为定子磁链与转子磁链幅值；Rs为定子电阻；is、uc分别为定子电流与电压值；L为定子感抗；θ为转子磁链相位；w为风机转速；np为转子极数.

2.2.2 矩阵式控制器数学模型

在建立数学模型时需要考虑电网谐波对矩阵式变换器的影响，因此使用代数方程和微分方程相结合的方式来表示其数学模型，即

(5)

(6)

(7)

式中：dr、di分别为逆变级调制值与整流级调制值；i、is分别为电网的电流值与定子电流值；Cs为定子电容；uc、udc分别为定子电压及直流平均电压；idc为直流平均电流.

2.2.3 网侧数学模型

永磁直驱风力发电机的直接转矩控制系统在电网侧添加了滤波电路，并直接与电网相连，则可构建电网侧数学模型为

(8)

式中：Lg为输出端滤波器的电感；ug为电网的电压.

当转子位于旋转坐标系时，在d-q坐标系中分解式(1)～(8)所示方程，则有

(9)

式中，各变量的定义如图5等效电路图所示.

2.3 控制策略

分析整个系统模型可知，为了使输出电压满足并网恒频的要求，必须完全控制PMSG转子的转速.在2.2节的数学模型中，逆变级调制矢量dr和整流级调制矢量di可得到较好地控制，并可以通过控制这两个自由度来控制整个系统.为了简化控制，本文假设矩阵式变换器的电压矢量与电流矢量同相位，则di取一定值，并有

(10)

式(10)所示的假设，不仅能降低控制成本，减小控制的难度，还能提高电压的传输比.

本文使用反馈线性化法来设计非线性控制器，通过坐标变换将非线性系统转化为线性系统，并使用线性控制理论来控制，控制方程表达式为

(11)

(12)

(13)

式中：上标r为转子变量；上标s为定子变量.为了最大限度地吸收风能，需要使风机的转速和风速同步变化，使用式(12)得到的转速为w，期望转速为w*，则同步电机PMSG的速度误差为e=w-w*.

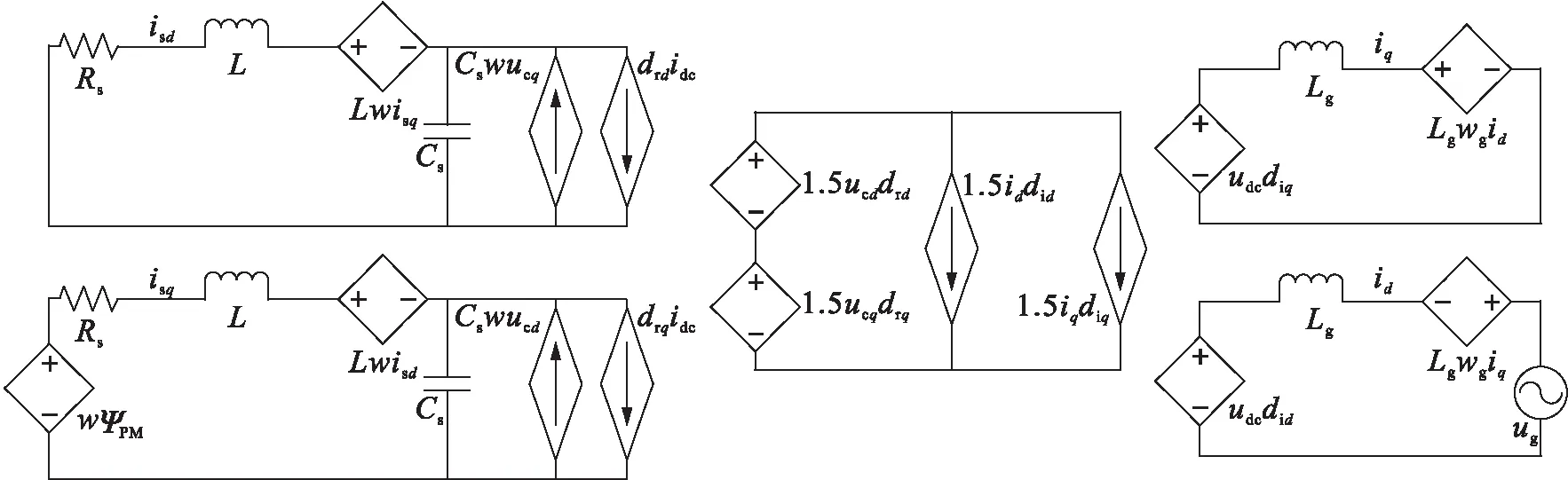
图5 d-q坐标系等效电路图Fig.5 Equivalent circuit diagram of d-q coordinate system

3 仿真分析

本文使用Matlab软件中的Simulink工具箱搭建仿真模型，并以1.5 MW永磁直驱风力发电机作为研究对象，仿真系统整体结构如图6所示.

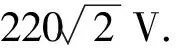
由图7可以看出，电磁转矩脉动比较剧烈，但系统整体的动态响应特性优秀，尤其是在第50 s时，风速发生跳变，电磁转矩能随之变化，从而表明，本文设计的矩阵式变换器能提高系统的动态响应性能.

4 结 论

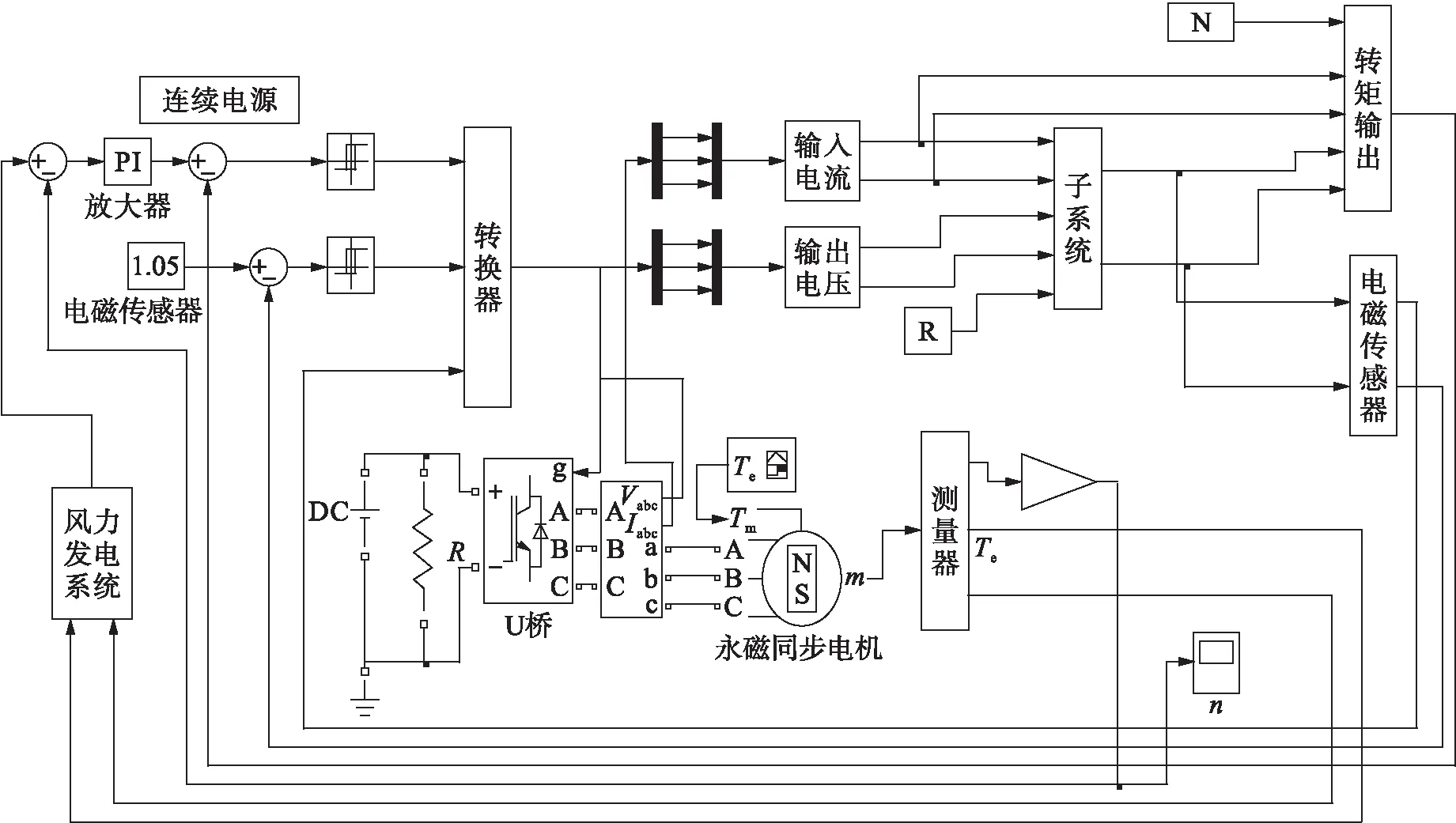
图6 仿真系统结构图Fig.6 Structure diagram of simulation system

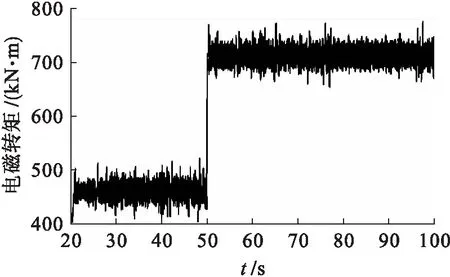
图7 电磁转矩随时间的变化结果Fig.7 Change results of electromagnetic torque with time

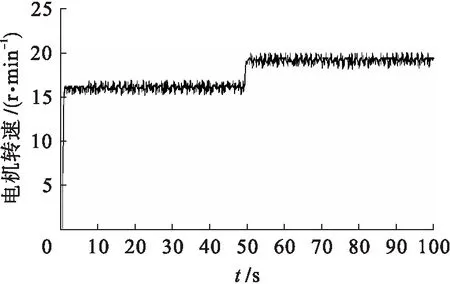
图8 电机转速随时间的变化结果Fig.8 Change results of motor speed with time