料仓中湿颗粒的卸料流型

，, , ，

(1.南京工程学院能源与动力工程学院，江苏南京211167; 2. 东南大学能源热转换及其过程测控教育部重点实验室, 江苏南京210096)

料仓是工业生产中散体贮存的重要设施，料仓卸料是典型的散体流动问题。广义上来讲，料仓卸料主要有2种类型，即中心流(funnel flow)与整体流(mass flow)[1-2]。整体流是指卸料时所有散体都处于运动状态，并贴着垂直部分的仓壁和收缩的料斗壁滑移，散料的流动通道与料仓壁是一致的。中心流动是指卸料时散体沿着卸料口上端的管状通道往下流动的流动形式，即随着管内散体的流出，散体上表面在下降，上部散体不断流入管状通道内流向仓外，形成了先进的可能后出的流动效应。

工业生产中出现的很多流动问题，像架桥、鼠洞、喷流、离析、振动、磨蚀等都是与中心流有关[3]，即当料仓为整体流料仓时，上述大多数问题都可以避免，因此，对料仓物料的流动模式(卸料流型)的研究就具有重要的指导意义。

关于料仓流型的研究，大多集中在料仓结构、物料特性和操作条件[1-2,4-5]对卸料流型的影响上。其中，以Jenike的研究[1-2]最为著名，其应用连续介质模型发展了一系列通过了试验验证的料仓设计理论，取得了广泛的应用。

图1即为楔形料仓以及给定物料内摩擦角下的Jenike设计图之一。

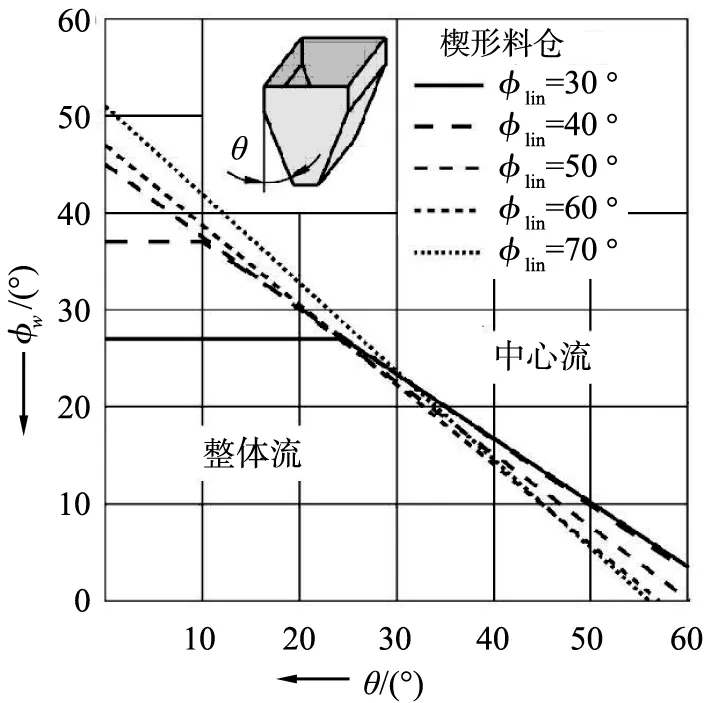
图1 Jenike楔形料仓设计图Fig.1 Jenike’s design chart of wedge hopper

根据Jenike的理论方法，物料的内摩擦角、壁摩擦角以及料仓的几何参数，如料仓的半顶角、出口尺寸、形状等，共同作用决定物料在料仓中的卸料模式。

Ketterhagen等[6]采用离散单元法系统研究了干颗粒从圆柱形料仓以及楔形料仓中的卸料流型，旨在从颗粒尺度研究颗粒特性、料仓结构对卸料流型的影响规律。刘杰[7]用实验方法分析了9种物料在料仓中的重力卸料流型，重点研究了粒径和料仓半顶角对卸料流型的影响规律，半顶角越小，粒径越大，越容易获得整体流。陶贺等[8]研究了椭球形干颗粒在移动床内的流动特性，采用离散元法分析了椭球干颗粒物性对卸料流型的影响规律。

由于湿颗粒之间有间隙液体的存在，因此其在料仓中的卸料特性与干颗粒也有着显著的差异，然而对湿颗粒卸料流型的详细研究未见报道。

本文中采用离散单元法，对湿颗粒在楔形料仓的卸料流型进行系统研究，从微观尺度分析湿颗粒颗粒特性以及料仓结构对卸料流型的影响规律，并将结果与Jenike理论进行对比，分析2种方法的符合程度，旨在从数值模拟的角度揭示湿颗粒在料仓中的流动模式问题，以期为料仓的设计运行提供一定的参考。

1 基于离散单元法的湿颗粒数学模型的构建

1.1 颗粒作用模型

1)法向接触力

2013年，海委通过岳城、潘大水库及漳河上游河道向天津、河北、河南等地安全供水13亿m3，河北四库向北京应急调水达4.3亿m3。实施山西、河北向北京市集中输水，调水7000万m3。实施引黄济冀，通过位山线路将向河北调水2.8亿m3。积极编制南水北调东中线工程补充规划，加快完善流域城乡供水河网体系。

当2个颗粒发生碰撞时，法向接触力采用Walton[9]和Braun[10]提出的部分闭锁、迟滞弹簧双线性接触模型计算，则Fnij可以表示为

(1)

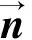
2)切向接触力

2个颗粒间切向接触力Ftij可以表示为

(2)

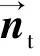
3)滚动摩擦力矩

为了把颗粒非球形度或是颗粒表面的粗糙纹理对颗粒运动的影响考虑进去，滚动摩擦以力矩形式表示

MR,ij=-μR|Fnij|ω/|ωi|

(3)

式中：μR为滚动摩擦系数；ωi为角速度。

1.2 液桥作用模型

1)液桥力

考虑摆动状态连接方式时湿颗粒间作用力，2个不等直径球间的液桥力计算式[11-12]为

(4)

(5)

，

(6)

(7)

式中：ri、rj分别为2个颗粒的半径；γ为液体表面张力；α为接触角；h为颗粒间距；V为液桥的体积；A、B、C为无因次回归系数。

2)黏滞力

由填隙液体的黏性引起的黏滞力采用Adams和Perchard[13]通过润滑理论获得的2个颗粒间摆动液桥法向黏滞力的解析解，

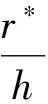
(8)

(9)

式中：η为液体的黏度；vn为颗粒间的相对速度；r*为等效颗粒半径。

3)极限液桥距离

只有当颗粒间距小于某个数值时，液桥才是稳定的，此时液桥长度称为液桥极限分离距离hrup。Lian等[14]提出了2个球之间液桥稳定性的判定标准：对于非黏性液体，当接触角小于40 °的时候，极限分离距离hrup与液桥体积V的立方根成比例，

hrup=(1+0.5α)V1/3。

(10)

4)颗粒Bond数(Bo)与无因次含液量V*

为了表征湿颗粒系统相对内聚力的大小，Nase等[15]提出了一个重要参数，颗粒Bo，定义为最大黏着力与颗粒重力之比

(11)

另外一个重要参数为无因次含液量V*[16]，定义为液桥的体积与球颗粒半径立方之比，表征湿颗粒系统中含液量的多少。

(12)

1.3 颗粒运动方程

对于湿颗粒，系统内任意一颗粒i与周围其他颗粒(ki个颗粒)或边界发生接触，根据前述接触模型计算颗粒i所受到的合力和合力矩，其平动和转动控制方程，表示为

(13)

(14)

式中：mi为颗粒i的质量；G为颗粒的重力；Ii为颗粒i的转动惯量;t为时间。

2 数值计算条件

表1为模型的计算条件和参数。 计算颗粒为单分散且颗粒直径服从正态分布的玻璃珠，颗粒平均直径dp为0.002 m，密度为2 500 kg/m3，颗粒为湿颗粒。 模拟的对象为三维楔形料仓，料仓高H为0.16 m, 料仓出口宽度W0/dp=10，料仓宽度W/W0=5，料仓半顶角为θ为30 °。

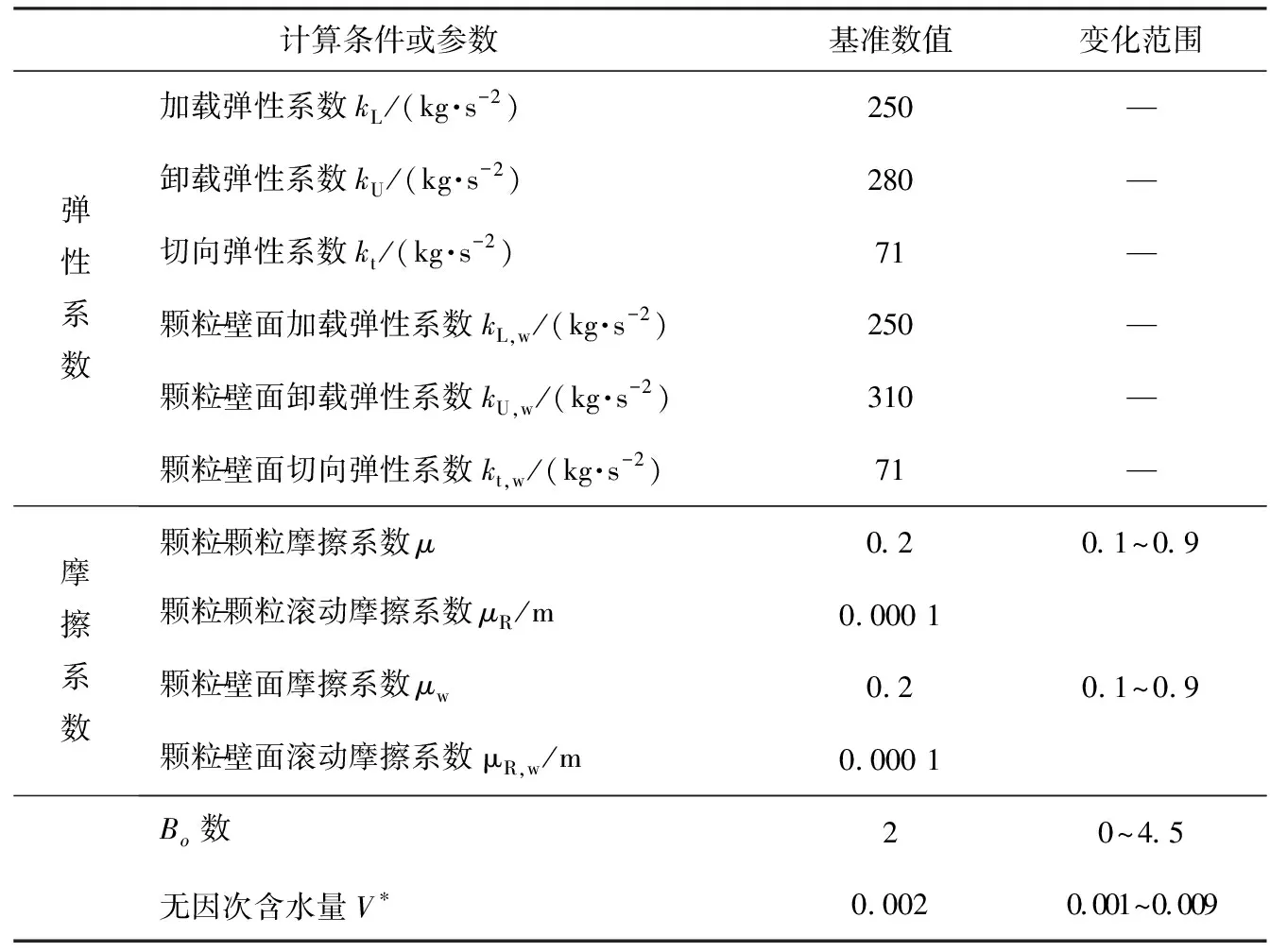
表1 模型的计算条件和参数

为了定量分析料仓流型，采用流型量化指标(mass flow index，MFI)作为判别标准[6]，定义为壁面附近颗粒的平均速度与料仓中心线处颗粒的平均速度之比，其值用AMFI表示。图2表示壁面处和中心线处的计算区域，即边壁处计算区域为1个颗粒直径宽度，而中心处为2个颗粒直径宽度。根据Johanson等[17]的研究可知，AMFI=0.3是整体流与中心流的分界线，AMFI>0.3表示卸料为整体流，AMFI<0.3为中心流。

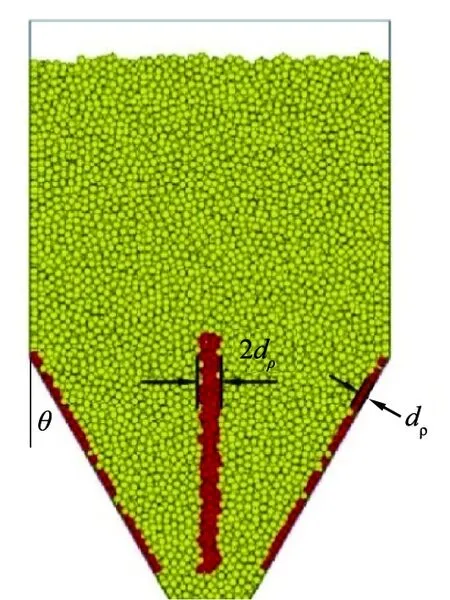
图2 平均速度计算区域Fig.2 Mean velocity calculation area

3 模拟计算结果及分析

3.1 不同物性颗粒的流型

为了定量研究不同物性参数的颗粒在卸料过程中的流型，保持料仓出口尺寸、 料仓半顶角、 宽度等几何因素以及颗粒直径不变，分析湿颗粒-壁面滑动摩擦系数和湿颗粒-颗粒滑动摩擦系数对AMFI的作用。

图3为湿颗粒-壁面滑动摩擦系数对AMFI的影响图。从图中可以看出，湿颗粒壁面摩擦系数对流型有很大的影响，随着湿颗粒-壁面滑动摩擦系数的增加，其AMFI显著降低，后随壁面摩擦系数的增加，下降幅度不大。料仓流型也由整体流逐渐转变为中心流，发生转变的壁面摩擦系数为0.31，随壁面摩擦系数的继续增大，保持中心流流型不变。这是由于湿颗粒壁面之间的滑动摩擦系数增大，以及湿颗粒壁面之间的液桥黏性力，使得壁面附近的湿颗粒流动阻力变大，致使壁面处湿颗粒向卸料口的运动速度减小，而中心处颗粒则顺利地以团聚形式在重力作用下向出口流动，致使边壁处湿颗粒速度和中心处速度相差较大，因此，其AMFI值比较小。

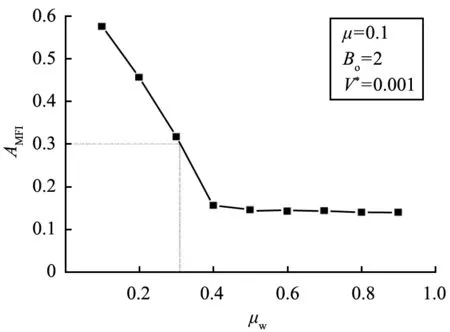
图3 湿颗粒-壁面摩擦系数对AMFI的影响Fig.3 Effect of wet particle-wall friction coefficient on AMFI

图4为湿颗粒-颗粒滑动摩擦系数对AMFI的影响图。从图中可知，与湿颗粒壁面滑动摩擦系数相比，湿颗粒-颗粒滑动摩擦系数对流型的影响并不显著，随湿颗粒-颗粒滑动摩擦系数的增加，其AMFI值变化不大，且其流型一直保持为整体流。由此可见，与湿颗粒壁面摩擦系数相比，在控制料仓卸料流型的物性因素中，壁面摩擦系数占主导地位。

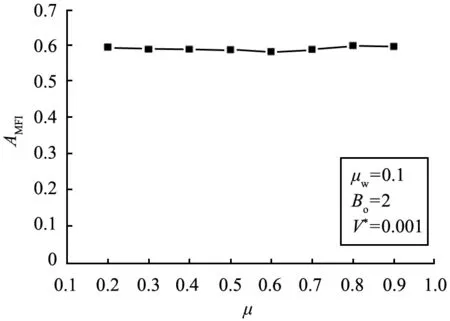
图4 湿颗粒-颗粒摩擦系数对AMFI的影响Fig.4 Effect of wet particle-particle friction coefficient on AMFI

3.2 不同料仓几何尺寸的流型

为了将模拟结果与图1的Jenike设计图表进行对比以验证模拟的正确性，采用文献[6,18-19]所建立起来的微观摩擦与宏观摩擦之间的联系来选取模拟中所要用到的微观摩擦系数。表2总结了模拟中所用到的微观参数以及相应的宏观参数。

图5为模拟所得的不同半顶角以及壁面摩擦角时的卸料流型并与Jenike设计图表对比的三维图。其中，分布在黄色平面上的蓝色线代表Jenike提出的中心流与整体流分界线，图中为内摩擦角15 °的分界线。由图可知，半顶角不变时，其AMFI数值都是随着湿颗粒壁面摩擦角的增大而减小。壁面摩擦角恒定时，半顶角越小，其AMFI值越大。这是因为，湿颗粒由料仓的垂直部分流动到收缩段时，颗粒每下降一个微小的高度，都要重新排列，颗粒的原有层面呈不均匀下降，以适应截面收缩的变化。料仓半顶角越大，颗粒越接近出口，颗粒间的挤压现象越明显，边壁处的颗粒速度较慢，中心处颗粒速度较大，其AMFI越小。半顶角越大，边壁与中心处的速度差越大，AMFI也越小。此外，模拟所得的三维图显示的总体趋势是比较大的AMFI分布于黄色平面左上角，比较小的AMFI则位于右下角，这与Jenike理论预测结果类似，见图1所示。但是，模拟所得的整体流与中心流的分界线与Jenike所提出的分界线有所不同。Jenike理论所预测的整体流与中心流分界线由2条斜率不同的直线分段表示。相反，模拟预测所得分界线是一连续曲线，Jenike预测的整体流的范围是朝着黄色平面左上角一较小的范围，因此，对整体流和中心流转变预测比较保守，而模拟预测范围则较大。

表2 模拟计算中所用到的参数汇总

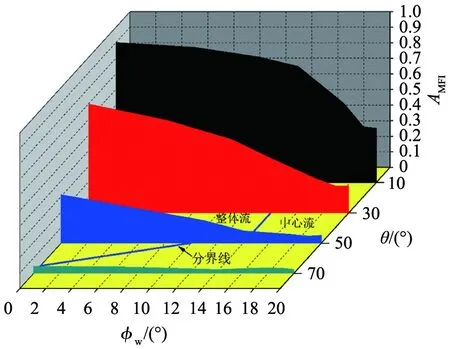
图5 半顶角对AMFI的影响并与Jenike设计图表对比情况Fig.5 Effect of hopper half angle on AMFI and comparison with Jenike design chart

3.3 不同料仓几何尺寸的流型

图6表示了相同物性的颗粒在半顶角相同、卸料口开口尺寸不同的料仓中卸料时AMFI变化情况。由图可以看出，随着卸料口尺寸的减小，其AMFI是减小的，但减幅不大，且流型仍为整体流。

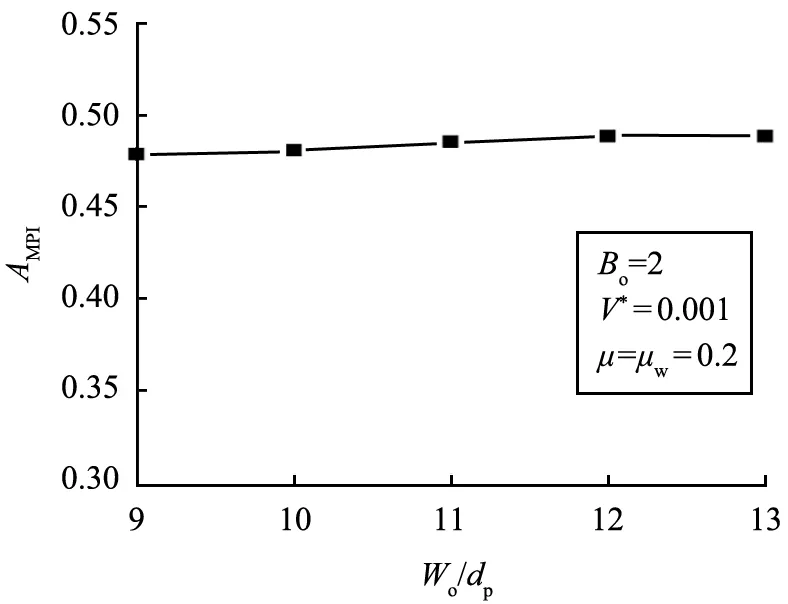
图6 卸料口开口尺寸对AMFI的影响Fig.6 Effect of hopper outlet size on AMFI

3.4 Bo数对卸料流型的影响

图7表示Bo数对料仓卸料流型AMFI变化情况的影响。由图可以看出，在料仓结构尺寸不变，湿颗粒物性不变的情况下，随着Bo数增大，其AMFI略有减小后增大，但整体变化幅度不大，且流型仍为整体流。

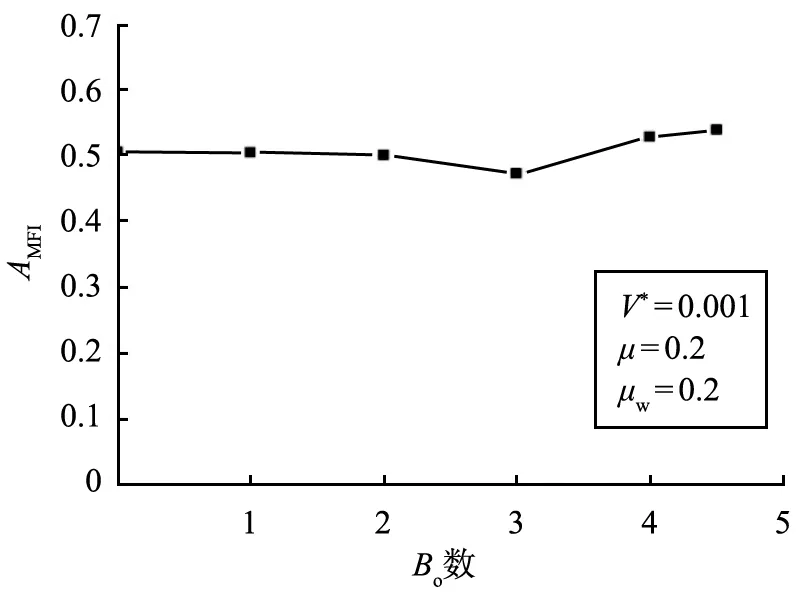
图7 Bo数对AMFI的影响Fig.7 Effect of Bo number on AMFI

3.5 对卸料流型的影响

图8为无因次含液量对AMFI变化情况的影响图。由图可以看出，在料仓结构尺寸不变，颗粒物性不变的情况下，改变无因次含水量，其AMFI值变化不大，且流型仍为整体流。这是因为虽然含水量增加，但其湿颗粒-颗粒摩擦系数、颗粒壁面摩擦系数不变，表现在宏观参数上，其内摩擦角和壁摩擦角都不变，所以，在保持料仓结构、颗粒物性不变的情况下，含水量增加，对AMFI值的影响很小。

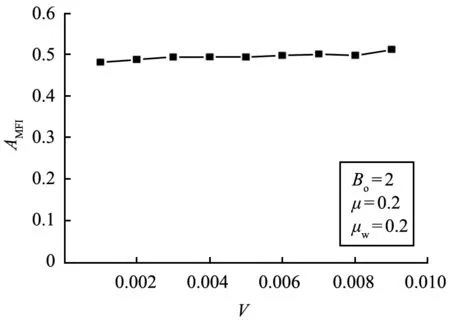
图8 无因次含液量对AMFI的影响Fig.8 Effect of dimensionless liquid content on AMFI

4 结论

本文中建立了湿颗粒离散元模型并研究了料仓卸料流型与湿颗粒摩擦特性、料仓半顶角、料仓开口尺寸以及仓壁摩擦特性之间的相互关系，并与Jenike理论预测结果进行对比，获得如下结论：

1)料仓AMFI随湿颗粒-颗粒滑动摩擦系数、湿颗粒-壁面摩擦系数的增大而减小，随湿颗粒-颗粒摩擦系数的增加减小幅度不大，但随湿颗粒-壁面摩擦系数的增大而显著减小，且流型由整体流转变为中心流。与湿颗粒摩擦系数相比，壁面摩擦系数对流型的影响占主要地位。

2) 与壁面摩擦系数对AMFI的影响相似，随着料仓半顶角的增大，流型将由整体流转变为中心流，且对料仓卸料流型量化预测结果与Jenike理论预测结果一致。卸料口开口尺寸对AMFI值影响不大。

3) 在保持湿颗粒物性和料仓结构不变的情况下，改变Bo数和无因次含水量对AMFI值影响不大。