对合情推理的思与行

严彪

[摘要]学生推理能力的发展应贯穿于整个数学学习过程。由两次“加法运算律”的对比教学得出，引导学生进行合情推理，培养学生思必有源、推必有理、言必有据的思维品质，才能真正落实学生数学核心素养的培养目标。

[关键词]加法运算律;合情推理;类比推理;归纳推理

[中图分类号]

G623.5

[文献标识码]A

[文章编号] 1007-9068（ 2019）35-0067-02

推理是由一个或几个已知判断（前提）推出新判断（结论）。推理在数学中则更纯粹、更直接，也更彻底，它是数学基本的，也是主要的思维方式，从这一角度来看，数学教学活动的过程可以视作数学推理教學的过程。

关于推理，依据不同的分类标准，其分类结果也各不相同。课程标准指出：推理一般包括合情推理和演绎推理。小学阶段是学生推理能力发展与形成的重要时期，针对小学生的思维特征和数学知识的特点，小学数学中的推理及其教学具有一定的特殊性。

合情推理是从已有的事实出发，凭借经验和直觉，通过归纳和类比等推断某些结果。它是一种合乎情理的推理，常与感知、迁移、联想和想象等心理活动相伴，其过程也体现思维的跳跃性和结论的或然性。因此，它不但是启动和推进思维的小船，还能帮助学生发现事物的规律，给学生提供研究的线索和思路，从而猜想和发现结论。

【教学片段】加法交换律

第一次教学

师：28个男生跳绳，17个女生跳绳，跳绳的有多少人？解决这个问题时你是怎样想的？

生1：把男、女生人数合起来，就是跳绳总人数。

师：能用数量关系式来表示解题思路吗？

生2：男生跳绳人数+女生跳绳人数=跳绳总人数。

生3：女生跳绳人数+男生跳绳人数=跳绳总人数。

生4：男生跳绳人数+女生跳绳人数=女生跳绳人数+男生跳绳人数。

师：能列式计算吗？

生5：28+17=45。

生6：17+28=45，即28+17=17+28。

师：你能再写几个这样的等式吗？（类比推理）

（学生汇报;教师评价学生写出的等式）

第二次教学

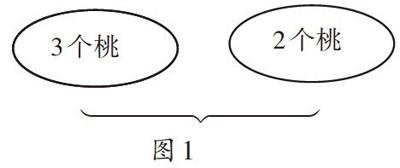
师：还记得我们很小的时候是怎样做加法的吗？（如图1）两盘一共有多少个桃？

师：要求一共有多少个桃，我们常常是这样数的。从左往右数，得到3+2=5;也可以倒过来数，得到2+3=5。你从中发现了什么？

生1：3+2=2+3。

师：明明是交换加数的位置，为什么结果都不变呢？

生2：无论先数哪一堆，桃子总量保持不变。

师：（如图2）改变数的先后顺序，桃子的总量会不会变化呢？

生3：这回不用数，可以列式计算。28+17=45。

生4：17+28=45，即28+17=17+28。

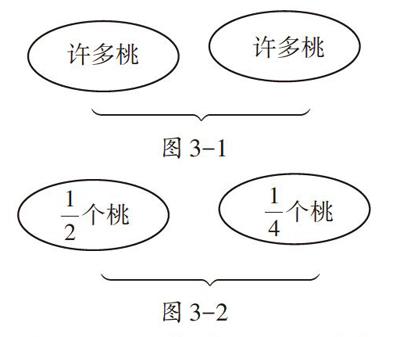
师：（如图3-1）如果桃子的数量再增加，多到数也数不清;（如图3-2）或者是桃子的数量减少，少到只剩下零零碎碎的部分，还是求一共有多少个桃。数的顺序改变，桃子的总量会改变吗？

师：我们得出的几道算式中，交换加数的位置后和不变。像这样的情况，还能举出别的例子吗？

生5：3+2=2+3。

生6：28+17=17+28。

生7：1/2+1/4=1/4+1/2。

师：观察、比较这些等式，你有什么发现？

生8：两数相加，交换加数的位置，和不变。

师：为了表示这无穷多的情况，可以用字母来表示。用a+b表示任意两个数相加，交换加数的位置就变成了b+a，结果不变。这条加法运算律就可以写成a+b=b+a，它就叫作“加法交换律”。

【评析：类比推理简称类推、类比，是从特殊到特殊的推理。它是两个或两类对象在某些属性相同或相似的前提下，通过比较而推断出它们在其他属性上也相同或相似的结论。上述的两次教学都是在同类对象之间进行推理的，学生“再写几道这样的等式”，都是以对象所具有的“两数相加，交换位置”的共同属性为前提，推出它们具有相同属性，即“和不变”的结论。其中，第一次教学中的类比推理显得层次单一，而第二次教学中的类比推理则从有限到无限，从整数到非整数，在都具有“两数相加，交换位置”的共同属性的前提下，推出它们都具有“和不变”的共同属性。通过这样层层递进、螺旋上升的思维训练，学生自然而然地学会用推理去分析和解决问题。

类比推理在思维方面是横向的，虽然推出的结论可能是或然的，但它有提供思路，进而引出猜想、发现结论的效用。在教学活动中，学生常常需要联系新旧知识的某些相同或相似之处进行类比迁移、自主探索。如苏教版教材五年级下册转化策略中的要求“1/2+1/4+1/8+1/16”

的结果，就可以运用数形结合的数学思想，将其转化为“把正方形看作单位‘1，求其中的涂色部分”来解决;求“15+16+17+18+19+20+21+22+23+24”这几个连续自然数的和时，运用迁移的规律，将求“几个连续自然数的和”转化为求“上底15、下底24、高10的梯形的面积”。以上类比推理，都是在两类不同对象具有“数列中各数之间有一定的规律”这一相似属性的前提下，推出它们又都具有相同属性——可以转化成相应的图形面积的结论。】

【教学片段】加法结合律

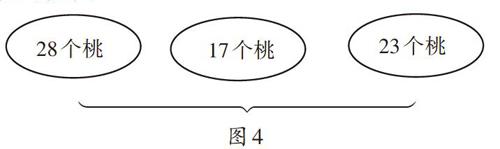
师：之前是增加每堆桃的个数，如果增加桃子的堆数呢（如图4）？

生1：28+17+23=68。

生2：17+28+23=68。

生3：28+（17+23）=68。

生4：17+23+28=68。

师：对于28+17+23=68和17+28+23=68，你有什么想法？

生5：结果相同，位置改变，说明加法交换律也适用于三个数相加。

师：对于28+（17+23）=68和17+28+23=68，你有什么想法？这样两个算式什么相同，什么又不同了呢？是什么变化了呢？

生6：多了小括號，顺序就变了。先数前两堆，或先数后两堆，并不改变桃子的总量。

生7：不需要再计算，桃子的总量肯定不会变化，因为桃子的总数不会因为数的先后顺序而发生变化。

生8：也就是说，像（28+17）+23=28+（17+23）这样的算式，我们还可以写出很多很多。

生9：如果用a+b+c来表示任意的三个数相加，那么改变运算的顺序，结果不变。可以表示为（a+b）+c=a+（b+c），这个规律就叫作“加法结合律”。

师：加法交换律和加法结合律，统称为“加法运算律”。

【评析：归纳是通过对某类事物中的若干特殊情形的分析得出一般结论的思维方法，归纳推理则是由特殊到一般的推理，是以个别对象的属性为前提，推出此类对象一般属性的结论。归纳推理都是以各自之前的每一个类比推理中具有特殊或个性属性的结论为前提，得出具有一般和共性属性的结论，即“两数相加，交换加数的位置，和不变”与“三个数相加，改变运算的顺序，和不变”。而“加法运算律”也是对“加法交换律”和“加法结合律”的归纳概括。归纳推理又可以分为完全归纳推理和不完全归纳推理。】

【总评】

1.自主推理，替代被动接受

小学数学中有许多定理和规则。对于规则的教学，可以直陈其然，但对小学生来说，这是一种简单的、被动的接受性学习。要有利于学生的认知和思维的发展，就应赋规则教学以理性思考。教师应积极寻找和发掘教材中适合学生推理的内容，善于引导学生从对象的现象到本质进行思考和推理，或由因导果，或执果索因，并有意识地培养学生思必有源、推必有理、言必有据的思维品质，使学生“在游泳中学会游泳”，在运用和思辨中发展能力，在感悟和积累中逐步形成关于推理的数学核心素养。

2.借助推理，培养创新意识

推理的过程常常伴随着联想和迁移等心理活动。开展推理活动，尤其是合情推理活动，也利于培养学生的创新意识。让学生在推理活动中凭借直觉、运用迁移、展开联想、发挥想象，乃至突发灵感、达成顿悟，得出创新性的结论或观点。虽然这些结论或观点可能是粗糙的，但经过一定的加工和完善，也许就成了学生学习中和思维上的金点子。

（责编金铃）