局部冲刷坑发展过程的泥沙输运特性
齐梅兰,石粕辰
(1.北京交通大学 土木建筑工程学院,北京 100044;2.北京交通大学 结构风工程与城市风环境北京市重点实验室,北京 100044)
1 研究背景
水下结构物的局部冲刷问题,具有水流结构及泥沙输运随三维空间和时间尺度变化的复杂性,数值模拟研究受到广泛关注[1-3],以期深入了解冲刷机理并获得准确的冲刷预测。根据物理机制,描述局部冲刷的数学方程包括水流运动、泥沙运动和床面变形方程,其中泥沙运动状态很复杂,包括泥沙临界起动条件以及推移质运动、悬移质运动模式识别等,如考虑不周则可能影响局部冲刷的数值模拟结果。
天然河流紊流方程瞬态数值解的直接模拟甚至大涡模拟因需占用大量的计算资源[4-5],工程中多用雷诺平均(RANS)方程的数值模拟。非恒定的雷诺平均方程(URANS)改进了恒定的RANS方程在捕捉复杂涡流能力方面的缺陷,提高了计算精度[6-7]。RANS方程中的紊流脉动项多作线性涡黏应力模型处理,针对涡黏系数又派生了包括k-ε在内的多种模型。其中,标准k-ε模型对近壁区和逆压梯度区流动的模拟存在不足,重整化群RNGk-ε模型考虑了黏性涡的尺度,在模拟涡流特性方面有一定优势[8-9]。
受水流作用,床面泥沙可呈推移、悬移或二者兼之的运动状态。在局部冲刷的数值模拟中,Olsen等[10]仅考虑了悬移质输运,更多的学者则只考虑推移质输运[11-14],也有考虑推移质和悬移质即全沙输运的[15-17]。墩柱局部冲刷分为清水冲刷和动床冲刷两种条件(分别表示床沙未起动和起动的均匀来流条件),Burkow等[12]对清水冲刷条件采用了推移质泥沙运输;而DIXEN等和JIA等在动床条件下也仅考虑了推移质,但引入了柱前涡流[13]或脉动流速[14]对水流时均切应力做了增强性的修正;Alemi等[18]即使对于清水冲刷也采用了全沙输运模型;Baykal[15]根据其计算则认为如不考虑悬移质输运,墩前最大冲刷深度减小50%,无论是否进行涡流及脉动修正;Roulund等[11]在其计算条件下认为悬移质不重要;Radice等[19]的试验尽管是动床冲刷,也称冲刷过程中悬移质输运不重要。可见目前局部冲刷模拟中,对泥沙输运物理模式的合理选用未取得共识,作者认为,这一问题需要通过深入探讨推移质和悬移质输运在局部冲刷中的贡献加以解决。
本文基于水、沙、床面变形相互作用的物理机制,采用瞬态的URANS方程并辅以RNGk-ε湍流模型封闭方程组、推移质和悬移质输沙模型以及床面质量守恒方程,分别在清水冲刷和动床冲刷条件下,对水流、泥沙运动及床面变形三者之间的循环作用求解,模拟了墩柱冲刷过程。通过追踪冲刷过程中墩周的紊流特性、悬移质和推移质输沙率的变化,分析悬移质和推移质输运对局部冲刷发展的贡献及其与紊流特性的相关趋势,以期阐明局部冲刷泥沙输运模式的选用条件。
2 数值模型
水流运动由不可压缩流体的连续方程和雷诺时均紊流方程(URANS)控制:
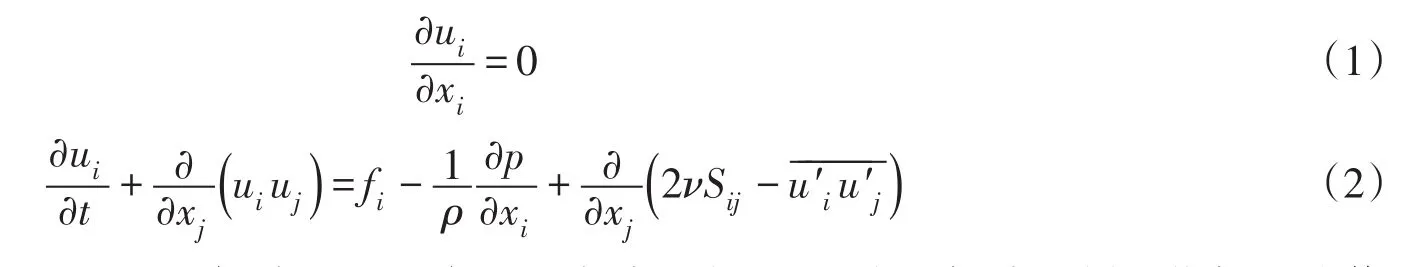
式中:xi和ui分别为直角坐标系下的坐标分量和对应的速度分量(i,j,k为坐标分量循环指标,取值1,2,3,分别表示x,y,z方向);t为时间;n为水的运动黏度;p为水的平均压强;fi为流体单位质量力为雷诺应力;Sij为平均应变率张量:

2.1 紊流模型式(2)中紊流的雷诺应力项采用湍流涡黏模型,其本构关系为:

式中:δij为克罗内克符号;为紊动能;νt为紊动涡黏系数。

式中:k为紊动能;ε为紊动能耗散;Cμ为常数,通常取值0.09。为了能够准确捕捉桥墩周围的漩涡结构,本文采用RNGk-ε模型[8]求解k和ε,该模型在冲刷坑数值模拟中有较好的效果[20]。
2.2 泥沙运动及河床变形模型在冲刷模拟过程中,需要描述床面泥沙的起动条件,并考虑泥沙的悬移和推移运动两种可能的运动模式。
2.2.1 泥沙起动 冲刷坑形成及发展的过程中,局部床面与水流方向非平行,流态为非均匀流,冲刷坑坡面上泥沙起动的临界Shields数与平床时不同,需要对其进行修正。引入量纲一的泥沙粒径d*:

式中:d为泥沙平均粒径;ρs为泥沙颗粒密度;g为重力加速度。均匀流床面泥沙颗粒起动的临界Shields数θcr如下[21]:
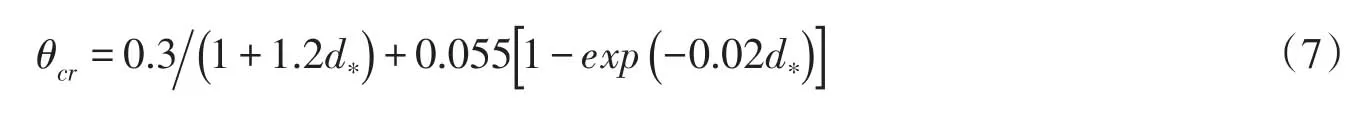
设冲刷坑斜坡面与平床面夹角为β、近床面水流方向与斜坡面上坡方向的夹角为ψ,坡面上泥沙临界起动Shields数修正为θ′cr:

式中:φ为泥沙水下休止角,本文取为32°。
2.2.2 泥沙输运 泥沙的推移质运动主要是求解推移质输沙率qb,这里采用Meyer-Peter推移质输沙率公式[22]:
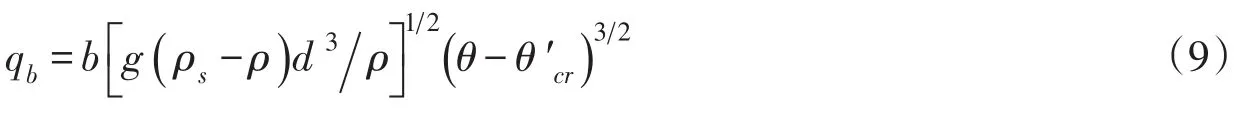
式中:θ为水流的Shields数;b为经验参数,其取值与θ有关,本文取8~12。
悬移质泥沙运动由含沙浓度紊动扩散方程表示[23]:

式中:C为悬移质泥沙浓度;βs=1;ωs为泥沙沉降速度,底部床面边界上的泥沙浓度Ca如下计算[24]:

式中:a=2.5;d为悬移质床面参照高度。悬移质输沙率由浓度与流速乘积的垂线积分得到。
2.2.3 床面变形方程 采用床面质量守恒方程描述床面变形:
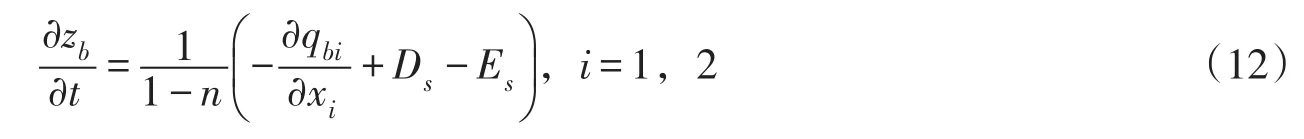
式中:zb为床面高程;n=0.4,为泥沙孔隙率;Ds、Es分别为悬移质泥沙的沉降和卷吸率[23]。冲刷坑演变过程中,还采用沙滑模型修正坡面角度大于泥沙水下休止角的情况[11]。
2.2.4 数值解及边界条件 采用有限体积法对上述方程进行空间离散,以求得数值解。在设置的计算域和坐标系下(如图1所示),方程求解的边界条件类型有水流入口、出口边界、对称边界和固壁边界,图1中h为水深,D为墩柱直径。按对称性处理的边界包括水表面和两侧面。本文计算时,满足h/D>3,属于窄墩[1],且水流弗劳德数Fr较小,此时,自由液面变化对底部床面影响不大[11],故按对称边界处理。两侧面作对称边界处理,以消除边壁对于柱体周围水流的影响。

图1 计算域设置
各类边界条件分别为:(1)在水流入口边界,给定均匀流x方向速度u和紊动能k垂向分布,其分布由紊流模型在图1所示计算域无墩的情况下计算得到,其余方向速度为零;(2)在水流的出口边界上,设各水流速度分量、紊动能和水压力的法向梯度均为零;(3)在对称边界上设置各通量均为零,仅有切向信息;(4)在固壁边界上,设定无滑移条件,即各速度分量和压力为零。悬移质的含沙量在底部Ca按式(11)计算,其余边界上设通量为零。
3 模型验证
3.1 验证条件本文数值模型采用Melville的桥墩冲刷试验[25]进行验证。该试验所用水槽长19 m,宽0.456 m,高0.44 m,直径D=0.05 m的圆柱墩置于水槽中间,断面压缩率B/D=9(其中B为水槽宽度),水槽比降为1×10-4。床面铺中值粒径d50=0.385 mm的均匀沙,泥沙休止角为32°。试验的来流条件为水深h=0.15 m,时均流速U0=0.25 m/s,时均切应力为0.19 Pa,小于泥沙临界起动切应力0.21 Pa。
针对Melville的试验,为减少计算量,建立模型时在保证桥墩周围流态不受影响的情况下,适当设置了计算域的几何长度。设坐标系原点位于床面墩中心,墩柱中心距上游入口长度为6D,距下游出口长度为14D,距计算域两侧面均为4.5D,见图1。床沙厚度设为0.07 m。来流条件与试验相同。
3.2 网格信息网格划分质量对于提高墩周涡流及床面变形的模拟精度非常重要。本文采用六面体网格对计算区域空间进行离散,并在以墩柱轴线为中心,边长为3D×3D×h的局部范围内采用加密网格与嵌套网格相结合,如图2,使墩周流区的水平向网格(图2(a))平均尺寸达到0.05D。
本文还特别地参照底部马蹄涡的形成范围,对控制床面以上第一层网格以及沙层网格高度的设置进行了较多探索。圆柱绕流中当墩雷诺数Re>1×104时,墩柱前马蹄涡中心的x方向位置为0.64D~0.69D,z方向距离床面为0.04D~0.06D[26-27],本工况墩雷诺数为1.27×104,故为了能够刻画马蹄涡,z向第一层网格尺寸设置为0.01D左右,小于涡心距,x-z平面墩周网格的布置见图2(b)。经网格测试计算,最终采用的网格总数量约为80万,其中局部加密区网格数约为24万。

图2 计算网格划分及嵌套示意图
为满足水、沙运动过程瞬态解的稳定和收敛,取时间离散步长Δt始终满足柯朗数小于1。
3.3 验证结果分别针对局部流场和床面变形的结果进行验证,图3为t=0时刻z=2 mm的x-y平面墩周流场。对比图3(a)的流线图可以发现,数值计算和试验测得的墩前绕流及墩后尾涡尺度都几乎一致,水流与墩柱面分离点的位置几近相同。图3(b)为墩周流速相对于来流速度U0的放大倍数即U/U0分布,可以看出,数值计算与试验测得的分布情况吻合良好,其中最大流速为1.2U0,出现在墩侧附近。由于墩柱局部区域流速增大至大于泥沙临界起动流速,局部床面开始发生冲刷,且冲刷坑逐步增大。
图4为t=30 min时刻墩周冲刷深度等值线的对比,可以看出二者的冲刷形态很相近,仅在墩后出现差异,这也是很多数值模拟难以解决的问题[17,28]。该时刻墩周最大冲刷深度出现在墩前,数值计算给出其大小为4.1 cm,与试验测量值4.5 cm相对误差约为8.9%。墩周最大冲刷深度是随时间变化的变量,记为dt,将30 min时刻的最大冲刷深度记为dt30,则在前30 min内dt/dt30随时间的变化趋势如图5所示。可见数模与试验结果吻合良好。
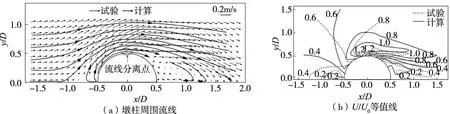
图3 流场验证
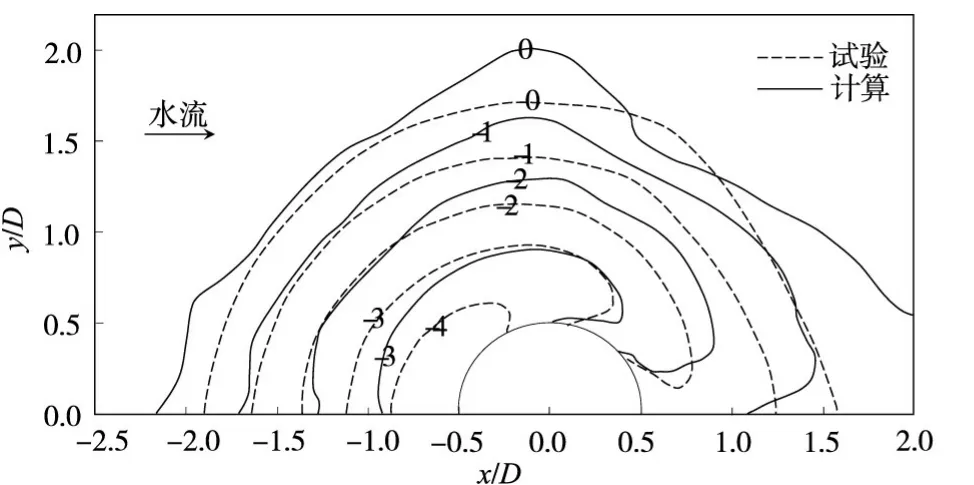
图4 t=30min冲刷深度等值线图(单位:cm)

图5 相对最大冲刷深度随时间的发展

图6 A、B点位置
4 冲刷过程中的悬移质输运与推移质贡献
本文数值模拟考虑了两种不同的局部冲刷状态,即清水冲刷(方案1)和动床冲刷(方案2)。两种方案的计算域设置均同图1,床沙平均粒径均为0.385 mm,方案1的来流与Melville的试验[25]相同,方案2的来流时均流速U0=0.35 m/s,时均切应力τ0=0.36 Pa,满足动床冲刷τ0>τc条件。
在冲刷过程中,紊流场随着墩柱周围床面的变化而不断改变,对泥沙悬移质或推移质的输运能力也将不断改变,即泥沙的两种输运状态对冲刷发展的贡献是变化的。为揭示其过程中两种泥沙输运的贡献,在床面和流场变化最强烈的墩侧平面位置分别选取A(x=0,y=0.75D)和B(x=0,y=1.00D)点(如图6所示),并取两点自水面至床面的垂线,对垂线上的悬移质和推移质输沙率分别进行计算比较。同一垂线上,推移质输沙率qb由式(9)计算,推移层以上悬移质输沙率qs用数值计算点的含沙量和时均流速之积沿垂线积分获得,即:

墩周水流和泥沙运动具有强紊动和随机性,其时均值是采用500个时间步长的瞬态数值计算结果进行平均计算而得。为便于分析,本文设分别为无量纲悬移质和推移质输沙率,并设悬移质输沙率与推移质输沙率之比为时均悬推比η,即:

由式(14)可定量得出两种泥沙输运对冲刷坑发展的贡献。
4.1 清水冲刷条件冲刷坑在初始阶段变化很快,通常在发展至冲刷平衡的前20%时段内冲刷深度约为平衡冲刷深度的80%。现分析冲刷发展较快的前15 min过程中A、B两垂线的q*s和q*b变化,如图7所示。图7(a)为悬移质输沙率随冲刷时间的变化,其中A点因距墩柱近,开始冲刷时输沙率较大,但随时间一致性快速减小;B点的输沙率则呈现先增大后减小的变化。主要是B点在开始冲刷时刻的水流强度小于A点,且冲刷坑尚未发展至此,但随着冲刷坑逐渐增大,该处水流强度及输沙能力增大,当该处床面继续冲刷加深,输沙率则下降。图7(b)为推移质输沙率随冲刷时间的变化,A、B两点的输沙率变化趋势与图7(a)近乎相同,但量值远大于后者,且A点的推移质输沙率减小速率远小于悬移质输沙率的减小速率。

图7 清水冲刷输沙率随冲刷时间的变化
清水冲刷的整个过程中,悬移质输运量占总输沙量的比例很小。图8给出了时均悬推比随冲刷时间的变化,由图8可见,A点悬推比冲刷开始的瞬间最大,在t=0.5 min时,η≈4%;B点悬推比最大值(约为2.5%)较滞后,出现在t=6 min时。在本文清水冲刷条件下,推移质输运在冲刷坑发展过程中始终占控制地位。
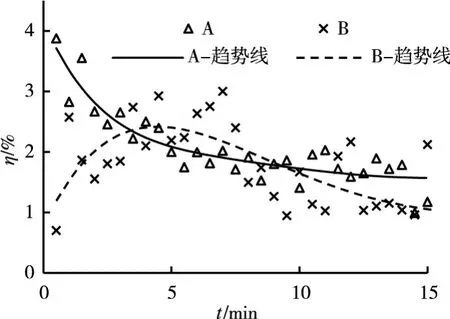
图8 清水冲刷悬推比变化
4.2 动床冲刷条件动床冲刷的冲刷坑较清水冲刷发展快,t=5min时的冲刷坑的最大深度已大于清水冲刷t=30min时刻的最大深度。仍以A、B两点为例,揭示冲刷坑发展过程中的悬移质和推移质输运的变化,如图9。与清水冲刷的输沙率(图7)相比有以下不同:图9(a)悬移质输沙率在A点随时间单调下降,初期时段的下降率很大,主要是起始时刻输沙率很高,B点虽也有先增大后减小的趋势,但增大的时段很短,且初始输沙率很大;图9(b)推移质输沙率随时间的变化在A点与图7(b)趋势相似,但在B点初期随时间增大的时段很短,输沙率在冲刷至1.5 min时达到最大,然后则持续缓慢减小。此工况的悬推比变化过程如图10所示。图中A点和B点的悬推比大小和随时间的变化趋势几乎相同,与图8相比,悬推比增大了1~1.5倍,B点的初始时段变化趋势与图8明显不同。

图9 动床冲刷输沙率随冲刷时间的变化

图10 动床冲刷悬推比的变化
进一步分析可知,动床冲刷与清水冲刷两种条件的来流时均切应力之比为1.89,而最大悬移质输沙率之比则达约10.0(A、B点基本相同),最大推移质输沙率之比在A点约为2.9,在B点约为2.3。可见悬移质和推移质输沙率增长率大于来流强度增长率,而悬移质输沙率增长率为来流强度增长率的数倍。
5 泥沙运动状态与水流特征量的相关性

图11 清水冲刷过程的墩侧横断面涡量(单位:1/s)

图12 动床冲刷过程的墩侧横断面涡量(单位:1/s)
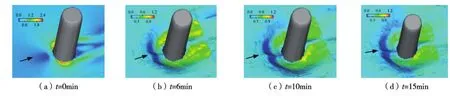
图13 清水冲刷过程中墩周床面切应力分布(单位:Pa)
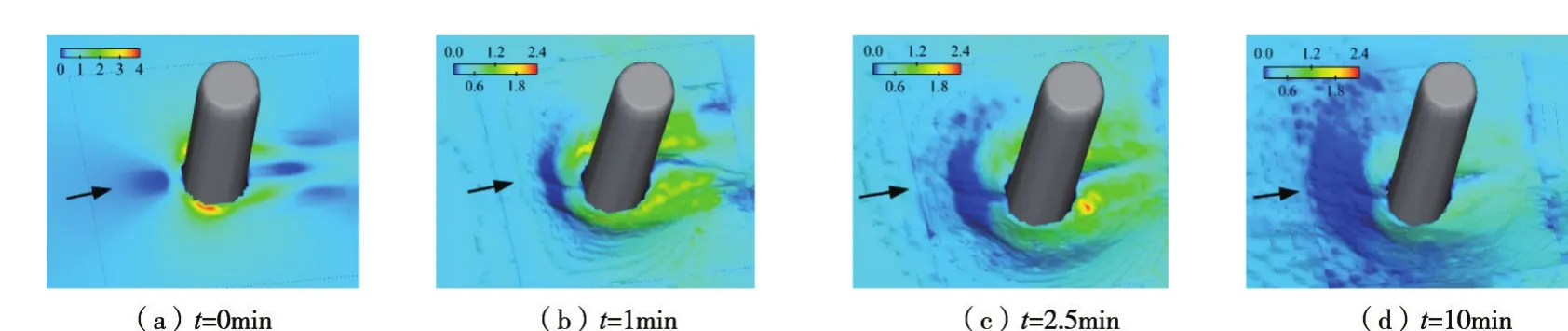
图14 动床冲刷过程中墩周床面切应力分布(单位:Pa)
墩柱周围具有马蹄涡流特征,很多文献针对墩前对称面进行了研究,本文着重讨论冲刷过程中墩侧沿柱中心横剖面的涡量、切应力与泥沙输运的相关性。
5.1 马蹄涡作用马蹄涡的动力特征采用涡量描述,总涡量ω在各方向上的分量ω按如下计算:

在墩侧过墩柱中心的横断面上,清水冲刷和动床冲刷过程中几个特征时刻的总涡量ω分布分别如图11和图12。图11(a)和图12(a)均为t=0(冲刷起始)时刻,清水冲刷和动床冲刷悬移质输沙率最大的时刻分别为t=6 min和t=1 min。计算垂线平均涡量可知,图11和图12中A垂线的平均涡量随时间衰减,B垂线的平均涡量则由(a)到(b)增大,由(b)到(d)减小,与输沙率的变化趋势一致。
5.2 床面切应力冲刷坑发展过程中水流床面切应力变化见图13(清水冲刷条件)和图14(动床冲刷条件),t=0时刻墩柱周围切应力最大,图13(a)中τmax=2.4 Pa,图14(a)中τmax=4.0 Pa,均位于与迎流方向交角约45°处。在随冲刷坑发展过程中,最大切应力迅速减小,且其位置移向下游。在清水冲刷的t=0~6 min时段和动床冲刷的t=0~1 min时段床面切应力减小速率大,后续切应力减小速率变缓,如图13(b)—(d)和图14(b)—(d)。分析发现,墩侧面A、B床面切应力与输沙率变化趋势一致,与悬推比η具有相关性,见图15。
墩柱周围床面切应力较来流增大,与局部马蹄涡流态有关。对A、B两点清水冲刷和动床冲刷两种条件计算的垂线平均涡量与床面切应力进行分析,得到涡量与切应力关系如图16所示。
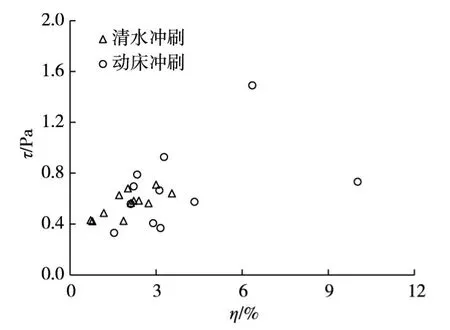
图15 切应力与悬挂比关系
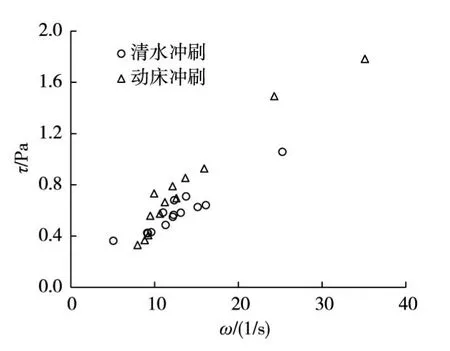
图16 涡量与床面切应力关系
5.3 悬移质输运贡献与悬浮指数悬移质输沙率与悬浮指数Z有关:

式中:κ=0.4为卡门常数;u*为摩阻流速。本文根据冲刷过程中数值计算的床面切应力,由下式计算相应的摩阻流速:

进而可计算悬浮指数Z。通过由床面切应力计算的悬浮指数,可探讨墩柱局部冲刷过程中悬移质输运贡献与悬浮指数的关系。设ξ为悬移质输沙率qs与总输沙率qt之比,其值表示悬移质输沙率贡献,即:

式中qt=qs+qb。取本文两种计算方案Case1和Case2冲刷过程中A、B点所在垂线计算得到的ξ与Z点绘在图17中,其中还绘入了Laursen曲线及前人的试验结果[24]。从图17可见,本文计算结果与Laursen曲线趋势很接近,d=0.19 mm的前人试验数据当u*/ωs>1时与Laursen曲线较符合,见文献[24]。
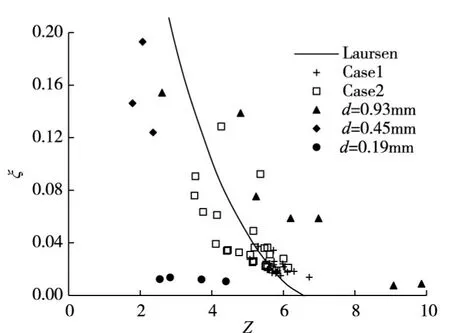
图17 悬浮指数与悬移质输沙贡献比
图17表明冲刷过程中悬移质输运的贡献与悬浮指数明显相关。清水冲刷过程中的水流切应力、涡量及摩阻流速均较动床冲刷时小,Z在5.1~6.8之间,数值相对较大,悬移质输运贡献小,ξ<4%;动床时则因水流动力增大,Z在3.5~6.2之间,数值相对较小,悬移质输运贡献增大,ξ在2%~13%之间。本文计算的条件下,尽管是动床冲刷,其悬移质输沙率贡献最大也仅为13%,因为本文的动床条件的来流切应力刚达到泥沙起动临界值,τ0/τc=1.7,本研究还模拟了条件τ0/τc=11.2局部冲刷,此条件的冲刷坑发展过程中,悬移质贡献最大可达45%。因此,无论是清水冲刷还是动床冲刷,悬移质输运对墩柱局部冲刷坑发展的贡献大小与悬浮指数大小有关。但清水冲刷条件下,悬移质输运对局部冲刷坑发展的贡献很小,数值模拟时可予以忽略,以节省计算时间,动床冲刷是否考虑悬移质输运,可视悬浮指数决定。
6 结论
本文利用URANS方程、考虑悬移质和推移质输运的水、沙运动和河床变形方程,以圆柱墩为例进行了结构物局部冲刷数值模拟,讨论了清水冲刷和动床冲刷来流条件下,墩柱局部冲刷坑发展过程中的局部涡流、床面切应力、悬移质和推移质输沙率的变化,基于水、沙量变化关系讨论了悬移质和推移质输运在冲刷过程中的贡献,回答了局部冲刷数值模拟是否考虑及如何考虑悬移质泥沙输运的问题,得出以下主要结论:
(1)最大的悬移质和推移质输沙率都发生在局部冲刷坑发展的早期时段,且随冲刷坑的增大而迅速减小,在冲刷发展至平衡的后80%时段内,输沙率缓慢降低。
(2)结构物周围局部冲刷是强三维和时变问题,冲刷坑的形态与发展决定了水流的变化,水流作用决定了床面泥沙运动,各空间点悬移质和推移质输沙率与水流的床面切应力的变化趋势存在很强的相关性,墩周局部马蹄涡导致床面切应力的增大,涡量与床面切应力呈正相关关系。
(3)无论是清水冲刷还是动床冲刷,悬移质输运对局部冲刷发展的贡献大小决定于坑内由床面摩阻流速表示的悬浮指数,悬移质输沙率的贡献,在悬浮指数大于5的范围内小于5%,但随悬浮指数的减小迅速增大。
(4)清水冲刷条件下,冲刷坑内床面悬浮指数通常较大,悬移质输沙率的贡献率较小,局部冲刷数值模拟中可不考虑,以节省计算时间;满足动床冲刷条件的局部冲刷发展过程中,悬移质输沙的贡献大小与局部床面的悬浮指数有关。

