冲泻区形态动力学耦合模型研究Ⅱ：模型建立与验证

邓 斌，蒋昌波，陈 杰，杨树清

（1.长沙理工大学 水利工程学院，湖南 长沙 410114；2.水沙科学与水灾害防治湖南省重点实验室，湖南 长沙 410114；3.长沙理工大学 水科学与环境工程国际研究中心，湖南 长沙 410114；4.School of Civil，Mining and Environmental Engineering，University of Wollongong，Wollongong，Australia 2522）

1 研究背景

冲泻区是由短波和长波引起的水位波动交替覆盖和暴露的海滩区域，充分了解该区域水沙动力特性对研究岸滩侵蚀机制和海岸洪水运动规律至关重要[1]。由于该区域进行水动力[2]和岸滩演变[3]测量非常困难，对冲泻区高瞬态、薄层、湍流和多相流等水动力特征及其与床面相互作用机制的认识非常有限。在近期举办的第二届冲泻区国际研讨会上，众多学者一致认为关于渗流对冲泻区沉积物输运的影响以及形态变化的模拟仍然是研究的重点。

近十年，随着计算机技术进步，冲泻区水动力学数值模型也得到了广泛发展[4]。学者们基于雷诺平均N-S 方程[5]、大涡模拟[6-7]、浅水模型[1，8-9]和边界层模型[10]等，开展了冲泻区水动力特性的研究，对水深与流速的时空分布、岸线轨迹、紊动、波浪爬高、压力梯度、边界层流动等方面有了一定的认识。这些研究主要集中在冲泻区水动力学数值模型上的改进[1]，较少关注泥沙输运和岸滩形态的数值研究[11]。

目前冲泻区形态动力学的数值研究，主要采用基于浅水非线性方程（NSWEs）的水深平均模型和简化泥沙输运公式相结合来模拟[1]，为掌握岸滩形态演变规律提供了有价值的成果。但这些模型中，部分为定床模型，仅考虑其水动力特性，忽略床面摩阻、泥沙运动以及岸滩形态的影响；部分为动床模型，一定程度上考虑床面摩阻以及床面变形的影响，但忽略了冲泻区内复杂的水沙运动特性，如泥沙输运采用简单的经验公式、忽略岸滩水流出渗/入渗效应等；同时，这些模型存在数值处理格式相对简单、激波捕捉格式精度较低的问题，难以很好揭示冲泻区内复杂水沙运动的普遍规律和动力特性[12]。

另一方面，冲泻区的水流、泥沙运动及床面变形均有相对独立的特征时间尺度，属于典型的多重时间尺度问题，其求解方法主要有非耦合数值解法和耦合数值解法两种[13]。非耦合数值解法是在每个时间步骤内顺序求解水流和床面变形方程[14-15]，由于冲泻区内水沙运动的高瞬态性，该方法尚不能充分描述水流与泥沙运动之间的相互作用机制。而耦合数值解法是同步求解水流和床面变形方程，在每个时间步内都计算水流和泥沙运动的特征参数值[16-18]，可有效解决上述问题。因此，充分考虑冲泻区物理过程并结合耦合数值解法是当前开展冲泻区形态动力学模拟的有效方法[9，13]。本文将基于分段输沙率公式[19]，建立冲泻区水动力及其岸滩形态动力学耦合分析模型，进一步研究冲泻区水流与泥沙运动之间的相互作用机制。

2 模型基础

冲泻区内水深较浅，采用非线性浅水方程（NSWEs）能较好地描述冲泻区内的水流运动特性[9]。因此，本研究基于1D NSWEs并结合床面变形Exner方程建立耦合分析模型。采用无量纲量来描述岸滩形态动力学理论模型：

式中：x为水平坐标；t为时间；h为水深；l为参考长度；u为水深平均速度；q为输沙率（为h和u的函数）；h0为参考长度；q0为输沙率参考尺度；g为重力加速度。为方便书写，无量纲变量x*（水平坐标），t*（时间），h*（水深），u*（水深平均速度），B*（床面高程），q*（推移质输沙率，为h和u的函数），分别采用x，t，h，u，B表示，则控制方程为：

3 模型建立

3.1 输沙率公式首先考虑两类广泛应用于冲泻区的输沙率公式，即分别为假定推移质输沙率为流速的函数q（u）与推移质输沙率为流速和水深的函数q（h，u）。其次，采用已建立冲泻区分段输沙率公式封闭床面变形方程[19]。为便于计算分析，将6种推移质输沙率公式均统一按q=q（h，u）的形式进行处理。表1给出不同输沙率公式qb的量纲形式和无量纲形式，以及对应控制方程（2）—（4）中的q0、qh、qu和σ。6种输沙率公式中的床面可动性参数A的取值详见文献[21]。

3.2 床面剪切应力现有考虑床面摩阻影响的剪切应力公式认为摩阻的影响相当于等效阻力，常采用半经验公式（如：曼宁阻力公式、谢才公式）描述，其中采用谢才公式计算床面剪切应力在具有振荡流特性的破碎区和冲泻区获得了较好结果[25]。本文亦采用谢才公式概化计算床面剪切应力：

表1 不同输沙公式表达式及相关变量

式中：CD为阻力系数；h为水深；u为水深平均流速。

则原控制方程式（3）可改写为：

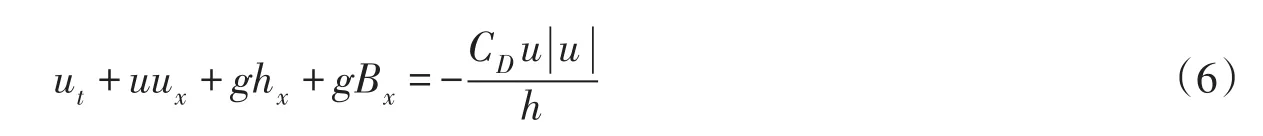
式（6）中，在岸线位置，由于h→0，则对于冲泻区的水流上爬阶段，参考Antuono等[26]对岸线附近床面剪切应力项的处理方法，该项可通过hx平衡，即在波前处hx→-∞。在水流回落阶段不能通过hx平衡；当u＜0时但不满足hx→∞。因此，仅当u=0时，在水流回落阶段，求解方程在岸线位置才成立。在水流上爬和回落阶段，由于岸线位置不同，因此在数值处理时，可参考Zhu[9]在水流上爬阶段采用外推法计算波前速度，在水流回落阶段令岸线处u=0。

3.3 渗流源项现有岸滩形态动力学模型的研究多数忽略了渗流（含水流出入渗和冲流加减速产生的垂向流速）的作用。参照Delestre等[18]在坡面流数学模型中考虑降雨入渗的处理方式，在控制方程中考虑渗流源项：

式中：w为渗流流速，w＞0时表示水流出渗，w＜0时表示水流入渗。同时，对应动量方程中，也应体现渗流存在而引起的动量变化，即式（6）可进一步改写为：

3.4 控制方程及数值耦合求解方法进一步考虑底坡、床面剪切应力、渗流等源项可得到描述冲泻区水沙运动物理过程的模型控制方程：

为实现对上述方程的耦合求解，需同时考虑水流与床面变形的求解。由于上述控制方程可写成不同的守恒形式，参考Hudson[28]对四种耦合求解方式下的计算结果，当在（hB）x=hBx+Bhx的形式下能得到较精确的结果。本文运用Hudson的做法，模型耦合求解的矩阵形式可写为：

式中：U为守恒变量；F为x方向的通量；S为源项，分别为：

基于有限体积法数值离散上述守恒形式的方程组（13），令空间和时间区域属于（x，t）∈（I，[0，T]），空间步长设为Δx，单元中心节点为xi=i×h，i=0，…，N，所分割单元为Ii=[xi-1/2，xi+1/2]。时间步长为Δxt=tn+1-tn，时间离散为0=t0＜t1＜t2＜…＜tn+1＜…＜tN=T，则时间分割单元为[tn，tn+1]。根据上述网格划分，则各单元变量在时间tn的平均值为：

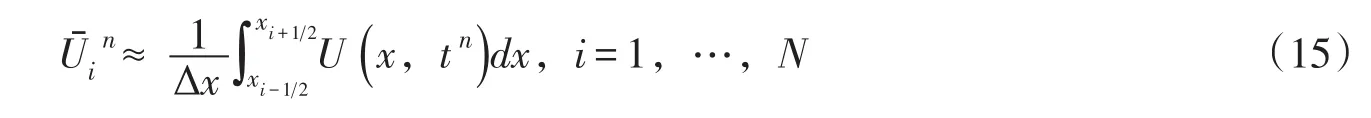
对式（13）在空间时间区域上（x，t）∈（I，[0，T]）进行积分，得到有限体积的离散形式：

运用式（15），式（16）可写成：

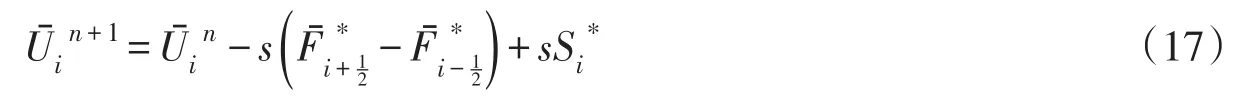
4 数值模拟验证

4.1 床面形态变化验证——沙坝算例为检验数值方法计算地形变化的有效性，选取经典的“沙坝算例”[30]进行模型验证。初始条件设置如图1所示，设置长2000 m的计算范围，并在床面附近设置一个小沙坝，其无量纲初始地形表达如式（18）所示，计算时忽略床面剪切应力和渗流的影响。

图1 沙坝算列

式中：Δ=B/h0为地形无量纲扰动振幅。其中，参考长度尺度取B0，入口流速尺度为u0，时间尺度取Ts=（B0/g）1/2。计算参数设置如下：Δ=0.1，xL=2000 m，u0=1 m/s，h0=10 m，其他参数设置与Hudson等[30]和Postacchini等[31]保持一致，计算网格取Δx=2 m。

图2为t=186070 s的地形变化结果。可见，采用TVD-WAF格式计算，在沙坝迎水面和背水面与解析解吻合较好，特别是在沙坝波峰处（x=570 m），TVD-WAF格式计算的结果与解析解非常接近，计算值与解析解的均方根误差RSME=0.019，可应用于后续的相关计算。

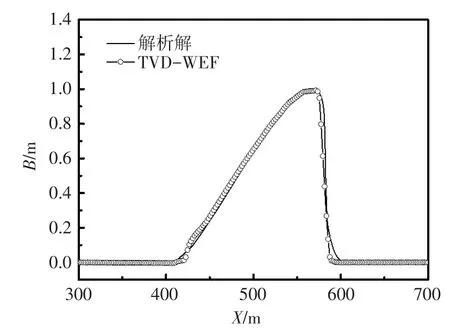
图2 地形变化结果（t=186070 s）

图3 不同输沙公式下地形变化结果（t=186070 s）

为检验不同输沙率公式对结果的影响，计算分别采用了表1中6种输沙率公式，计算结果如图3所示。从图中可见，采用q（u）形式的输沙率公式时，Grass、Van Rijn、Bagnold和Meyer-Peter Müller等输沙率公式计算得到的结果基本一致，且均与近似值接近，对应的均方根误差RSME值分别为：0.0505、0.0605、0.0565和0.0221；采用q（h，u）形式的输沙率公式（如Pritchard&Hogg输沙公式）计算得到的结果局部稍偏离采用q（u）形式的计算结果以及近似解，在x=400 m附近计算结果出现负值，在沙峰位置大于其他公式的计算值，且沙坝的整体移动要慢于其他公式，计算得到RSME值为0.0937。采用分段输沙率公式[19]计算得到结果与q（u）型输沙公式基本一致，但在沙坝背水面优于q（u）型输沙公式的计算结果，对应的RSME值为0.0296。

4.2 ZD13 岸滩剖面变化数值模拟Zhu 和 Dodd[32]（下文简称 ZD13）在 Peregrine和 Williams[8]（简称PW01）的基础上，基于特征线理论建立了一维岸滩形态动力模型，数值模拟PW01问题，并与PW01解析解进行对比。由于PW01解析解是基于定床得到，ZD13通过假定床面可动系数σ=1×10-7进行数值验证，并在此基础上进行动床条件下的数值模拟。本研究以PW01问题为基础，考虑分段输沙率公式及有无床面剪切应力作用，数值模拟单次冲流事件下冲泻区内岸滩剖面的变化，并与ZD13的研究进行对比，验证模型的可靠性。

图4 单次冲流事件下冲泻区概化计算模型（ZD13）

图4给出了ZD13的概化计算模型，数学模型设置均与ZD13问题完全一致，令岸滩坡度λ=0.1，则床面高程B=γx，在x=0处把岸滩左侧定为碎浪区，右侧为冲泻区。左侧初始水深为h（x＜0，t=0）=1，速度u（x＜0，t=0）=0，右侧初始水深与速度均设为0，并假定海侧边界x=-250 m，h（-250，t）=1，B（-250，t）=-250γ，u（-250，0）=0，u（-250，t）=-γt。计算首先考虑无床面剪切应力作用，即令CD=0（ZD13假定曼宁系数n=0），网格取Δx=0.002 m，时间步长取Δt=0.0002 s。

图5为计算得到的无量纲水深、流速和床面变化值的时空分布与ZD13的结果对比。从图中可见，当采用与ZD13一样的输沙公式时（即q=u3），本研究计算得到的h、u和ΔB与ZD13的计算结果基本一致。结果表明泥沙在水流上爬阶段是向岸运动，在高冲泻区产生淤积，而在回落阶段更多的泥沙离岸运动，导致中冲泻区和低冲泻区被冲刷，与本研究实验观测到的现象以及与Jiang等[7]通过对冲泻区水动力特性进行数值计算预测得到的冲淤趋势相吻合。

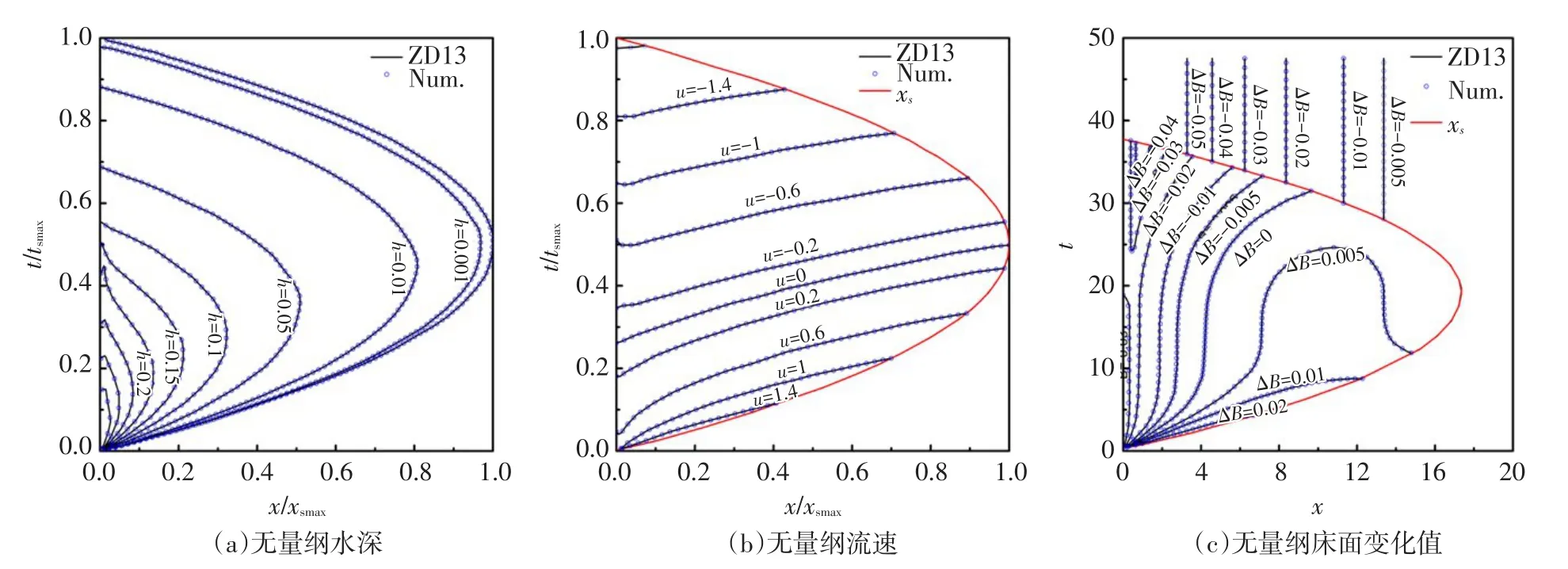
图5 无量纲水动力参数计算结果的时空分布与ZD13的结果对比

为研究床面剪切应力对岸滩形态变化的影响，采用3种不同的阻力系数（CD分别取0、1×10-3和1×10-2），其他初始条件设置保持不变。图6为3种不同阻力系数下，计算得到的地形变化值与ZD13的计算值对比。其中ZD13的结果为2个工况（输沙率公式分别为q=u3和q=hu3）计算值，ZD13的计算结果显示，采用输沙公式q=u3时，岸线附近的地形变化值较采用q=hu3得到的计算值小，高冲泻区无明显的淤积。而采用q=hu3计算得到高冲泻区会产生少量淤积，这是由于公式q=hu3包含h和u的影响；在水流回落阶段，高冲泻区内水深和流速的逐渐减小会导致该区域较少的泥沙离岸输运。从图6可以看出，当阻力系数CD增大、对应床面阻力增大时，各计算工况得到的地形变化值随之降低，即冲刷量均随床面阻力的增大而变小，同时最大爬坡高度也随之减小。值得注意的是，在不考虑床面剪切应力时（CD=0），采用q=hu3计算得到的最大爬坡高度达到26.34，即在岸线后出现一条狭长的薄层水流，而考虑床面剪切应力作用（CD≠0）会限制薄层水流的发展，从而导致水深增加，爬坡高度减小。ZD13采用两种不同类型的输沙率公式计算得到的结果具有明显差别，表明在冲泻区不同位置考虑不同的输沙率公式，是精确模拟冲泻区岸滩形态变化的有效途径。

图6同样给出了采用本文分段输沙率式在不同阻力系数下的岸滩地形变化值。从图中可见，在岸线附近，计算值与ZD13采用q=u3计算得到结果接近，在高冲泻区的计算值与ZD13采用q=hu3计算得到的结果基本一致，表明了本模型计算结果能充分反映低、中冲泻区输沙强度由流速主导、高冲泻区输沙强度由水深主导的内在机制。

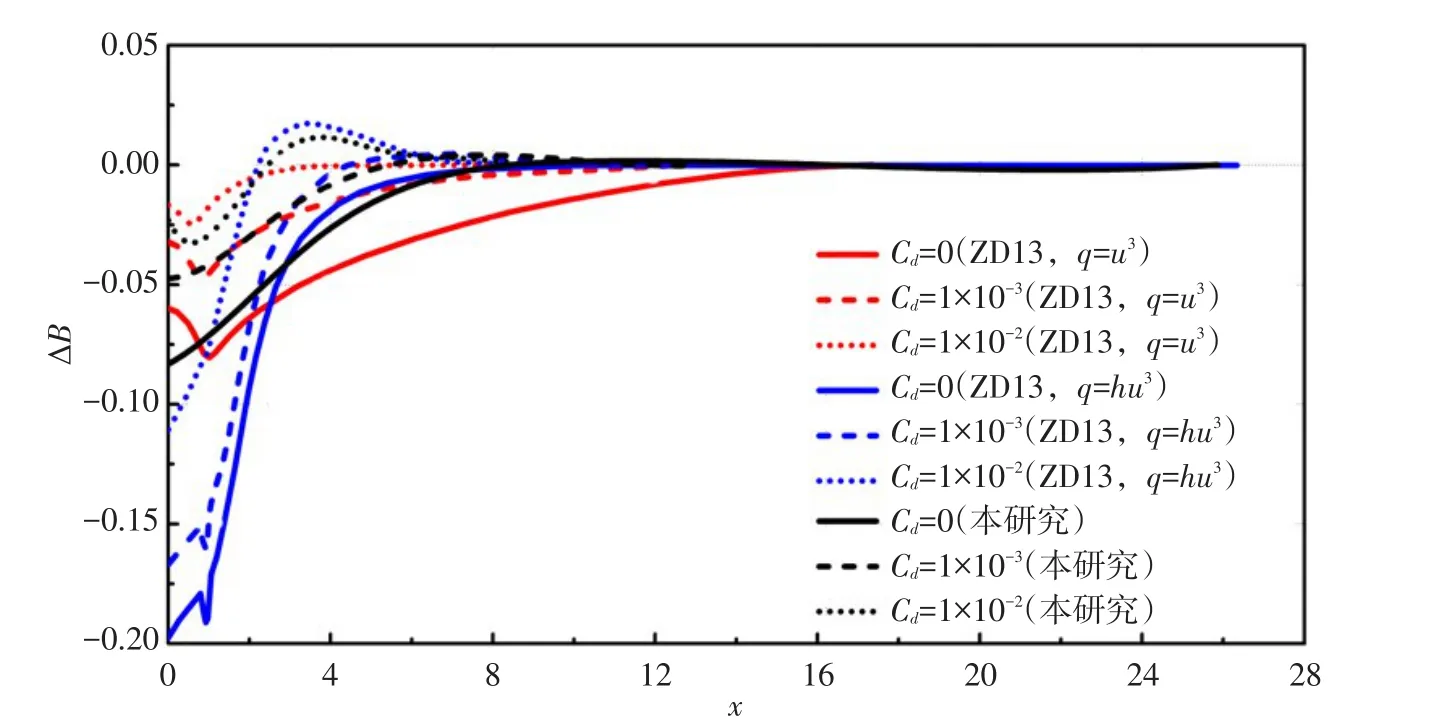
图6 不同阻力系数下本文计算得到的地形变化值与ZD13的计算值对比

4.3 实验条件下岸滩剖面变化数值模拟基于邓斌[21]的实验数据，开展相应实验条件的泥沙运动与岸滩演变研究。主要分析以下两种情况：一是考虑摩阻系数是否为常数对计算结果的影响；二是考虑有无渗流对计算结果的影响，进一步评估模型在源项改变时的适应性。

数值模拟工况与实验布置完全一致。计算网格取Δx=0.002 m，时间步长取Δt=0.0002 s，摩阻系数取CD=0.01，无渗流作用（w=0 m/s）。此外，为简化研究，输沙率公式中泥沙代表粒径均以中值粒径表示。图7为数值模拟得到的3个工况下不同断面平均水深计算值与实验值的对比。图8为数值模拟得到的3个工况下岸线轨迹计算值与实验值的对比。可见，数值结果与实验值吻合较好，表明所建立的数学模型能适用于冲泻区水动力特性的模拟。

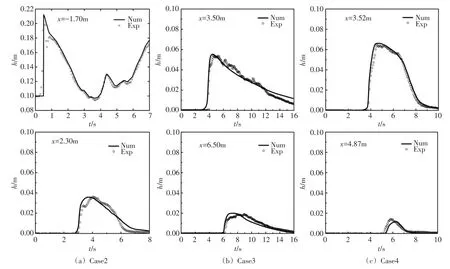
图7 3个工况下不同断面平均水深计算值与实验值对比

图8 3个工况下岸线轨迹计算值与实验值的对比

4.3.1 不同摩阻系数对岸滩剖面变化的影响 前人计算结果表明将阻力系数CD设为常数可获得较好结果，但部分学者认为在冲泻区中采用常数形式的床面摩阻系数CD计算床面剪切应力是不合适的[1]。Barnes等[33]通过现场观测发现摩阻系数在水流上爬阶段约为回落阶段的2倍，即CDu≈2CDb，其中CDu和CDb分别表示水流上爬和回落阶段的摩阻系数，因此本研究分别考虑水流上爬和回落阶段摩阻系数采用不同的取值。考虑到实验基于定床得到水流上爬和回落阶段的摩阻系数相比Barnes等[33]等通过现场研究得到的结果偏于保守，因此取CDb=0.5CDu。同时，为保证床面泥沙运动的一致性，床面可动性参数需满足σb=（CDb/Cd）3/2σ，即q∝τ3/2[23]。

数值模拟工况与上述验证工况完全一致，源项仅考虑底坡和床面剪切应力的影响。图9为动床3个工况第一次冲流后，分别考虑CDu=CDb=0.01和CDu=2CDb=0.01两种不同摩阻系数影响下的岸滩剖面改变的计算值与实验值对比，Case2下计算得到RSME值分别为0.0003和0.0024，Case3下计算得到的RSME值分别为0.0017和0.0017，Case4下计算得到RSME值分别为0.0024和0.0023，可见数值模拟结果与实验值吻合较好，模型考虑CDu=2CDb=0.01时，计算值与实验值更为接近。在单次冲流事件后，岸滩剖面变化均较小，Case2下岸滩剖面呈沙坝形状，在静水面以下（x=0.45～0.75 m）出现淤积，在低冲泻区和中冲泻区均出现冲刷，高冲泻区略有淤积，Case3和Case4下冲刷和淤积均较小，地形变化不够明显。

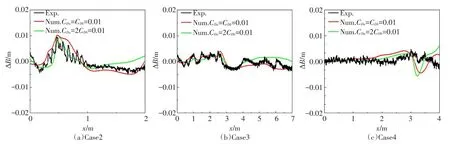
图9 不同摩阻系数下岸滩剖面改变量的计算值与实验值比较

计算中分别采用水流上爬阶段和回落阶段不同床面摩阻系数与同一摩阻系数，对比两种计算结果表明，前者计算得到的淤积沙坝高度相对较小，在低、中冲泻区的冲刷也相对较少，并在高冲泻区呈现薄层的淤积，与实验观测到的现象一致。当水流回落阶段床面摩阻小于水流上爬阶段时，由于阻力的减少，回落水流向岸运动更快，将会导致更多的泥沙离岸运动，冲刷将会增大；然而，水流回落阶段σ的减少将会使泥沙运动减少，从而导致较少泥沙离岸输运，在整个周期内淤积增大。当采用CDb=0.5CDu时，沙坝淤积量有所减少，低、中冲刷量略有减少，在高冲泻区淤积量有所增大，这表明CD和σ的联合改变导致岸滩冲刷量减少，在高冲泻区会产生净淤积。因此在冲泻区岸滩形态变化模拟时，考虑不同的床面剪切应力是非常有必要的。

4.3.2 有无渗流对岸滩剖面变化的影响 为讨论渗流对岸滩剖面变化的影响程度，利用实验数据并结合数值模拟进行定性分析。数值模拟以Case2为例，源项完全考虑底坡、床面剪切应力和渗流的影响，其中床面剪切应力项中摩阻系数按CDb=0.5CDu计算。在原实验条件下，在整个冲流周期内岸滩出现了水流入渗现象，但未出现明显的出渗现象[19]。因此，在水流上爬和回落阶段均只考虑水流的入渗作用，且其取值假定为常数，w的取值采用平均值，即w=-0.001 m/s。

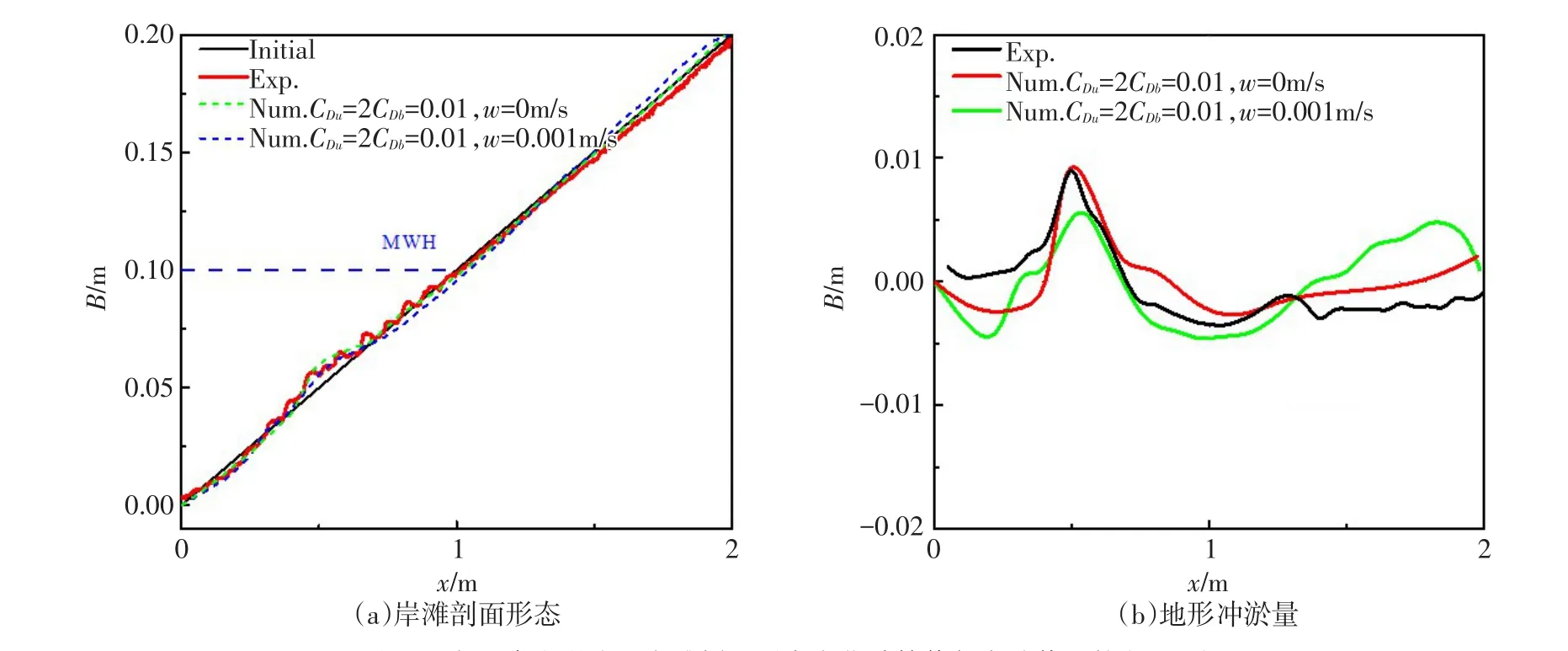
图10 有无渗流影响下岸滩剖面形态变化计算值与实验值比较（Case2）

图10分别为Case2第一次冲流后，分别考虑有无渗流影响下（w=0 m/s和w=-0.001 m/s）的岸滩剖面形态与地形冲淤量的计算与实验值对比。从图10可以看水流入渗下，岸滩剖面分布在高冲泻区呈现较明显的淤积，沙坝区淤积量则略有减少，在低、中冲泻区的冲刷量稍有增加，表明水流入渗情况下，泥沙向岸输运量相应增加，离岸输运则有所减少，与Butt等[34]、Masselink和Li[35]和Li等[36]等的结果趋势一致，进一步说明渗流对岸滩形态的变化存在影响。但图中计算值与实验值存在一定的差异，这是由于计算中仅概化渗流为入渗，未全面考虑实际渗流的沿程变化。因此，有必要进一步获取整个冲泻区岸滩渗流流速特征，为公式的完善提供更全面的基础数据。

4 结论

本文基于一维非线性浅水方程和床面变形方程，进行了冲泻区水动力特性和岸滩形态变化耦合求解模型的研究，主要结论如下：

（1）基于一维非线性浅水方程和床面变形方程，考虑两类（共6种）不同输沙率公式，增加了床面剪切应力源项和渗流源项，建立了描述冲泻区复杂水沙动力特性的岸滩形态动力学耦合计算模型，并对模型可靠性进行了验证。

（2）采用分段输沙率公式，模拟分析了单次冲流事件下冲泻区内岸滩剖面形态变化。模型计算得到的水深、流速和床面形态特征等与ZD13的结果基本一致。计算结果能充分反映低、中冲泻区输沙强度由流速主导、高冲泻区输沙强度由水深主导的内在机制，计算结果较ZD13的结果更为准确。

（3）数值模拟了溃坝波作用下冲泻区水动力与岸滩剖面形态变化。计算得到的水深、岸线轨迹和岸滩剖面变化结果与实验结果吻合良好。床面剪应力源项的改变对冲泻区的水沙动力变化影响较大，冲泻区内岸滩形态变化应充分考虑水流上爬和回落阶段摩阻系数的不同以及渗流的影响。

研究建立的岸滩形态动力学模型为一维模型，下阶段有必要考虑更高精度的数值求解格式和紊流模型，基于气、液、固三相流的完全耦合数学模型是未来的研究方向。