水库型堆积层滑坡位移方向协调性参数及其失稳判据研究

郭 璐，贺可强，贾玉跃

（青岛理工大学 地质环境与效应研究中心，山东 青岛 266033）

1 研究背景

重大水利工程特殊的工程特点与复杂的水环境条件决定了水库型滑坡具有潜在巨大的危害性，国内外由于水利工程修建而诱发的水库型滑坡时有发生。王士天等[1]列举了国内9个水利工程的岸坡失稳实例，Riemer[2]在专题报告中列举了60个水库型滑坡实例，国际大坝委员会水库滑坡专委会在其总结报告中列举了105个水库型滑坡实例[3]。由此可见，水库型滑坡灾害在已建水利工程中具有一定的普遍性。据不完全统计，自2003—2017年三峡水库蓄水期间，由于库区水环境条件产生了变化，库区共出现地质灾害险情132起，多处滑坡变形强烈，一旦发生大规模失稳，将对人民生命及财产安全造成巨大威胁，甚至可能会阻断长江航道，迫使滑坡区居民紧急疏散及转移[4]。

在三峡库区各类库岸滑坡地质灾害中，堆积层滑坡约占滑坡总数的64%，是水库型滑坡的主要类型[5]。由于水库型堆积层边坡特殊的变形特点，一直以来评价该类边坡稳定性都是采用位移预测方法。自日本学者斋藤[6]提出斋藤迪孝法这一位移预测方法以来，国内外学者对边坡稳定性的位移预测方法展开了大量研究。Hoek等[7]提出了预测边坡失稳时间的外延法；张倬元等[8]对十余个岩体失稳边坡的位移-时间曲线进行分析与总结，提出了黄金分割预报法；Fukuzono[9]研究了滑坡的蠕变规律，发现在第三蠕变阶段滑坡位移呈现指数增长规律，并由此建立了滑坡位移-时间预测模型；苏爱军等[10]在斋藤模型的基础上，提出了更适合于加速蠕变规律的修正斋藤模型；伍法权等[11]提出了滑坡位移动力学预测方法；Kim[12]通过有限元分析得出了滑坡发生前坡体位移会出现显著变化的结论；Rutledge等[13]通过对纽约一个大型滑坡进行实时监测，发现监测过程中滑坡前缘监测点的位移有逐渐增大和突变的规律；李天斌[14]根据边坡动态数据时间序列分析法的建模思想，提出了滑坡动态跟踪预测的方法；贾明涛等[15]在对边坡位移可视化系统研究的基础上指出，边坡坡体位移是既有大小，也有方向的三维矢量；Ma等[16]对浸水软化凝灰岩的应变速率及应力-应变特征进行了系统试验研究，发现材料的非线性变形大小和体积扩容率与两个临界破坏阈值应力值密切相关；许强等[17]系统分析了滑坡的累计位移、位移速率与位移加速度的变化规律，提出了基于位移加速度的滑坡预警方法；秦四清等[18]提出了滑坡蠕变破坏与脆性破坏分析预测的2个指数律；张正虎等[19]在时间序列分析法和灰色理论的研究基础上，将两种方法理论相结合建立了一种改进的灰色-时序分析时变预测模型；Belle等[20]基于滑坡降雨与位移关系的研究，提出了一种滑坡稳定性预测的逆建模方法；周超等[21]分析了边坡位移序列混沌特性，在此基础上提出了基于混沌时间序列的WA-ELM滑坡位移预测模型；张凯翔等[22]提出了一种结合小波变换、粗糙集算法与支持向量回归机的滑坡位移预测方法。徐兴华等[23]以滑坡变形时间序列为基础，构建分形预测模型，对滑坡稳定性进行预测。

上述国内外研究现状表明，当前水库型堆积层边坡稳定性评价与预报方法在理论深度与研究广度上都已取得诸多有价值的研究成果。然而由于水库型堆积层滑坡的复杂性，广大学者对滑坡灾害系统位移信息的“多源性”未引起足够的重视，所建立的预测模型常常只将单维度位移量参数作为建模基础与失稳判据准则。然而从“信息论”角度来看，水库型堆积层滑坡单维度位移量预测参数与判据体系无法全面、完整刻画和反映滑坡位移多维度矢量场的动力演化灾变机理与规律，因为边坡单维度位移量参数的变化不仅与其稳定性状态有关，还直接受水动力变化的影响与控制，从而导致该类方法所依据的位移时序曲线在水动力的变化影响下具有极强的非线性、多解性和不确定性。而边坡稳定性演化及其有效的失稳前兆信息应该是边坡位移和位移方向的多维参数的变化。因此，研究和建立边坡位移多源信息参数与预测理论将会大大提高对该类滑坡预测预报的准确性。为此，本文在全面完整认识和确定滑坡位移量与多维度位移矢量场时空演化灾变机理与规律基础上，提出垂直位移方向率这一位移方向协调性参数，并系统研究其与水库型堆积层边坡稳定性演化的关系，以期提高该类滑坡位移预测预报的准确率。

2 水库型堆积层边坡垂直位移方向率及其动态特征分析

2.1 水库型堆积层边坡垂直位移方向率的基本特征对于以次生岩土堆积体为主的水库型边坡，库水位升降及降雨是影响其稳定性的主要因素。库水及降雨入渗引起地下水位升降，导致滑带土体抗剪强度降低，另外还产生孔隙水压力，进而影响水库型堆积层边坡的稳定性。因此，库水位升降及降雨必然引起水库型堆积层边坡的动力改变与位移变化。由于该类边坡坡体结构疏松，其单维度位移量参数的变化不仅取决于水库型边坡稳定性阶段与状态，还直接受水动力变化的影响与控制，且位移变化量与库水位及降雨的变化规律具有明显的一致性和密切相关性。该类边坡水动力的变化和突变常导致边坡位移的波动变化与局部突变，然而边坡位移的变化与突变并非一定缘于边坡稳定性降低，其位移时序曲线受库水位循环涨落及汛期降雨的影响，具有波动与震荡的特点。因此，只考虑单维度位移量的变化无法准确反映边坡稳定性的演化规律，而正确反映水库型堆积层边坡稳定性演化规律的位移信息应该是边坡位移与位移方向的多维度参数的综合反应信息，即：水库型堆积层边坡垂直位移与水平位移共同形成的位移矢量场的大小与方向变化规律决定了边坡稳定性的变化趋势。

综上所述，由于水库型堆积层边坡坡体的特殊物理力学性质及基岩面的限制，其位移矢量场的自由度为水平方向X和垂直方向Y两个方向，其稳定性是由位移矢量场的大小和方向两个因素共同决定，而传统位移量或位移速率只是描述位移矢量场大小变化的量化评价参数，根本反映不了边坡位移矢量场方向性的变化规律，其边坡位移量或位移速率的变化与突变并非一定预示着边坡稳定性的降低或失稳。边坡位移的变化只是其稳定性变化的必要条件，而非充要条件，其稳定性变化充要条件是边坡位移和位移方向的多维参数的综合变化。因此，本文根据“全息信息论”基本原理，在全面完整认识和确定滑坡位移量与多维度位移矢量场时空演化灾变机理与规律基础上，提出运用垂直位移方向率这一位移方向协调性参数，对水库型堆积层边坡稳定性进行全面完整地描述与评价，定义边坡垂直位移方向率为其位移矢量场的垂直位移量y与水平位移量x的比值η，即：

2.2 水库型堆积层边坡不同变形阶段其垂直位移方向率的演化规律假设边坡为各向同性的均质滑坡，其边坡基岩面倾角为θ（图1（a）），分别以平行与垂直边坡基岩面倾角方向作直角坐标系（X′-Y′），以水平与竖直方向作直角坐标系（X-Y）。在剪出口区域坡体上取任一单元体为研究对象，弹性变形过程中，假设单元体平行于倾角方向变化量（Δa），分解为X向分量（Δax），Y向分量（Δay）；垂直于倾角方向变化量（Δb），分解为X向分量（Δbx），Y向分量（Δby）。当边坡从弹性变形阶段转入塑性变形阶段，单元体应力将发生改变，不同位置会出现塑性区。此时单元体横向应变为，纵向应变为ε̇y，水位以下单元体有效主应力σ′（1水位以上单元体主应力σ）与X轴夹角记为α，2条滑移特征线分别记为β-和β+，其位移速率分量分别记为合成速率量分别记为（图1（b））。

图1 倾角为θ的均匀边坡坡体位移直角坐标

2.2.1 边坡弹性压缩变形阶段垂直位移方向率 根据弹塑性力学基本原理，边坡坡体任一单元体在弹性压缩变形阶段，其弹性体积应变不变，没有体积扩容，因此其变形前后的单元体体积不会变化，则：

其中ΔaΔb是高阶无穷小，可忽略，因此Δab=aΔb，设则有：

X方向的位移为：

Y方向的位移为：

边坡垂直位移方向率为：

由于滑坡倾角θ为一定值，且边坡在弹性变形阶段其k值也为一定值，k值大小与坡体材料性质有关，故该阶段其垂直位移方向率η为一定值，说明滑坡坡体任一单元体在弹性压缩变形阶段其垂直位移方向率不受其他条件影响，只与其倾角、坡体材料性质相关，具有很强的稳定性。

2.2.2 边坡塑性变形阶段垂直位移方向率 当边坡进入塑性变形阶段，根据塑性力学原理，其屈服函数为：

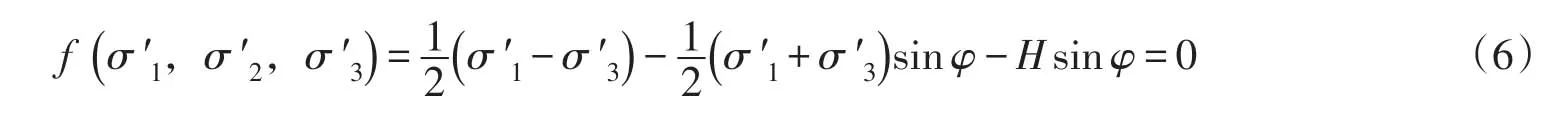
其中：σ1、σ2、σ3为主应力；H=c cotφ，c、φ为坡体黏聚力和内摩擦角。

将式（6）分别对σ′1、σ′2、σ′3求导，可得：

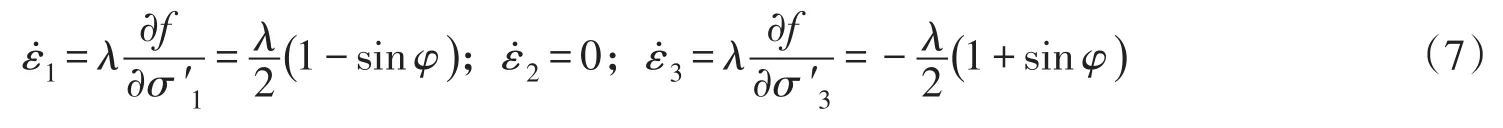
式中：ε1、ε2、ε3为主应变率；λ为比例系数，为一定值。

由式（7）可确定坡体的平均主应变率与最大剪应变率：

由式（8）、式（9）可得：

由式（10）可看出，当φ＞0时，坡体将会出现体积扩容。根据主应力轴与主位移速率轴相协调原则，可得：

令U、V分别为坡体沿X和Y方向的位移速率分量，其变形速率如下：

根据变形速率转换方程，可得：

根据式（15）、式（16），可知：

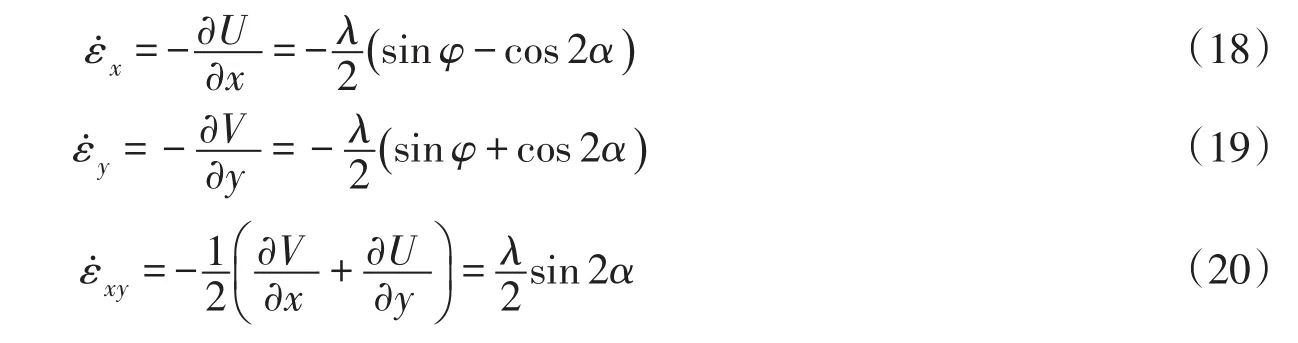
由坡体变形连续条件，可得塑性变形阶段边坡体积膨胀率为：

式中：为边坡体积膨胀率；γ为边坡纵向塑性变形率，

由式（18）、式（19），可求得边坡进入塑性变形阶段后其坡体垂直位移方向率：

2.2.3 边坡垂直位移方向率稳定性演化特征与规律 由式（21）、式（22）可得出以下结论：随着边坡坡体由压缩变形阶段进入塑性变形阶段，其坡体的应力不断发生变化与调整，当坡体的塑性区不断发展至贯通在一起而出现完整塑性区时，其此时其坡体体积膨胀率ḋ将趋近于无穷大，垂直位移方向率也将会发生突变。该式表明当坡体出现完整的塑性区时，定会引起垂直位移方向率参数的趋势性增大或减小，即在边坡挤压剪出口区域，γ＜0，其垂直位移方向率将呈现突变减小现象；在拉张松动区域，γ＞0，其垂直位移方向率将呈现突变增大现象（图2）。

图2 水库型堆积层滑坡不同滑移区示意

综上所述，剪出口形成区是滑坡岩土体达到塑性状态而产生压缩变形的滑移区，该区域内坡体表层的变形规律与坡体内任一点的变形规律一致。因此在剪出口形成区滑体整体剪出破坏前可通过监测该区域内边坡表层垂直位移方向率的变化规律判定边坡的稳定性阶段，即：当监测的边坡表层垂直位移方向率η为一定值或以某一定值为基准上下波动时，判定边坡处于弹性压缩变形阶段；当监测的边坡表层垂直位移方向率η逐渐增大或减小时，表明坡体塑性区不断发展，判定边坡处于塑性变形阶段；当监测的边坡表层垂直位移方向率出现明显突变时，表明坡体塑性破坏区已完全贯通，判定边坡进入整体滑移阶段。

3 水库型堆积层滑坡垂直位移方向率整体失稳判据的确定

由上述理论分析可知，当边坡处于弹性变形阶段，其剪出口形成区垂直位移方向率没有趋势性变化现象，而当边坡进入塑性阶段，塑性滑移区不断扩展至滑坡失稳前，其剪出口形成区垂直位移方向率会发生明显变化，该变化过程定会引起其垂直位移方向率的统计量γk发生趋势性移动。根据上述分析结果，能够运用数理统计趋势位移分析原理和数理统计特征参数来描述边坡剪出口形成区表层垂直位移方向率的变化规律与评价边坡稳定性，并以此建立边坡整体失稳的判据。具体分析方法如下。

假设边坡各监测点间互相独立，互不干扰，则同一边坡上不同监测点的垂直位移方向率变化遵循正态分布，且为具有相同方差σ2的随机序列η（ii=1，2，…，n）。其监测点垂直位移方向率的样本均值、方差及相邻方差分别根据下式确定：

根据统计学原理，当数据总体无移动时，S2与q2都为总体方差的无偏估计量，两值应该相近。而当总体发生逐渐移动时，q2因包含相邻两次观测之差而消除了大部分趋势性影响，而S2受到这种趋势性影响比较大。因此，为检验总体是否移动需求出边坡监测点k(k=1，2，3，…，m)上垂直位移方向率的统计量γk：

选用一定的置信水平α，可确定相应γk值的临界值其中为各监测点垂直位移方向率统计量平均值；为各监测点垂直位移方向率统计量方差；Zα2为标准正态分布的一个概率参数，α为置信水平，一般取0.05。利用实际监测数据算出γk及相应γd，然后对γk值进行检验。若边坡关键部位监测点γk≥γd，则判断边坡坡体没有出现趋势性位移；若γk＜γd，则判断该边坡坡体已发生趋势性位移。由于边坡趋势性位移的大小很大程度上预示着边坡的稳定性状态，因此可用整体趋势性位移率对边坡进行稳定性评价。

结合边坡剪出口形成区表层垂直位移方向率的演化规律，可认为：当K＜0，即γk≥γd时，判定边坡处于稳定变形阶段；当0＜K＜30%时，判定边坡处于不稳定变形阶段；当30%≤K＜100%时，判定边坡处于临滑阶段。

4 实例分析

4.1 新滩滑坡基本概况新滩滑坡位于长江三峡库区西陵峡上段出口北岸，1985年6月12日发生了体积约3000万m3的大规模滑坡[24]。由于相关部门对该滑坡进行了长期监测，预报准确及时，引起国内外地质学者的广泛关注。尽管该滑坡发生在三峡工程蓄水以前，但其汛期降雨引起地下水位及江水位变化诱发滑坡的失稳机理与受库水位循环涨落影响的水库型堆积层边坡极具相似性，且该滑坡具备稳定性演化全过程的监测数据，可为蓄水后类似水库型滑坡稳定性评价与监测预警提供重要借鉴。因此，本文以新滩滑坡为分析案例，研究水库型堆积层滑坡稳定性演化规律。

新滩滑坡位于新滩镇北岸，距三斗坪坝址27 km，滑坡长约2 km，近南北向展布，东西宽200～710 m，总面积约1.1 km2，平均坡度23°，后缘高程约900 m，边坡堆积物主要为崩积物、崩坡积物与崩坡积混合堆积物。边坡表部堆积物厚度为30～40 m，东薄西厚，西部厚度达86 m，其剖面图见图3[24]。

根据王尚庆[25]的研究，新滩滑坡稳定性演化可分为2个阶段：第1阶段为1983年雨季前，该边坡坡体变形处于由前缘向后缘分段递进式扩展阶段，具体可分为：1979年8月之前的蠕动变形期、1979年8月至1982年雨季的压缩变形期、1982年雨季后至1983年4月之间的变形发展期；第2阶段为整体推移式滑移阶段，具体分为：1983年5月—1985年5月的加剧变形期、1985年5月中旬—1985年6月12日的急剧变形期。

4.2 新滩滑坡监测点的垂直位移方向率及其稳定性演化规律新滩滑坡F系列监测点（F1—F8）位于该滑坡上段的姜家坡段，是边坡的不稳定主滑区。本文选取F系列监测点作为研究对象，统计并整理了1984年7月2日—1985年6月11日期间该系列监测点的水平位移与竖向位移数据（见表1）[24]，并求出上述时间段各监测点的垂直位移方向率（表2），绘制其垂直位移方向率随时间变化曲线图（图4）。

图3 新滩边坡上段剖面

表1 F1—F7观测点位移[25]（单位：m）

表2 F1—F7监测点垂直位移方向率

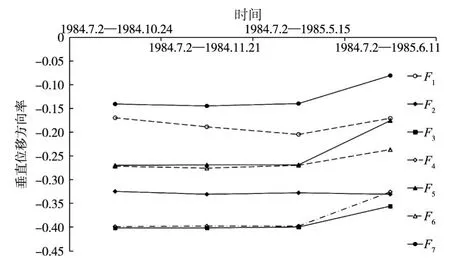
图4 F系列监测点垂直位移方向率随时间变化曲线

从图4可以看出，在1985年6月滑坡失稳前，F系列监测点的垂直位移方向率比较稳定，不随外力的变化而发生变化，表明该参数具有较强的抗干扰性，直到1985年6月滑坡发生失稳时，其值才发生突变。这与前面的理论分析相吻合。上述垂直位移方向率参数变化规律表明，该预测参数与边坡稳定性之间具有一一对应的关系，是一种有效的位移方向协调性参数。因此该预测参数对提高水库型堆积层滑坡的预测精度具有重要作用。

表3 F系列观测点垂直位移方向率判断结果（1984.7.2—1985.6.11）

4.3 边坡垂直位移方向率趋势位移判据的具体应用根据数理统计原理，对该边坡F系列监测点在1984年7月2日至1985年6月11日期间垂直位移方向率进行了统计分析与计算，得到了该时间段的垂直位移方向率趋势位移统计量γk与临界值置信水平取1-α=0.95，查表得Z0.025=2.4469）。通过对统计结果进行分析，分析结果见表3。

从表3可以明显看出，F1、F2没有出现趋势性位移，这与F1、F2观测点位于局部稳定区相吻合；而边坡上F系列其余监测点的垂直位移方向率在1985.6.11时已发生趋势性移动且趋势性位移率均大于30%，说明该边坡已处于整体滑移阶段，并即将失稳。该分析结果与该滑坡实际发生时间及滑移位置相吻合。上述规律表明可以运用垂直位移方向率参数及其趋势位移失稳判据对该类边坡进行稳定性评价与失稳预测。

5 结论

通过上述分析，可得出如下结论：（1）水库型堆积层边坡的位移矢量场由其水平和垂直位移矢量的大小与方向共同决定，而传统位移预测参数只能描述位移矢量场大小的变化，却无法反映边坡位移矢量场方向性的变化规律。因此，可运用垂直位移方向率这一位移方向协调性参数对该类滑坡的位移矢量场与稳定性进行全面完整地描述与评价。（2）水库型堆积层边坡垂直位移方向率预测参数与边坡稳定性状态存在一一对应关系，在弹性稳定压缩变形阶段，垂直位移方向率呈现相对稳定状态；在由弹性向塑性变形转化阶段，垂直位移方向率逐渐减小或增大；在边坡整体失稳前，垂直位移方向率将发生突变。由于位移参数在水动力作用下呈多级加速波动与突变，具有极其不稳定性，而垂直位移方向率参数具有显著抗干扰性与稳定性，因此，该参数克服了传统单维度位移量参数的局限性，具有位移预测参数不可替代的评价作用与意义。（3）根据数理统计趋势位移分析原理，建立了水库型堆积层边坡垂直位移方向率稳定性判据准则，即：当剪出口形成区垂直位移方向率统计量大于临界统计量时，表明边坡稳定；相反，则表明边坡不稳定，其中，若边坡整体趋势性位移率小于30%，则表明边坡处于不稳定阶段；若边坡整体趋势性位移率大于30%，则表明该边坡即将整体失稳。（4）本文以新滩滑坡为例，运用垂直位移方向率参数对该滑坡姜家坡段F系列监测点的实测位移进行了稳定性后验分析与评价，分析结果与该边坡实际稳定性演化阶段相吻合，表明垂直位移方向率参数是水库型堆积层滑坡有效的位移方向协调性评价参数，可运用该参数及其评价方法对水库型堆积层滑坡进行稳定性分析与评价。