空间柔性机械臂高阶滑模干扰观测器轨迹跟踪

杨 洋， 王思明

(兰州交通大学 电气与自动化工程学院，甘肃 兰州 730070)

0 引 言

考虑到太空环境的特殊性[1～3]，为了更有效地完成轨迹跟踪任务，本文采取二连杆的机械结构，针对机械臂抗干扰等问题进行控制研究。

于潇雁等人[4]主要采取了鲁棒控制，针对振动最优问题利用奇异摄动法将漂浮基二连杆机械臂系统分为快慢2个子系统并设计了状态观测器。王兴龙等人[5]研究了速度增益矩阵的动态调整方法,对二连杆机械臂进行MATLAB和ADAMS联合仿真，有效地抑制了系统的外界干扰及抖动。Muhammad Saad等人[6]运用非线性分离原则设计了机械臂基于级联高串联状态观测器，使用高增益参数有效地跟踪了非线性机械臂运动轨迹。Martino Capurso等人[7]运用卡尔曼预估器原理进行物理学建模，提出了一种无传感器的LTP方法并且已实际运用于现在冗余机械臂中，为轨迹跟踪问题提出了一种更为快速的方法。Hisashi Tamashima[8]主要针对双关节机械手轨迹跟踪问题提出了一种向量不同，阶级不同改进状态观测器。

以上诸多问题都是基于给定扰动的简单方程进行在线控制，而对于漂浮状态下的机械臂可能产生的复杂扰动方程并没有给出具体的控制方法，且上述先进算法计算量较大，极容易使操作者产生视觉生理疲劳，且需要具体研究对象的初始速度，以及需要实时监控数据，虽然实现了良好的跟踪效果，但是过程较为繁琐。

本文以漂浮基二连杆机械臂为研究对象，针对机械臂在漂浮状态中极易产生内部碰撞产生随机扰动的问题，利用高阶滑模算法设计了干扰观测器，首先利用拉格朗日方程对系统进行物理建模，结合对应的控制律以及跟踪轨迹方程对系统进行模拟仿真实验，最后将控制器运用于复杂方波轨迹中，实验结果表明，该方法不仅可以抑制系统产生的扰动，还可运用于更为复杂的轨迹中，有效地减少扰动精确跟踪期望轨迹。

1 二连杆机械臂建模

假设[9]:1)二连杆机械臂为钢体结构；2)空间忽略微重力对系统的影响；3)当系统在漂浮状态下，关节铰和关节轴均为钢体结构。

因此，建立的二连杆机械臂模型如图1所示。建立惯性坐标系∑I,基座坐标系∑O，关节坐标系∑i和末端执行器坐标系∑e，O为惯性坐标系的原点，C0为基座的质心，Ci(i=0，1，2)为连杆质心，Ji(i=0，1，2)为连杆i到连杆i+1的关节，CM为二连杆机械臂系统总质心，r0∈R2为基座质心位置矢量，ri∈R2(i=0，1，2)为连杆质心位置矢量，rc∈R2为质心位置矢量，re∈R2为末端执行器位置矢量，pi∈R2(i=0，1，2)为连杆位置矢量。

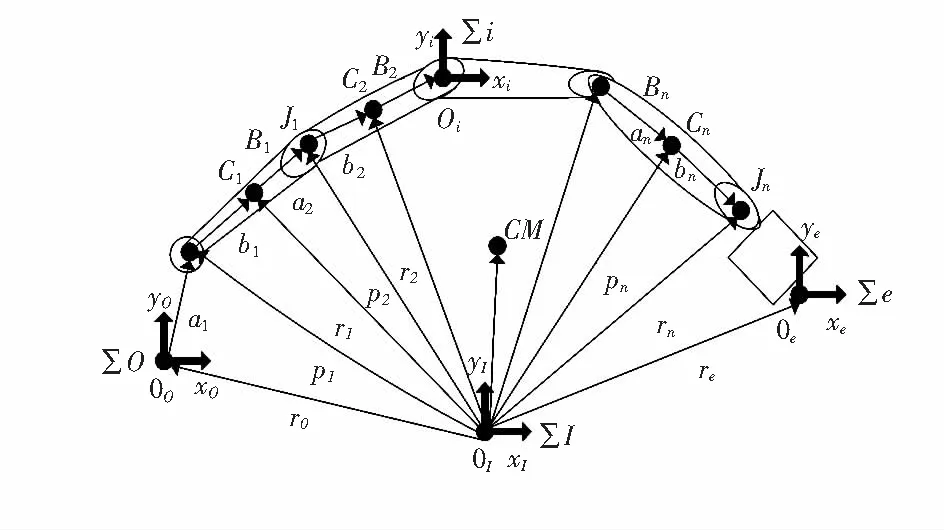
图1 二连杆空间机械臂平面结构模型

设机械臂各分部均在惯性坐标上运动，由于忽略微重力，系统动量守恒，固由Lagrange第二类方程可得漂浮下的机械臂系统运动学方程为

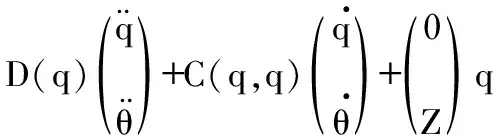
(1)

式中D(q)为系统7×7正定惯性矩阵，系统轨迹期望角q=[q0q1q2]T，系统角度补偿量θ=[θ11θ12θ21θ22]T,C(q,q)∈R7×7为系统所受哥式力，离心力7阶矩阵，非线性二连杆机械臂刚性矩阵为Z∈R6×6，系统电机驱动力矩矩阵为τ=[τ1τ2]T。

为了更方便地进行控制律设计，式(1)中所描述的系统具有以下几个定理：

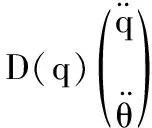
∀Ω∈R7×7

(2)

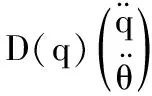
(3)

式中W0∈R7×7为关节变量回归矩阵，I1∈R1×7为系统驱动参数向量矩阵。

2 空间机械臂干扰观测器高阶滑模控制律设计

2.1 干扰观测器数学建模

根据上述对二连杆机械臂数学建模，将式(3)写成对角矩阵的形式，可得到

(4)

二连杆机械臂中电机的驱动方程为

RI1+L1+K2r-1=v(t)

(5)

式中v(t)为电机电压矢量，L和K分别为二关节不同电机驱动系数。将I1从式(4)代入到式(5)有

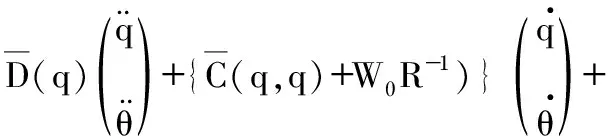
W0vR-1

(6)

此时，假设一个n维空间关节位姿向量p存在于惯性坐标系中，则p可表示为[10]

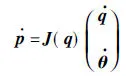
(7)

J(q)为Jacobian矩阵，对式(7)求导，可得

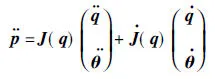
(8)

将式(7)、式(8)代入式(6)中，可得

(9)

为了使式(9)能够更直观地计算出基于此模型的干扰观测器数学模型，所以，对式(9)求逆矩阵，并写成状态输出矩阵为

(10)

求得系统输出u(t)得

u(t)=J-T(q)W0R-1v(t)

(11)

将观测器与系统实际输出相联系，求解观测器模型为

L(t)=(D-1(q)-I)u(t)-D-1(p+

C(q,)

(12)

2.2 高阶滑模控制律设计

基于上述观测器数学模型，定义x1=q,x2=， 将系统写成状态方程为

(13)

式中k为系统补偿矩阵，为了使得到的滑模控制律能使系统能观能控，假设：

假设1存在正定矩阵P，Q使矩阵K满足如下方程式

(Ai-BiKi)Pi+Pi(Ai-BiKi)=-Qi,i=1,2

(14)

假设2式(13)中补偿矩阵k满足

|ki|≤u(t),i=1,2

(15)

首先将系统控制律写成

(16)

定义

(17)

将式(12)、式(13)代入式(17)中，并对式(17)求导，得到

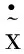
(18)

根据上式，首先定义滑模面为

Φ=x1-x1d

(19)

对滑模面求二阶导数

(20)

由式(20)可知，滑模面已出现控制量，为了更有效抑制扰动得到控制量，则对式(20)求出三阶导数，得

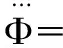
(21)

由式(21)可知，各个参数阶次相加，系统共6阶，而此方程中有关于驱动电机的电流、电压参数，这两个参数在实际运行中较为波动，不容易检测到，固本文在此基础上重新添加一个补偿正切函数，重新表示函数如下

(22)

(23)

式中λ1与λ2分别为对角矩阵，且‖λ1‖>‖λ2‖；系统在关节空间运行过程中，ε1与ε2都为7阶矩阵，且分别为两个电机驱动实时预估值。

得到预估值后，定义新的变量Γ1∈R7×7，Γ2∈R7×7，Γ3∈R7×7，将式(20)、式(21)重新表示为

(24)

本文研究的目的转化为式(24)的零点收敛问题，则可初步设置控制律为

(25)

式中f(t)为待设计阶矩阵，其通用公式一般写为

f(t)=-d1|Γ1|a1tanh(|Γ1|)-d2|Γ2|a2tanh(|Γ2|)-

d3|Γ3|a3tanh(Γ3|)

(26)

式中d1，d2，d3为3个7阶对角矩阵，并且满足Hurwitz多项式定理[11]，a1,a2,a3为3个参数满足

(27)

由于系统在运行过程中，不可避免地存在干扰，则在滑模函数一般形式上增加一个积分函数来抑制干扰，积分滑模函数为

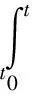
(28)

对式(24)所得的系统，重新分配参数设计控制器如下

(29)

2.3 系统稳定性证明

定义Lyapunov函数为[12]

V=1/2sTs

(30)

求导可得

(31)

将式(24)、式(26)、式(29)代入式(31)中，化简并将已知参数代入可得

=-sT{D-1(x1)·

(32)

由李雅普诺夫定理可知，系统在有效时间内收敛，固系统稳定性得证，此高阶滑模控制器可用于模型中。

3 高阶滑模干扰观测器仿真研究

在MATLAB中对图1进行模拟仿真实验，采用文献[13]的系统参数，式(12)观测器模型和式(29)的高阶滑模控制律进行编程仿真，具体参数体现如下：载体B0:m0=40 kg，L0=1.5 m，J0=34.17 kg·m2；刚性臂B1:m1=2 kg,L1=3.0 m，J1=1.50 kg·m2；刚性臂B2:m2=1 kg，L2=3.0 m，J2=0.75 kg·m2。控制器参数选择为

仿真过程中加入外界干扰和粘性摩擦为

F()=sgn()+k

(33)

设关节一和关节二的理想轨迹分别为：x1d=15×sin(0.2πt)，x2d=8×sin(0.6πt)仿真时间为10 s，仿真结果如图2所示。

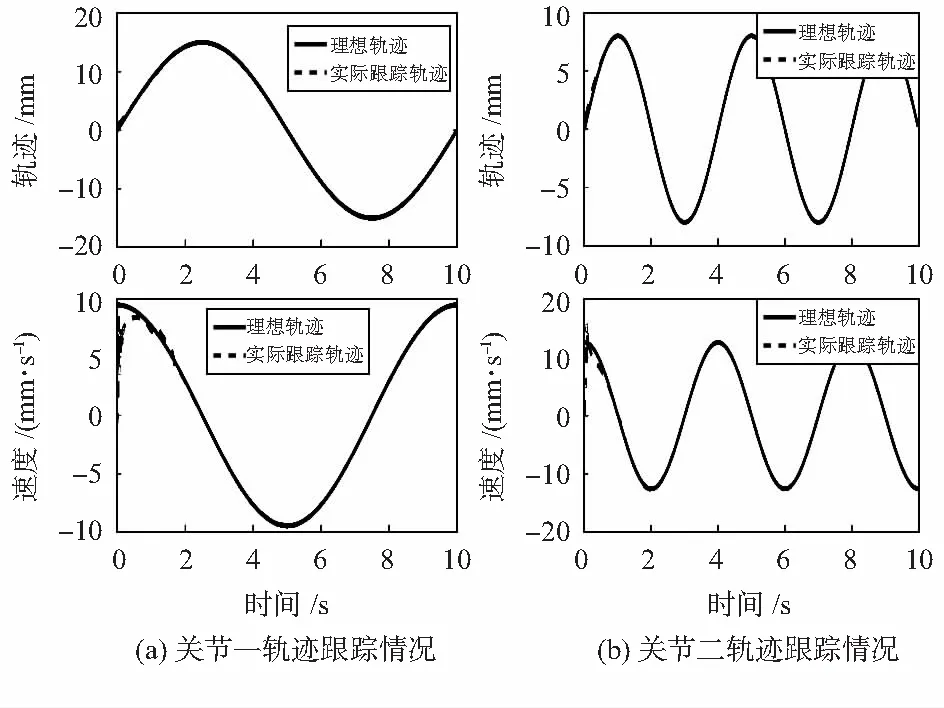
图2 仿真结果

图2(a)为关节一轨迹跟踪情况曲线，黑色实线为期望轨迹，红色虚线为系统实际运行曲线，下图为关节一速度跟踪曲线，图2(b)跟图2(a)类似，由于滑模算法本身具有抖动效果，所以,系统在刚运行过程中跟踪效果并不是很好，但关节一与关节二在大约1 s内逐渐跟踪上期望轨迹，并在接下来9 s的运行中，并未出现较为明显的抖动和误差，跟踪效果较为良好。

在关节一和关节二上的加摩擦力曲线，在干扰观测器的观测下，效果如图3所示。

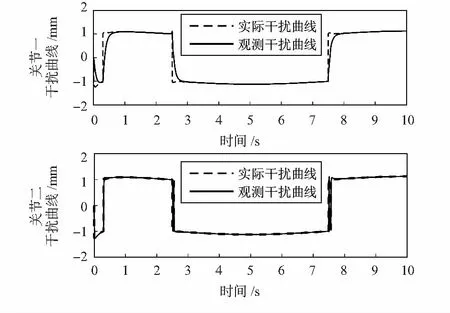
图3 关节一与关节二干扰观测效果

由图3可知，系统刚开始运行观测效果较不明显，但是关节一与关节二大约在1 s之后，观测器能精确观测到干扰曲线，而并未出现较为明显的误差。

为了更进一步证明此算法能运用于更为复杂的情况中，将机械臂理想曲线改为方波曲线进行进一步调试，结果表明，将此算法运用于方波轨迹中，系统在1 s后也与理想轨迹想重合，在后期工作中系统并为出现过大的波动。

4 结 论

实际仿真结果表明，在短时间内能够实现跟踪理想轨迹的任务，能够实时监控系统所受到的干扰摩擦等因素，不仅能够应用于正弦或者余弦曲线，亦能应用于方波曲线中。该研究对空间机械臂提供了一个新型的算法进行参考，同时也为该控制领域提供了一个新的方向。