基于变步长LMS和SVM的电能表内异物声音识别*
蒋晓永, 杨 涛
(1.西南科技大学 信息工程学院,四川 绵阳 621000; 2.特殊环境机器人技术四川省重点实验室,四川 绵阳 621000)
0 引 言
电能表异物检测的目的是检测电能表内部是否存在焊渣残留、松脂残留、脱落元器件、胶沫等异物或杂物。传统的人工电能表检测是按照一定的速度和旋转方向进行摇表听取声音判断电能表是否含有异物。检测效率低、检测结果不稳定。随着声学检测技术的日益成熟,通过声音信号的采集、处理和识别能实现对异物的检测。由于电能表内部异物的种类存在不确定性且存在较大背景噪声,增大了电能表异物检测算法的复杂性,需要研究噪声分离技术和基于学习的声音识别技术以提高检测的可靠性和准确性。
文献[1]提出心音信号的3种去噪方法,实验证明经验模态分解(empirical mode decomposition,EMD)去噪性能更好,但EMD降噪对于数据量较大时存在速度过慢以及模态混叠等问题;文献[2]针对脑电信号设计了误差归一化的最小均方(least mean square,LMS)自适应滤波器,效果良好;文献[3]提出语音增强中的3种去噪算法,得出了无偏归一化自适应去噪(unbiased normalization adaptive noise reduction,UNANR)性能较好,但收敛速度较慢。文献[4]将梅尔频率倒谱(Meier frequency cepstrum coefficient,MFCC)、差分MFCC以及短时能量3种特征用于高斯混合模型(Gaussian mixture model,GMM)的训练与识别,在处理不同环境的声音信号时,需根据实验结果确定GMM的参数,所以对GMM混合阶数的选择存在局限性;文献[5]提出了一种提取声音信号MFCC系数的方法和实验装置,解决了用HTK提取该系数的问题,采用非线性变换和离散余弦变换,优化了提取的MFCC系数,提高了语音识别的准确率。文献[6]提出了一种新的MFCC改进方法,通过对频谱噪声重构使改进后的MFCC系数具有良好的抗噪性。文献[7]提出基于MFCC参数和支持向量机(support vector machine,SVM)的心音信号识别,平均识别率达到了93 %,结果优于神经网络模型;文献[8]针对家庭环境训练数据不易获得的情况,采用SVM作为分类器,提取自适应MFCC参数作为特征,分类效果优于传统的分类器。
本文针对电能表内异物声音的特点并结合具体的应用背景,提出一种基于变步长LMS和SVM的电能表内的异物声音自动识别方法。针对SVM分类对噪声敏感的问题,先对采集到的声音信号进行数字降噪。然后提取声音信号的短时能量和改进MFCC系数组成混合特征矩阵并进行降维处理,并输入SVM分类器进行识别。
1 变步长LMS滤波算法
1.1 LMS基本原理
在车间采集声音时伴随着气泵、车床、风扇、电机等噪音,利用声卡一次采集2个通道的声音信号,一个通道放置有异物的电表,一个通道不放置电表作为参照。采用改进的变步长LMS自适应滤波降噪,将一个通道的信号作为输入信号,另一个通道的信号作为期望信号。自适应滤波器原理如图1。
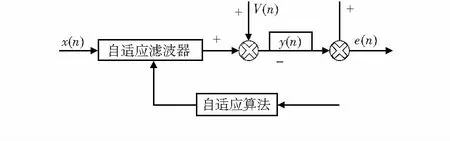
图1 自适应滤波器原理
其中x(n)为输入信号,y(n)为输出信号;v(n)为与x(n)不相关的信号,d(n)为期望信号,e(n)=d(n)-y(n),算法通过误差e(n)的值自动调整自适应滤波器的抽头权向量w(n),使得下一输出信号y(n+1)与期望信号更接近,从而使自适应滤波器逐渐收敛。基于最速下降法的LMS算法迭代公式为
y(n)=wH(n)x(n)
(1)
e(n)=d(n)-y(n)
(2)
W(n+1)=W(n)+2ue(n)x(n)
(3)
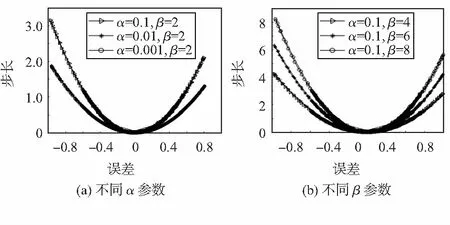
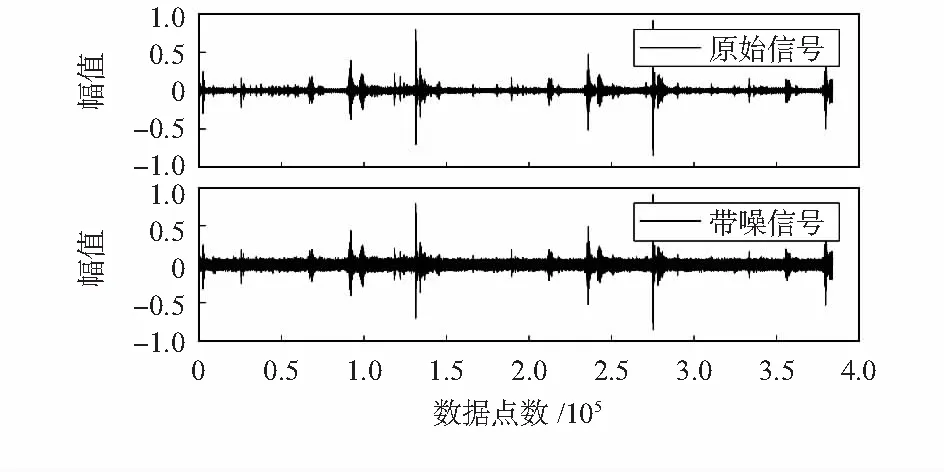
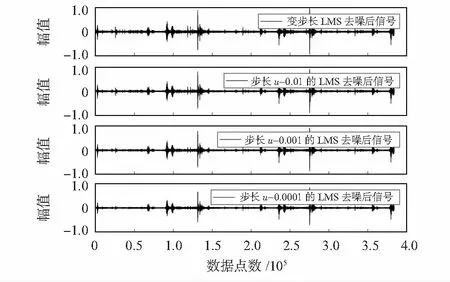
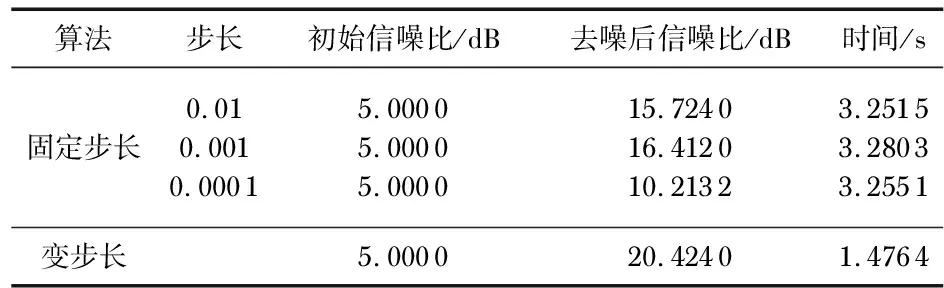
式中u为步长因子,通常为常数值,收敛范围为0 本文将步长同平方误差结合,建立新步长和误差之间的非线性关系。在一定程度上解决了收敛速度和稳态之间的矛盾且计算量小。改进后能够使步长在收敛稳时保持相对稳定,增大了适应性,新的步长因子为 u(n)=αu(n-1)+β(e(n))2 (4) 由式(4)可得到新的迭代公式为 W(n+1)=W(n)+2(αu(n-1)+β(e(n))2)· e(n)x(n) (5) 式中参数α控制步长变化函数的陡峭程度,β控制步长变化范围。步长与误差的关系如图2所示。开始收敛时,需要较大的步长加快收敛速度,而收敛稳态期需要较小的步长。在满足算法收敛的条件下,β的取值需要尽可能大。本文中设定a=0.1,β=9。 图2 不同参数下步长与误差的关系 1)声音的能量随时间而变化,预处理后计算第i帧声音信号xi(n)的短时能量E(i)为 (6) 2)通过Mel尺度频率域提取出MFCC具有较好的鲁棒性,能准确反映声音信号的特征。对每一帧信号进行快速傅里叶变换,将时域波形数据转换为频域能量信息并得到各帧信号的频谱。Mel滤波器的频域响应为Hm(k),通过滤波器后 (7) k=0,1,…,N-1 (8) 式中 参数N为声音信号x(n)的长度,C(k)为正交因子 计算得到MFCC参数 cos[πn(2m-1)/2M] (9) 引入差分系数来表现声音信号的动态特性。将动、静态特征结合起来才能更全面地反映声音信号的整体特征,能有效提高声音信号的识别率。计算帧间差分参数 (10) 式中dt为第t个一阶差分;Ct为第t个倒谱系数;Q为倒谱系数的阶数;K为一阶导数的时间差,可取1或2。 为了使得到的声音特征参数能全面反映声音信号的时、频特征,故对声音特征参数进行排列和处理。短时能量和改进MFCC系数构成混合特征矩阵,其第1维为短时能量,第2维第15维为MFCC系数。并对数据进行降维处理,求取混合特征矩阵最大特征值所对应的特征向量。将高维数据投影到较低维空间,在一定程度上减少声音特征矩阵的维度,为声音信号识别减少计算量。 检测电能表时不需要判别异物的具体类别,只需要判别电能表内是否含有异物。考虑到SVM可以较好地解决小样本、非线性、高维数等实际问题,在对声音信号进行降噪后提取特征识别,不仅可以解决SVM易受噪声影响的问题,还可以解决过拟合问题。 SVM可以将低维数据映射到高维空间,由支持向量来判决最优分割线,首先找出对分类有较好区分能力的向量,然后构造最大化类与类之间间隔的分类器,是一种由分离超平面定义的判别分类器。为了计算这个最优超平面,超平面定义如下 f(x)=α+βTx (11) 式中β为权重向量,α为偏置。通过对α和β缩放,可以尽可能多的获得最优化超平面 |α+βTx|=1 (12) 式中x为最接近超平面的训练集,被称为支持向量。使用式(13)得到点x到超平面(α,β)的距离 d=|α+βTx|/‖β‖ (13) 支持向量到超平面的距离定义为 d(s-v)=|α+βTx|/‖β‖=1/‖β‖ (14) 分类间隔为支持向量到超平面距离的2倍,即 M=2/‖β‖ (15) 对式(15)分类间隔M的最大化等价于在某些约束条件下的最小化。约束条件表达了对所有训练集正确分类的要求 (16) 式中yi为训练集的标签。 实验数据来源于工厂实际采集的电能表内异物声音信号(异物声音信号频率集中在3 000~4 000 Hz),选取一段较为纯净的异物声音,设定初始信噪比为SNR=5,叠加一定的随机噪声,原始信号与带噪信号如图3,原始信号与去噪后的信号如图4。 图3 原始信号与带噪信号 图4 原始信号与去噪后信号 2种算法都能一定程度地去除噪声,其去噪效果如表1。 表1 2种去噪算法的比较 由表1可知,固定步长LMS算法随着步长的减小,去噪后的信噪比先增大后减小,不同步长时的去噪效果差于变步长LMS算法,处理时间也明显大于变步长LMS算法。 采集到声音信号经过预处理和特征特提,得到一组代表声音信号特性的声音特征系数。但数据量大不利于快速计算,在实际生产中不能快速判断电能表有无异物。对数据进行降维处理,降低混合特征矩阵维度,减少声音信号识别的计算量。将混合特征矩阵和降维处理后的混合特征矩阵分别输入SVM分类器中进行识别,发现降维后虽然损失了一部分信息但有效提高了识别速率。具体表现为:信号数目分别为100,500,1000时,混合矩阵SVM识别时间分别为0.602 7,1.584 1,3.257 3 s,而降维后的SVM识别时间分别为0.203 5,0.792 1,1.293 1 s。 用本文提出的方法对电能表进行识别,实验采用留出法将数据集分为互斥的2部分分别作为训练集和测试集,经过重复实验1 000次得到的平均识别率在90 %左右。 本文对声音信号的数字降噪和识别进行了具体阐述,结合具体应用背景提出了一种新的变步长LMS算法,将误差和步长的关系建立了等式进行了讨论,最终得到一个适合于电能表内异物声音信号去噪的参数,但如何对采集的两个通道的声音进行对准以消除干扰有待进一步研究。提取声音信号的短时能量和改进MFCC系数组成混合特征矩阵,并对其进行降维处理,然后输入SVM分类器识别。该方法在一定程度上减小了计算量,提高了异物声音的识别率,有很好的应用价值。1.2 变步长LMS滤波
1.3 声音信号特征提取
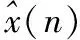
2 声音信号识别
3 实验验证
4 结束语

