结合多元曲线分辨与洛伦兹谱形约束的拉曼光谱分解算法

刘 薇 戴连奎

(浙江大学工业控制技术国家重点实验室，杭州 310027)

1 引 言

拉曼光谱检测技术具有测量周期短、灵敏度高、维护量小等优点，已越来越多地应用于在线检测[1～3]。随着拉曼光谱的广泛应用，相应的化学计量学方法也逐渐受到关注。由于混合物的拉曼光谱重叠峰严重，传统的多元统计分析方法常需要大量样本进行建模。在本研究组前期工作中，提出基于纯物质谱图对混合物拉曼光谱进行分解的方法[4,5]，提取目标物质的光谱信息，克服了重叠峰干扰，并解决了小样本情况下多元统计学分析方法预测不准确的缺点。

然而，上述基于纯物质的拉曼光谱解析法需要纯物质谱图，但通常难以无法直接获取所需要的纯物质光谱。因此上述基于纯物质的拉曼光谱分解法存在较大的局限性。

多元曲线分辨[6～8]基于谱图的线性叠加模型，是一类运用矩阵的线性分解处理多组分混合物信号，以解析纯组分变量的化学计量学方法。这种方法直接在混合物光谱矩阵的基础上，通过主成分提取(Principal component analysis，PCA)、渐进因子分析(Evolving factor analysis，EFA)[9]等因子分析方法分析混合物光谱矩阵中所包含的纯物质种类，并分离得到纯物质光谱矩阵及其对应的浓度变化信息。目前，多元曲线分辨主要用于从未知混合物的各种演进过程的数据中获得物质的变化情况，如高效液相色谱[10]、气相色谱[11]等联用色谱仪器和光谱滴定[12]、动力学光谱测定[13]等研究。

目前，混合物拉曼光谱矩阵不来源于某个渐进过程时，无法直接对其浓度变化情况进行分析。本研究提出结合多元曲线分辨与洛伦兹谱形约束的交替迭代最小二乘(Multivariate curves resolution-alternating least squares with lorentz constraint, MCR-LALS)拉曼光谱解析法，使用多元曲线分辨法分辨混合物各成分的拉曼光谱，并针对纯物质拉曼光谱满足洛伦兹曲线叠加[14,15]的特性，使用洛伦兹谱形约束的交替迭代最小二乘法进行谱形优化。本方法首先利用主成分分析将混合物光谱矩阵分解为得分矩阵与载荷矩阵的乘积; 在混合矩阵的样本光谱测量点方向上，利用渐进因子分析法分析不同测量点所包含的特征值，从而得到混合物中的纯物质成分个数及每个成分的谱峰范围，并初步计算各成分的纯物质谱图; 最后，采用基于洛伦兹谱形约束的交替迭代最小二乘法进一步优化各组分的拉曼光谱轮廓，此算法每次迭代过程中，首先对各组分光谱矩阵进行洛伦兹函数拟合，并结合非负性约束使用最小二乘法得到其系数矩阵，最后根据所得系数矩阵，使用非负最小二乘法得到对应的各组分光谱矩阵。当所得系数矩阵与各组分光谱矩阵乘积对初始混合物光谱矩阵拟合误差小于设定值时，迭代过程结束。将本方法应用于对二甲苯(PX)装置C8芳烃吸附塔循环液拉曼光谱分解，将分解结果与对应的纯物质光谱对比，为了进一步验证上述方法分解的有效性以及在小样本情况下的稳定性，将此分解方法用于对主要成分PX的定量分析，通过多次的小样本定量分析实验，并与偏最小二乘法(Partial least squares，PLS)的分析结果相比较。结果表明，在未知组分的情况下，基于多元曲线分辨的拉曼光谱分解技术可以实现对纯物质拉曼光谱的提取，并在小样本情况下可以进行准确稳定的分解。

2 算法介绍

本研究所提出的MCR-LALS分解算法基于以下矩阵方程[16]

DT=SCT+ET

(1)

其中，DT为已知的混合物样本的拉曼光谱，矩阵DT的维度为m×n, 其中n为混合物样本数，m为测量点数，在拉曼光谱中各测量点对应于不同的拉曼位移。在DT中，列向量为单个样本的拉曼光谱矢量，因此可以称之为样本光谱方向; 行向量表示在某个拉曼位移上各样本所对应的强度矢量，由于行向量包含各个样本的浓度信息，因此可以称之为样本浓度方向。S为分解得到的纯物质光谱的轮廓矩阵，其维度为m×p,p为后文分析得到的纯物质组分数目。CT为纯组分系数矩阵，其维度为p×n。ET为余差矩阵，其维度为m×n。算法的主要目的在于基于测量得到的DT矩阵，分辨出S和CT。主要分为以下几个步骤：

(1)对混合物光谱DT进行主成分分析，DT可以初步分解为：

DT=TPT+E=DT*+E

(2)

其中，T和PT分别为主成分分解得到的得分矩阵和载荷矩阵，也称为抽象光谱阵和抽象系数阵。

(2)进一步为了获得有物理意义的系数阵CT和光谱阵S，引入变换矩阵R:

DT*=TPT=TRR-1PT=SCT

(3)

则S=TR,CT=R-1PT。

使用EFA分析混合物中所含的成分数p, 对转换因子矩阵以及纯物质光谱阵S进行初步估计。在对液相色谱等渐进过程的研究中，EFA通常用于分辨渐进过程中不同物质的出现顺序及其浓度变化情况。EFA的分辨过程包括前向渐进因子分析(Forward evolving factor analysis, FEFA)及后向渐进因子分析(Backward evolving factor analysis, BEFA)两步[17]。沿着样本浓度方向，并利用化学物质依次出现的特性，FEFA首先对第一个样本谱图进行主成分分析求得特征值，再逐步渐进地延拓至整个矩阵，并根据上述FEFA分析结果将特征值对数对有序变量(如渐进过程的保留时间)作图得到特征值对数曲线，从而得到各成分的出现点; 而BEFA则从最后一个样本谱图开始进行主成分分析，再反向扩展到整个矩阵，BEFA将特征值对反向的保留时间作图，得到反向特征值对数曲线，从而得到各成分的消失点。同时，假设特征曲线图中首先出现的成分亦首先消失，因此可根据各成分在两种曲线共同存在的部分得到其浓度窗口，从而得到系数矩阵CT的初步估计。以此类推，假设待分辨的各成分拉曼谱峰沿着测量点也存在上述先出现亦先消失的顺序特性，因此本研究对矩阵DT在样本光谱方向上使用FEFA及BEFA，即沿着样本光谱方向，计算各测量点处DT子阵特征值并延拓至整个矩阵，再将FEFA与BEFA所得到的特征值对测量点及反向测量点作图，得到特征值对数曲线和反向特征值对数曲线，并根据两种曲线的共同存在部分得到各成分谱峰的出现顺序和谱峰存在的测量点范围。

根据上述分析结果，混合物中所包含的独立成分个数p等于最终得到的特征峰窗口数。对于各成分纯物质光谱，可根据其特征峰的存在范围，从光谱阵S中提取出该物质峰高为0的部分，结合步骤(1)分离得到的抽象光谱矩阵T，可得到符合要求的变化矩阵可行解R，从而实现对S的初步估计。

(3)上述EFA方法可以得到光谱矩阵S的初步估计。为了进一步完善其轮廓，得到具有物理意义的光谱矩阵，需要对矩阵S进行优化。本研究在交替迭代最小二乘优化算法的基础上，根据拉曼光谱的谱形特点，提出基于洛伦兹谱形约束的交替迭代最小二乘算法。根据文献[18]，交替迭代最小二乘法主要思路为结合EFA所得的结果作为S的初始值，并通过以下两式交替运算：

CT=S+DT*

(4)

S=DT*CT+

(5)

其中，S+及CT+分别为S和CT的广义逆矩阵。以上两式交替运算，直到SCT对DT*的拟合误差小于预设值，则优化过程结束。同时，在优化过程中需满足光谱及系数矩阵的非负性。

在拉曼光谱的分解中，假设混合物光谱检测过程仪器分辨率足够高，可以忽略光谱的高斯形变，因此拉曼光谱可以表示成k(k≥1)个洛伦兹峰的叠加和形式，在优化过程中，对纯物质光谱曲线可使用洛伦兹函数进行拟合及约束。设光谱阵S=[s1,s2,…，sp]，以其中一条纯物质光谱sj=(s1,j,s1,j,…,sm,j)T, (1≤j≤p)为例，则sj可以表示成

(6)

其中，L(φt,j)为洛伦兹峰的表达函数，φt,j=(at,j,wt,j,γt,j)为峰参数，分别为峰高at,j，峰的中心位置wt,j以及峰的半高宽γt,j;ej为拟合误差。

则基于洛伦兹谱形约束的优化目标及约束条件为：

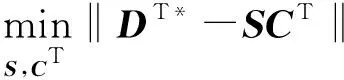
(7)

针对上述问题，基于洛伦兹谱形约束的交替迭代最小二乘算法的优化过程如下：

(1) 对矩阵S中的每一条纯物质进行洛伦兹函数拟合，并使用拟合结果代替S作为新一轮优化的初值; (2) 基于上述洛伦兹函数拟合光谱，使用非负最小二乘法得到其对应的浓度矩阵CT; (3) 使用更新得到的浓度矩阵CT，并利用非负最小二乘得到S; (4) 计算分解结果S×CT对DT*的拟合误差均方根，若其与DT*各元素的和的比值小于预设的拟合误差比例(此处设为1%)，则优化过程结束; 否则返回步骤(1)。

其中，步骤(1)中对纯物质光谱进行洛伦兹函数的拟合过程包括： Step 1设拟合光谱lj=0, 其对应的参数矩阵Φj=0; Step 2考虑光谱拟合余差sj-lj。首先寻找sj-lj的最大值a1,j，其位置w1,j以及半高宽γ1.j，将φ1,j=(a1,j,w1,j,γ1,j)加入到中Φj中，可以得到sj的第一个洛伦兹峰l1，j。lj=lj+l1,j; Step 3计算lj对sj的拟合误差均方根，若其与sj中各元素的和的比值小于预设的拟合误差比例(由于优化前期光谱偏差较大，此处设为10%)，则拟合过程结束。否则，继续寻找新的洛伦兹峰参数φc,j=(ac,j,wc,j,γc,j), 其中c表示当前参与拟合的洛伦兹谱峰个数，将其加入到Φj=中，则Φj=[φ1,j,…，φc,j]T。由于谱峰的加入，需要对Φj中的参数进行非线性最小二乘优化，优化目标式为：

(8)

3 实验部分

3.1 实验方法

本研究对PX装置吸附塔循环液拉曼光谱进行分解，并通过对其中的主要成分PX的浓度进行多次小样本的定量分析验证所提出方法的有效性。吸附分离法是生产PX的主要方法[5,19]，吸附塔循环液中除了PX外,还包括对二乙基苯(PDEB)、乙苯、间二甲苯等其它物质[20]。由于混合液中各成分拉曼谱峰相互重叠，同时现场测量得到的拉曼光谱易受到环境影响，从而降低了传统多元回归的准确性，也增加了曲线分解的难度。本研究使用自主开发的拉曼检测系统在线测量某炼油厂循环液拉曼谱图。系统框架如图1所示，包含现场采样装置与测量装置，中间利用光纤进行远距离通讯。现场采样柜为无电源本安结构，系统采用旁路式采样方式，利用工艺管线差压驱动，包括降温及过滤的功能。测量装置实现光谱在线测量，包括Laser785-5HFUO激光器(如海公司)、BAC100-785探头(美国BWTEK公司)、QE65000半导体制冷光谱仪(美国Ocean Optics公司)以及UNO-2174A工控机(研华公司)。同时对循环液进行手动采样，其成分浓度通过色谱方法测定，共得到25组样本。测量所得的原始谱图如图2所示。

图1 在线拉曼检测系统框架Fig.1 Framework of online Raman detecting system

3.2 光谱预处理

由于PX混合液的主要成分在波段680～880cm-1范围内均存在特征峰，文献[5,20]基于上述范围进行定量分析并得到了理想效果。另外，由于EFA分辨方法更加适用于光谱曲线局部分解，因此实验过程中选取特征680～880 cm-1进行分析。首先使用基于多项式滤波的方法去除基线[21]，同时将各混合物曲线分别除以其在680～880 cm-1波段内的最高峰值，以得到最大值归一化光谱，如图3所示。由于各样本光谱所含成分含量不同，因此归一化光谱中最高峰位置也不同。

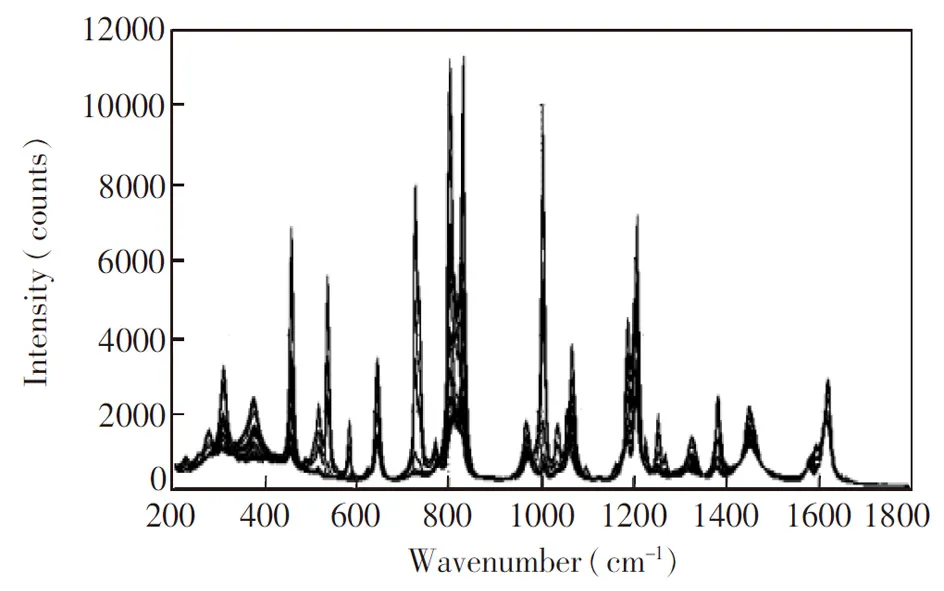
图2 循环液样本拉曼光谱原始谱图Fig.2 Original Raman spectra of circulating fluid samples

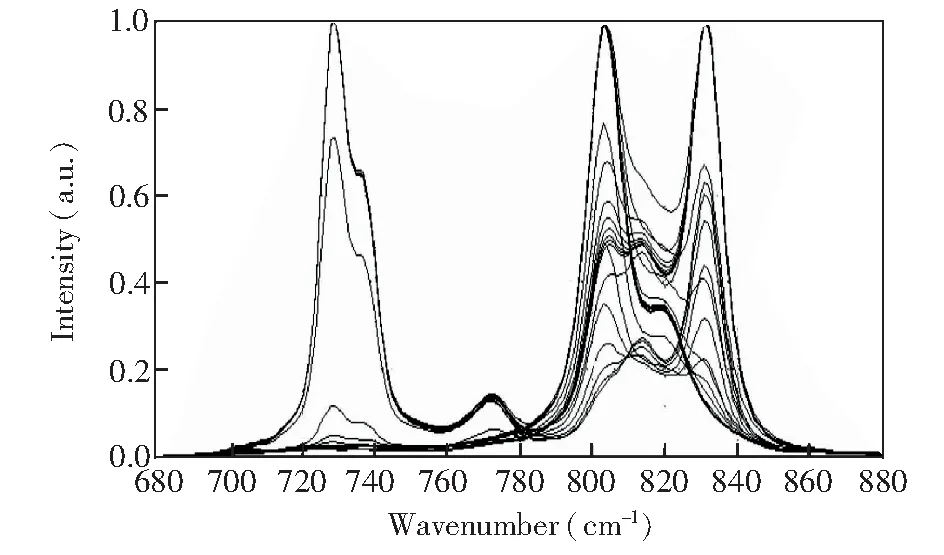
图3 全部样本经过预处理后的拉曼光谱Fig.3 Pretreated Raman spectra of all samples

4 结果与讨论

4.1 光谱分解

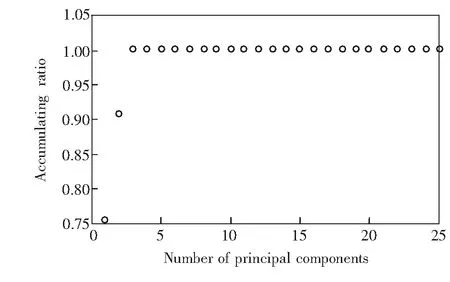
图4 各主成分特征值的累积比例Fig.4 Accumulating eigenvalue ratios for each principal component

使用EFA进一步分析光谱矩阵的成分个数，得到对应的特征值变化曲线(图5)，其中黑色实线表示FEFA特征值变化曲线，红色虚线表示BEFA特征值变化曲线。为了得到噪声特征值，结合图3中混合物光谱谱峰的起止范围(约为700～860 cm-1)，从图5中分别读取FEFA最大特征值对数曲线700 cm-1处的特征值对数(-1.99)以及BEFA最大特征值对数曲线860 cm-1处的特征值对数(-2.08)，计算上述两个数的均值得到噪声特征值约为-2.04。最终得到的有效EFA特征值变化曲线(图6，为了方便对比，将横坐标转换为其对应的波数)。其中，实线表示FEFA的特征值变化情况，虚线表示BEFA的特征值变化。如图6所示，EFA得到的独立成分共3组，与主成分分析所得到的初步分析结果吻合，其中 FEFA第一特征值与BEFA第三特征值组成第一个成分，谱峰窗口为700～777 cm-1; FEFA第二特征值与BEFA第二特征值组成第二个成分，谱峰窗口为725～830 cm-1; FEFA第三特征值与BEFA第一特征值组成第三个成分，谱峰窗口809～851 cm-1。

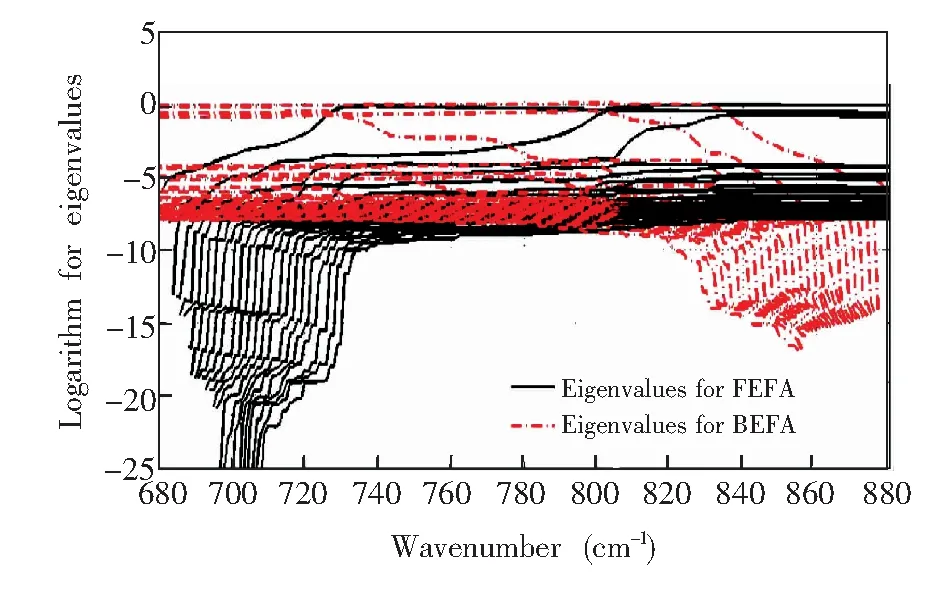
图5 前向渐进因子分析及后向渐进因子分析特征值对数变化曲线Fig.5 Logarithm lines for eigenvalues in forward evolving factor analysis (FEFA) and backward evolving factor analysis (BEFA)

图6 去掉噪声特征值后FEFA及BEFA特征值变化曲线Fig.6 Logarithm lines for eigenvalues with noise eigenvalues removal in FEFA and BEFA

图7 渐进因子分析得到的纯物质光谱曲线Fig.7 Pure spectra obtained from evolving factor analysis (EFA)

根据上述结果，可以将主成分分解得到的抽象矩阵分别截取前3个主成分的部分，转换矩阵R为3×3的方阵。为了进一步求取R，基于上述峰值窗口，分别提取出各成分峰值为0的部分，并结合T，可得到方阵R的一个可行解，从而得到纯物质光谱。对纯物质光谱进行最大值归一化，可初步得到各纯物质光谱，如图7所示。按照其峰值出现的顺序进行排列，共分离得到3条独立的纯物质谱图。

(9)

混合物及纯物质光谱的拟合误差随迭代次数变化曲线如图8所示，两种方法收敛速度相同，即纯物质光谱在约第15个循环周期时收敛到一个稳定值，而混合物光谱优化过程收敛速度更快，约第2个周期便得到稳定值，主要原因在于迭代过程中系数矩阵和纯物质光谱矩阵均是基于混合物光谱的最小二乘解，因此即使混合物光谱拟合误差收敛，由于纯物质光谱未必达到最优解，同样存在过拟合的可能; 而对比上述两种优化算法，ALS算法最终得到的混合物光谱更接近测量结果，LALS方法在谱形约束的条件下得到的纯物质光谱则更接近真实值，产生上述情况的主要原因在于测量噪声的影响。显然，LALS方法所得到的优化结果更有意义。

最终得到的LALS优化光谱如图9所示。图9还将分解得到的纯物质光谱与预先测量得到的混合物中各纯物质光谱相对比，#2纯物质光谱对应PDEB，#3纯物质光谱对应PX，而由于混合液中其它物质之间摩尔浓度的相关性较大，因此分解结果仅得到1条谱图。可以将其统一视为除PX及PDEB外的某种其它物质，对应#1光谱曲线，而此曲线为其它各物质光谱曲线的线性叠加。图9B显示原始纯物质谱图与分解谱图之间的误差，误差相对较大的部分出现在#1光谱中，主要由于其光谱在合成过程中存在偏差; 而多元曲线分辨方法区分PX与PDEB的纯物质光谱，其最大分解误差不超过0.05。在LALS优化过程中，主要对各纯物质光谱相互重叠的肩峰部分进行了谱形优化，从而减小分解误差，实现对两种物质重叠谱峰的充分分离。

图8 混合物(A)及纯物质(B)光谱矩阵拟合误差随不同优化方法迭代次数变化情况Fig.8 Change of lack of fitting (lof) for mixture spectra (A) and pure spectra (B) against the iteration times

图9 最终得到的纯物质谱图与实际纯物质谱图曲线 (A) 及其误差曲线(B)Fig.9 Comparison between pure spectra obtained by multivariate curves resolution (MCR) and the real spectra (A) and their residuals (B)

4.2 PX定量分析及方法对比

为了进一步验证上述分解方法的准确性，在上述分解结果的基础上，对循环液中PX摩尔浓度进行定量分析。由于拉曼光谱受测量环境及不同物质的拉曼效应强度系数的影响，其分解得到的系数矩阵不能直接表示物质浓度，因此本研究参考文献[5]，建立定量分析模型。模型校正及预测过程如下：首先对训练集矩阵进行光谱分解，然后通过训练样本中各组分含量以及分解得到的各组分系数矩阵求解混合物中各纯物质组分对应的拉曼效应强度系数。进行预测时，使用训练集分解得到的纯物质光谱矩阵对待测混合物光谱进行拟合，得到系数矩阵，并结合所得的拉曼效应强度系数求解PX摩尔浓度。

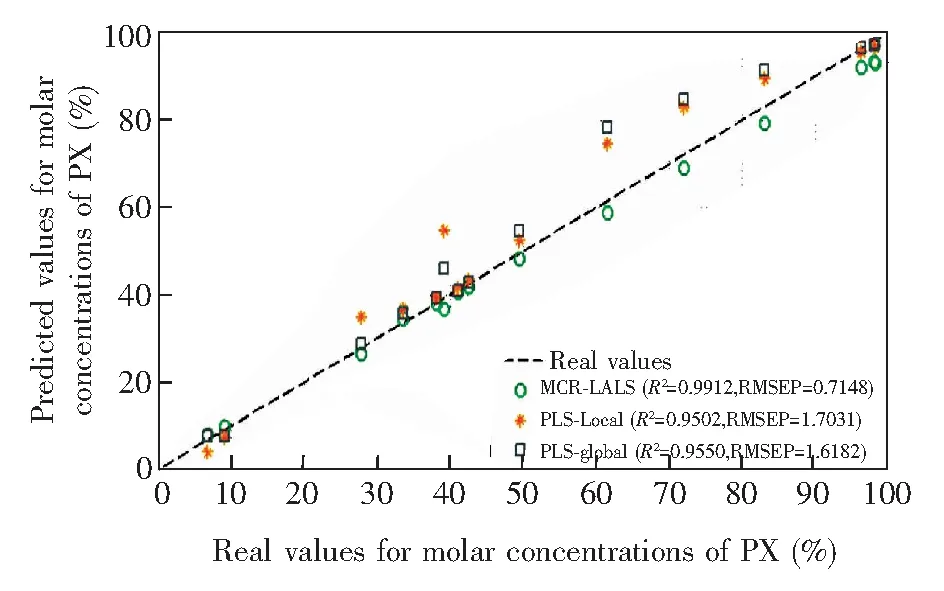
图10 预测样本数为10个时PX摩尔浓度的预测结果Fig.10 Prediction results of p-xylene (PX) molar concentrations by 3 methods when training number is 10

为了验证该分辨算法及预测模型的准确性，对比PLS进行定量分析，其中PLS作用范围分别选取全谱段1～2000 cm-1及680～880 cm-1特征谱段，选取主因子个数为3个。光谱经过最大值归一化及基线去除预处理。实验过程重复30次，每次从25个样本中分别随机抽取5个以及10个样本作为训练集，其它样本用于检验分析结果。算法的预测能力通过预测误差均方根(Root-mean-square-error of prediction, RMSEP)以及预测相关系数(Coefficient of determination,R2)进行评价。在其中一次实验中，当训练样本数为10个时，3种方法的预测值与真实值的对比结果如图10所示，样本中PX摩尔浓度分布跨度较大; 表1为多次实验所得到的综合评价结果,分别为3种方法分析结果的最大R2、最小R2、平均R2以及对应的最小RMSEP、最大RMSEP、平均RMSEP。由图10及表1可知，在小样本情况下，基于MCR-LALS的定量分析可以得到比较理想的结果，且相比于PLS模型，MCR-LALS随着样本数的变化，预测结果更加稳定。因此，在小样本的情况下，MCR-LALS依然能对混合物拉曼光谱进行有效的分解。

产生上述结果的主要原因在于，上述基于多元曲线分辨算法的定量分析模型原理与PLS等统计回归算法不同。统计回归算法假设待测组分含量与混合物光谱之间满足一定的线性关系。然而，在实际测量过程中，受激光器激发光强度、拉曼探头焦距与收集效率等外界环境的影响，即使测量同种物质，所得的拉曼光谱之间也存在偏差，而上述光谱重复性问题常导致谱图与待测组分含量之间的非线性关系，从而影响统计回归算法的准确性。同时，多元曲线分辨算法可分析得到各组分谱图及其加权系数，并基于所有组分的加权系数建立定量模型。在实际建模过程中，常基于各组分含量的相对比例及其归一化后的相对系数进行分析。在实际测量中，混合物光谱虽然随测量环境变化，但其所包含的各组分光谱加权系数之间相对关系保持不变，因此MCR-LALS模型并不受光谱重复性影响。此外，MCR-LALS分辨过程可有效克服测量噪声带来的影响，因此更具有鲁棒性。在实际工业现场测量过程中，由于无法保证测量环境的一致性以及所得光谱的重复性，因此基于多元曲线分辨的定量回归算法比传统统计回归算法更能得到稳定准确的预测效果。

表1 基于MCR-LALS定量分析与PLS模型预测结果对比

Table 1 Comparison of MCR quantitative analysis and PLS prediction results

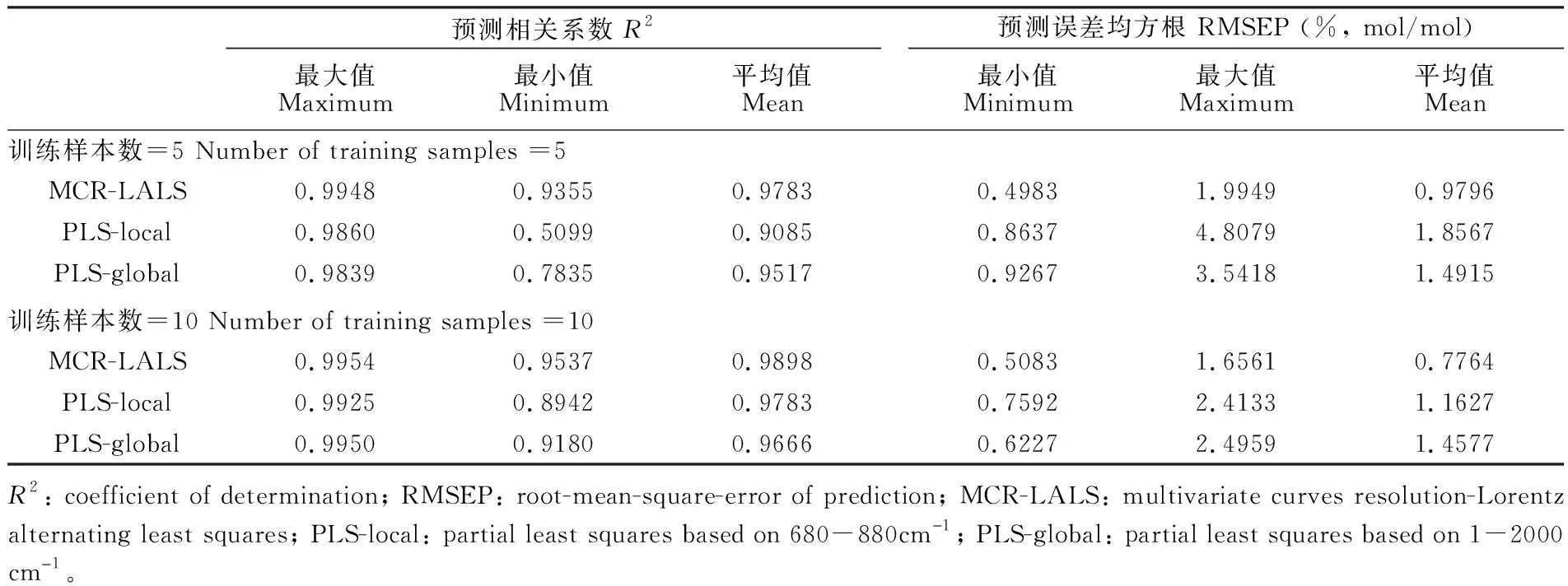
预测相关系数 R2最大值Maximum最小值Minimum平均值Mean预测误差均方根 RMSEP (%, mol/mol)最小值Minimum最大值Maximum平均值Mean训练样本数=5 Number of training samples =5MCR-LALS0.99480.93550.97830.49831.99490.9796PLS-local0.98600.50990.90850.86374.80791.8567PLS-global0.98390.78350.95170.92673.54181.4915训练样本数=10 Number of training samples =10MCR-LALS0.99540.95370.98980.50831.65610.7764PLS-local0.99250.89420.97830.75922.41331.1627PLS-global0.99500.91800.96660.62272.49591.4577R2: coefficient of determination; RMSEP: root-mean-square-error of prediction; MCR-LALS: multivariate curves resolution-Lorentz alternating least squares; PLS-local: partial least squares based on 680-880cm儊1; PLS-global: partial least squares based on 1-2000 cm儊1。

5 结 论

建立了结合多元曲线分辨与洛伦兹约束交替迭代最小二乘的拉曼光谱解析法。在实验过程中，使用本方法对PX装置吸附塔循环液的混合物光谱进行分解，得到其中独立的纯物质光谱。为了进一步验证此分解方法的有效性及其在小样本情况下的稳定性，对循环液主要成分PX进行多次小样本定量分析实验，同时使用PLS模型进行对比。结果表明，本方法可以分解得到准确的纯物质光谱，同时能够分辨各物质之间的重叠峰; 此外，在不同的样本数下仍然可以得到稳定且准确的分解结果，从而验证了本方法对混合物拉曼光谱分解的有效性。