反正切有限时间收敛微分器设计*

骆长鑫，张东洋，谭诗利，张 涛

（空军工程大学防空反导学院，西安 710051）

0 引言

高超声速飞行器是当今世界航空航天技术发展的新制高点，在未来国防装备发展和民用空天技术应用中将发挥着极其重要的战略作用。而微分信号的精确提取对高超声速飞行器的控制具有重要意义。当需要从受到噪声污染的信号中提取微分信号时，低通滤波器和微分传递函数等传统方法往往很难奏效[2]。我国韩京清研究员第一次提出了跟踪微分器（Tracking Differentiator，TD）的概念，并给出了几种具体的TD[3]。近些年来，国内外许多学者对TD的设计方法进行了深入研究，已提出了多种形式的TD[1，2-8]。尽管TD结构简单，并具备一定的噪声抑制能力，但无法证明估计误差有界[1-2，7]。现在的TD只能用于提取输入信号的有限阶导数（通常是一阶导数），而对于高阶微分信号的提取，尚未取得满意的结果。为获取输入信号的任意阶导数，以色列学者Levant提出一种高阶滑模微分器（High-order Sliding Mode Differentiator，HSMD）[9]。HSMD 在理论上可以提供输入信号的任意阶导数，但其设计参数选取异常困难，且对噪声十分敏感。所以，设计结构简单、具备一定噪声抑制能力并能够提供输入信号的任意阶导数的新型微分器势在必行[12-13]。

基于以上微分器研究现状分析，本文通过引入非线性函数设计了一种新型反正切有限时间收敛微分器（FD）。反正切函数可以保证FD收敛的快速性并能有效消除输出颤振。值得一提的是，所设计的FD简化了微分器设计参数，并能够提供输入信号的任意阶导数，具有传统微分跟踪器无法比拟的优越性。通过仿真验证了FD的改进效果及相对其他微分跟踪器的优势。

1 有限时间收敛系统设计

考察如下系统：

式中，a1，a2，…，an∈R+为待设计的参数，x1，x2，…，xn∈R为系统状态变量，fA（·）为连续函数且有fA（0，…，0）=0。

为了证明式（1）是有限时间收敛的，先根据文献[10]给出有限时间收敛的定义：

考虑下面时变系统

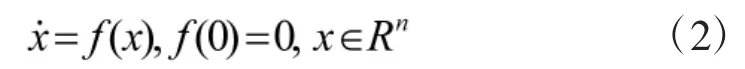
2）Lyapunov稳定：对于原点的任意一个开邻域Uε，存在一个包含原点的N的开子集Uδ，使得对和，有。

那么，式（2）的原点称为有限时间平衡点。

由定义知，对于式（1），若满足下列合理假设，则是有限时间收敛的。

假设1：式（1）是有限时间稳定的且停息时间函数Tf在原点连续，存在正定连续函数V0，使得0为实值并在N上连续，且有

假设2：存在一个Lipschitz的Lyapunov函数V0使式（3）成立，且其 Lipschitz常数为M0。

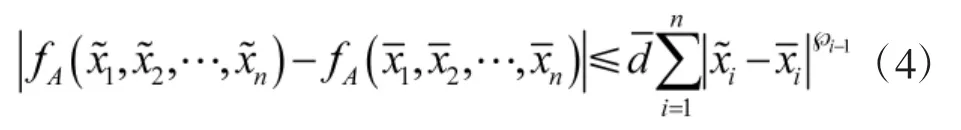
假设4：输入信号υ（t）分段连续可导，在整个时域内，υ（t）的前n-2阶导数存在，且允许在某些时刻tj（j=1，2，…，k），n-1阶不可导，但是其左导数与右导数均存在，并满足。

假设1～假设4的证明如下：

证明假设1：存在一个原点的开邻域Uε满足0＜x1＜x2＜…＜xn＜1。选取如下 Lyapunov函数

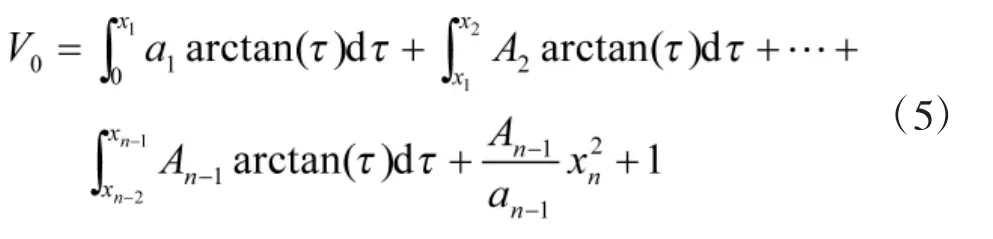
对V0求时间的一阶导数并代入式（2），有

注意到 0＜a1≤A2≤A3≤…≤An-1，an-1≤An-1，则式（6）变为

则式（7）变为

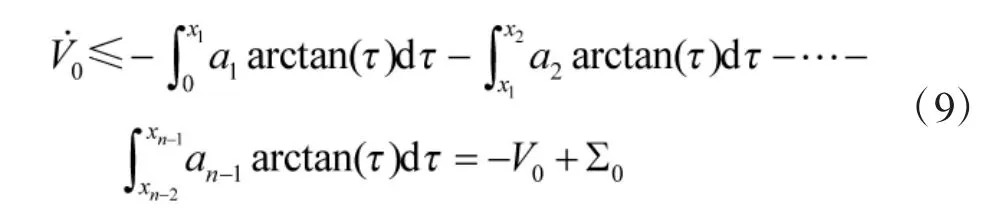
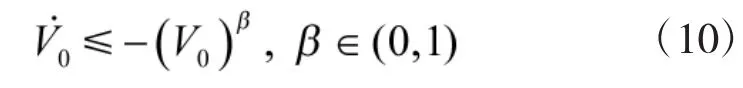
可见，假设1成立。证毕。

证明假设2与假设3：考虑到

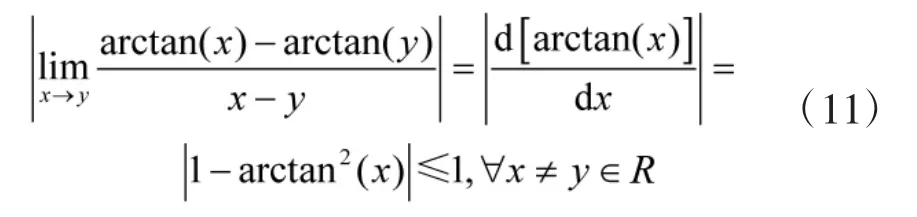
有

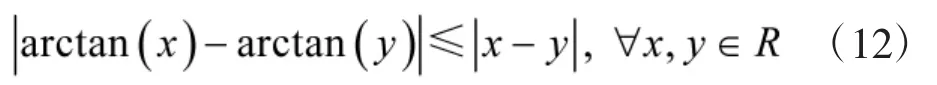
进一步，可得

可见，假设2与假设3也同样成立。证毕。

综上所述，式（1）是有限时间收敛的。

2 FD设计

FD的设计思路[10]：构造一个有限时间收敛式（1），通过等价变换，即可得到一种新型FD。

定理 1：如果式（1）满足假设 1～ 假设 3，υ（t）满足假设4，则得到如下新型FD

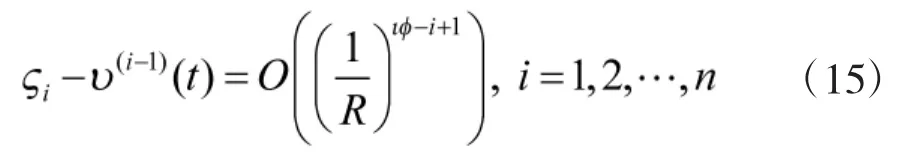
证明：根据文献[10]中的定理 1可知，式（14）成立。证毕。

特别地，传统 TD[2，6-8]只能对输入信号的一阶导数进行估计，本文提出的FD可估计输入信号的前n-1阶导数。

3 仿真分析

为验证设计的FD（仅以n=2的情形为例）的估计效果，分别将 FD 与下列新型TD[11]以及 HSMD[9]进行对比仿真。

仿真采用四阶Runge-Kutta法进行求解，仿真步长取为0.001 s。分别在以下两种情况下进行仿真。

仿真1：假设在高超声速飞行器控制中需要提取的信号为 υ（t）=sin（2πt）的微分，不考虑噪声影响，FD 的设计参数取为：R=600，a1=15，a2=0.005。

3种微分器对υ（t）及其微分值的估计效果如下页图1～图4所示。图2与图4表明，在3种微分器中，本文提出的 FD 对 υ（t）与（t）的估计误差最小，精度最高。由图4进一步可见，TD存在一个较为严重的峰值现象，HSMD在零点附近存在严重的抖振现象。因此，当不考虑噪声时，本文提出的FD较TD与HSMD均具有一定的优势。

仿真2：输入信号取为 υ（t）=sin（πt），并假设υ（t）受到随机噪声污染（见图5），FD 的设计参数取为：R=60，a1=0.2，a2=0.1。

由仿真结果（见图6～图9）可见，当输入信号υ（t）受到噪声污染时，本文提出的FD仍能实现对υ（t）与（t）的高精度、平滑估计。因此，与 TD 和HSMD相比，本文提出的FD在噪声抑制方面也具有一定的优势。

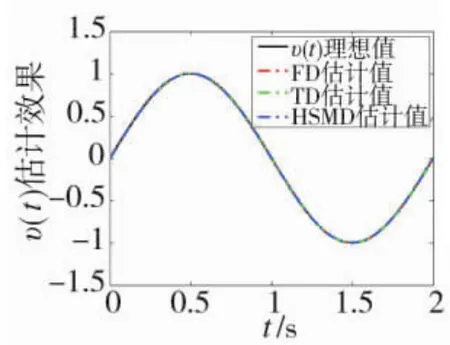
图1 v（t）估计效果

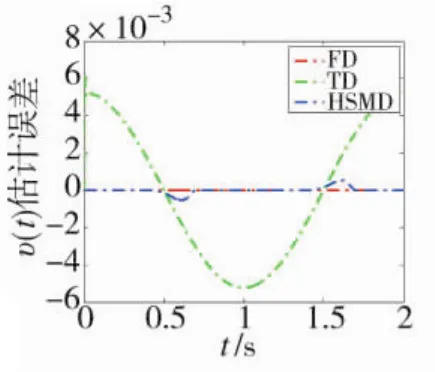
图2 v（t）估计误差

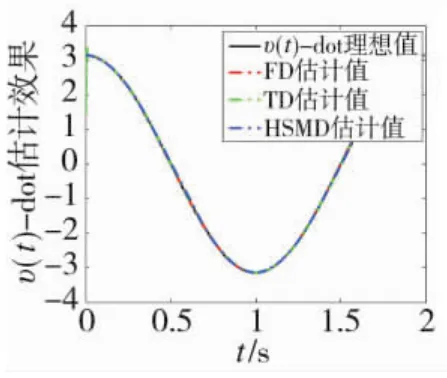
图3 （t）估计效果

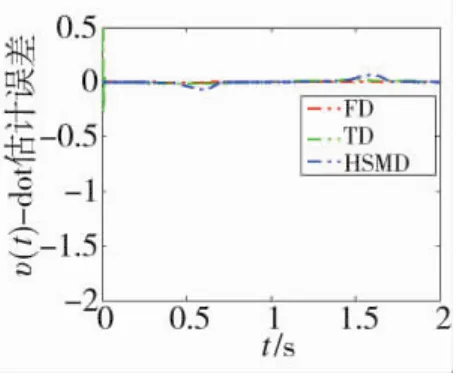
图4 （t）估计误差

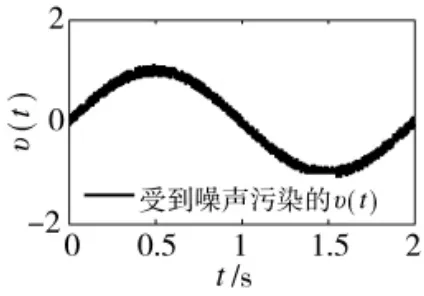
图5 受到噪声污染的v（t）

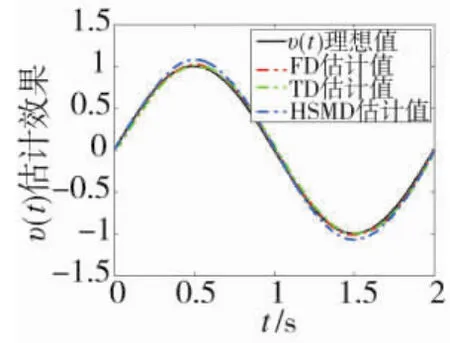
图6 受到噪声污染的v（t）估计效果

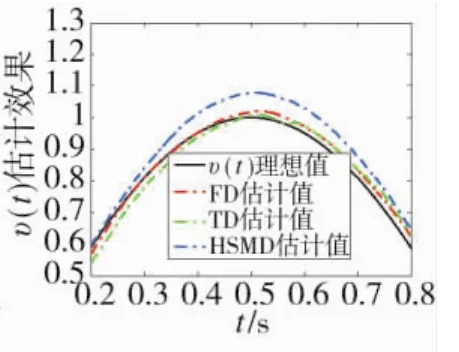
图7 v（t）估计效果局部放大

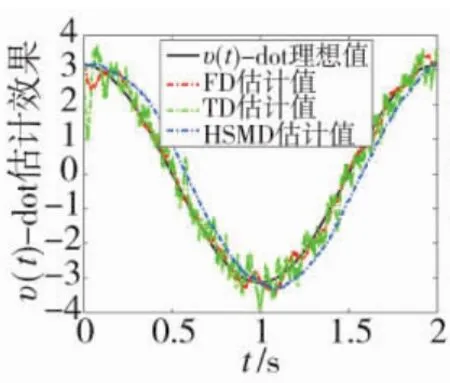
图8 受到噪声污染的（t）估计效果

图9 （t）估计效果局部放大

4 结论

本文基于反正切函数和终端吸引子函数设计了一种新型有限时间收敛微分器。仿真结果表明，FD不仅结构形式简单、设计参数相对较少，而且在跟踪精度、响应时间和滤波能力等方面较几种跟踪微分器均有一定的优势。