冲焊型液力变矩器叶轮辊铆工艺的研究

任工昌， 高 翔， 杨宇龙， 何 舟

(陕西科技大学 机电工程学院， 陕西 西安 710021)

0 引言

液力变矩器是一种以液压油为工作介质的非刚性扭矩变换器，具有良好的自动变速性能和过载保护性能，能够有效的消除动力传递中的冲击和震动，是液力传动的主要形式之一[1,2].液力变矩器主要由叶轮(涡轮、泵轮)、导轮、离合器等部分组成，根据叶轮的制造方法可以分为冲压焊接型液力变矩器(以下简称冲焊型液力变矩器)和铸造型液力变矩器.其中冲焊型液力变矩器与铸造型相比具有重量轻、密封性好、适合大批量生产等优势[3,4]，在现代汽车和工程机械领域被广泛使用.

辊铆加工主要用于冲焊型液力变矩器的生产制造，由于适用范围窄，国内的辊铆工艺理论尚不完善.现有的研究主要是将连接片的弯曲过程类比于一般的钣金折弯过程，参照钣金V型件的自由弯曲进行力学分析和计算[5-7].由于叶片的形状和弯曲方向并不规则，其辊铆过程与钣金弯曲过程具有较大差异，这种计算方法误差较大，加工中容易产生连接片根部鼓起和发生自接触变形等问题，导致连接片弯曲角度不足，与叶轮内/外环贴合不紧密，影响铆接效果.

本研究以某型号冲焊型液力变矩器涡轮叶片为研究对象，拟采用材料力学的基本理论对辊铆过程进行分析计算，并使用ABAQUS有限元分析软件进行仿真，通过对比仿真和实验的结果验证力学计算方法的可行性.解决了连接片弯曲角度不足，与叶轮内/外环贴合不紧密等问题，完善辊铆加工工艺理论，提高液力变矩器的生产效率，为辊铆机的设计计算和辊铆头的国产化提供理论依据.

1 辊铆过程分析

冲焊型液力变矩器叶轮的内环、外环以及叶片分别使用钢板冲压制造而成，然后再装配成完整的工作叶轮.叶轮的内环、外环及叶片的连接主要有焊接和铆接两种方式，与焊接相比，铆接连接变形小，不易产生疲劳破坏，对连接环境要求较低[8,9]，特别适合薄件连接.叶片与叶轮内/外环的连接属于典型的薄件连接，可以充分发挥铆接的优势，所以在叶轮的生产中主要通过辊铆加工进行铆接.

液力变矩器的涡轮叶片由叶片主体和若干连接片组成，涡轮叶片结构如图1所示.叶片的辊铆加工是指将叶片的连接片弯曲并与内/外环的表面紧密贴合，从而达到铆接的目的.加工效果要求连接片弯曲且方向和形状相同，与涡轮内/外环完全贴合，并要求间隙小于0.2mm.

图1 涡轮叶片结构

辊铆加工的过程主要分为插装定位、压弯及滚压三个阶段.在辊铆加工之前，首先要对叶片插装完成的涡轮进行定位，插装完成效果如图2所示.涡轮在辊铆过程中受力作用下，易在X、Y、Z轴方向上发生位移和回转，应以涡轮外环为定位基准，固定涡轮的六个自由度.

图2 叶片插装效果

预压弯阶段是指通过辊铆头的拨倒装置将插装完成的连接片从根部折弯，令其与涡轮内/外环的夹角小于等于30°.预压弯的目的是防止连接片的根部在滚压阶段鼓起，导致连接片发生自接触变形，从而影响铆接质量.

滚压阶段是指通过辊铆头上的滚轮对已经折弯的连接片进行滚压，令其进一步弯曲，减小连接片与涡轮内/外环表面的缝隙，使连接片与表面紧密贴合，保证叶片的铆接质量，辊铆加工效果如图3所示.

图3 辊铆完成效果

2 辊铆过程的力学计算

以某型号冲焊型液力变矩器的涡轮叶片为例，对叶片连接片的弯曲过程进行力学计算.已知叶片由厚度为1.2mm的08AL深冲钢板冲压而成，材料特性[10]如表1所示.

表1 叶片材料特性

2.1 压弯力的计算

Mmin=σmaxWz≥[σs]Wz

(1)

式(1)中：M/Nm—弯矩；Wz/mm3—抗弯截面系数；σs/MPa—叶片的屈服强度.

已知折弯处横截面为矩形

(2)

式(2)中：连接片宽度b=6.11 mm，连接片厚度h=1.20 mm(计算与测量结果取两位有效数字，下同).

由式(1)可得：

M=0.60 Nm

(3)

对连接片弯曲过程进行受力分析如图4所示.在图4中：Fs/N—拨倒装置的推力；Fn/N—连接片的支撑反力；θ/(°)—连接片的弯曲角度；连接片高度l=6.27 mm.

图4 压弯阶段受力分析

由图4可得：

(4)

Fs=Fncosθ+fsinθ=

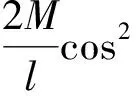
(5)

不计摩擦力，当θ=0时压弯力取得最大值Fsmax=192.25N.

2.2 滚压力的计算

图5 滚压阶段受力分析

忽略连接片根部变形对力臂长度的影响，可得：

(6)

则连接片顶端受到的滚铆力为：

(7)

连接片自重不计，当α=0时滚压力取得最大值Fvmax=99.92N.

3 连接片变形有限元分析与实验验证

3.1 连接片变形有限元分析

ABAQUS有限元分析软件致力于复杂和深入的工程问题，其强大的非线性分析功能在设计和研究的用户中得到了广泛的认可[11].在辊铆加工中，连接片的变形类型属于非线性变形，本研究拟采用ABAQUS软件对连接片变形过程进行模拟仿真，从而对上文的计算结果进行分析验证，ABAQUS非独立实体功能模块使用顺序[12]如图6所示.

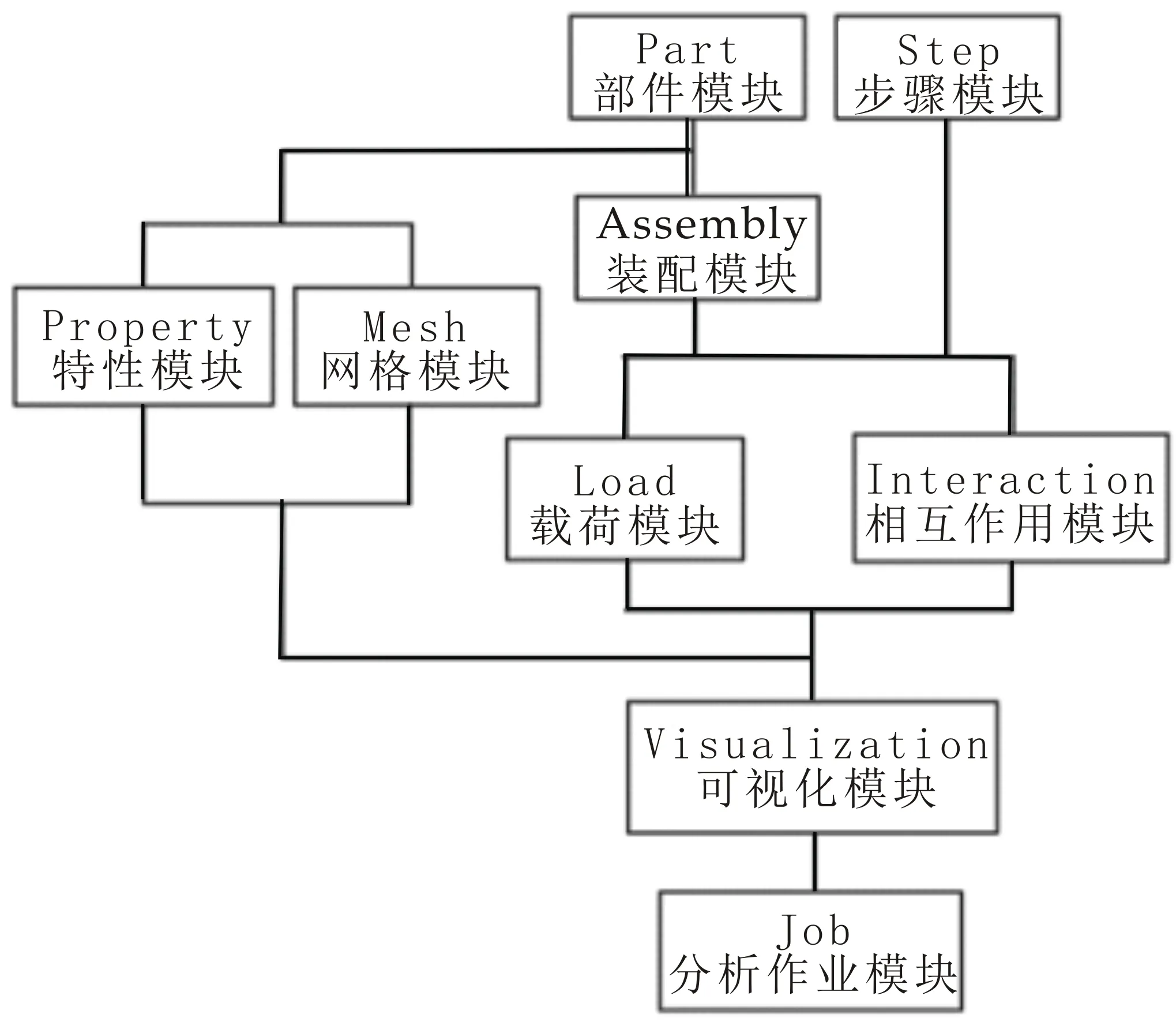
图6 模块使用顺序

3.1.1 ABAQUS有限元仿真

为了减小计算量和求解时间，本次仿真将叶片的其中一个连接片单独分离出来进行分析，用刚体平面代替涡轮内环.

首先，对连接片和刚体平面进行三维建模，使用SolidWorks软件对其进行三维建模，通过ABAQUS软件通讯接口导入模型并且进行装配.接下来，在Property功能模块中创建材料并分配截面，连接片材料性能如表1所示.本次分析对象为连接片，为了减少涡轮内环变形对分析结果的影响，将涡轮内环设置为离散刚体.在Mesh功能模块，对连接片和刚体平面进行网格划分，网格划分效果如图7所示.

图7 网格划分效果

连接片的变形分为两个阶段，因此建立两个General分析步，Step1进行预压弯阶段的分析，Step2进行滚压阶段的分析.由于以上两个阶段连接片的变形都是塑性大变形，因此选择迭代求解器，开启Nlgeom(几何非线性)选项.选择convert severe discontinuity iterations(转换严重不连续的迭代)选项，防止网格过度变形引起的迭代不收敛的问题.

分析辊铆过程可知，连接片所受的载荷是移动变载荷，其大小随作用点位置变化，并且载荷的施加位置也随时间变化.ABAQUS / Standard为用户提供了大量的用户子程序，能够使ABAQUS适应其特定的分析需求.当负载是时间和/或位置的复杂函数时，通常使用ABAQUS用户子程序DLOAD[13-15].本次模拟使用FORTRAN语言编写子程序代码，并通过DLOAD子程序接口定义载荷，部分代码如下.

…

SUBROUTINE DLOAD(F,KSTEP,KINC,TIME,NOEL,NPT,

1 LAYER,KSPT,COORDS,JLTYP,SNAME)

C

INCLUDE ‘ABA_PARAM.INC’

C

DIMENSION TIME(2),COORDS(3)

CHARACTER*80 SNAME

PARAMETER(P0=192.25,Dm0=6.27,Dmiu=0.002,speed=1,width=0.2)

Pi=3.14

Disp=TIME(1)*speed

CONST=COORDS(2)/(0.31+Disp)

xMin=Disp+0.002

xMax=Disp+width-0.002

IF(COORDS(2).ge.xMin.and.COORDS(2).lt. xMax)THEN

F=P0*CONST*CONST

ELSE

F=0

END IF

…

接下来设置边界条件，选择ENCASTRE选项将连接片的底部和刚体平面完全固定，然后建立接触，定义连接片的弯曲面与刚体的上表面为Surface-to-surface contact接触，其中刚体的上表面为主面，连接片为从面.不计摩擦力，将切向属性设置为Frictionless，采用小滑移计算公式，数据检查无误后提交作业.

3.1.2 仿真结果分析

进入Visualization模块，查看分析结果，两个分析步的等效塑性应变结果如图8所示.为了更加直观的分析连接片的受力变形过程，在连接片内侧顶部建立了参考点，通过其竖直方向的位移来体现连接片的变形程度.

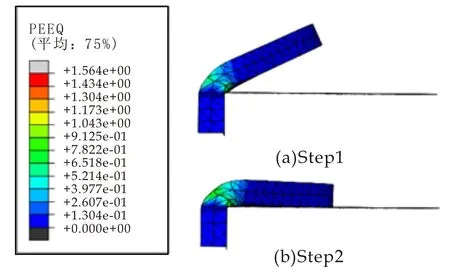
图8 等效塑性应变云图

在Result模块中输出ODB场变量，并在Origin中绘制了参考点的位移与载荷的变化曲线，参考点位移与载荷变化趋势如图9所示.从图9可以看出，压弯力和滚压力的数值和变化趋势与计算结果相符，其中预压弯阶段和滚压阶段参考点的竖直位移分别为3.18 mm和3.09 mm，压弯力和滚压力的峰值分别为192.25 N和99.2 N.

(a) step1

(b) step2图9 位移-载荷曲线图

使用Query选项中的Angle和Distance工具对仿真结果进行测量，测量结果如表2所示.连接片的弯曲角度和与涡轮内环的间隙均满足加工要求.

表2 测量结果

3.2 验证实验

使用ABAQUS软件对连接片的变形过程进行模拟仿真，可以预见连接片的变形过程和结果，初步验证了力学计算方法的可行性.零件在实际加工中的工况比较复杂，影响加工效果的因素很多，模拟仿真存在一定的局限性，因此接下来对叶轮的辊铆过程进行实验验证.

影响连接片铆接效果的工艺参数主要有拨倒力、滚压力、保压时间等，本研究借助陕西某企业的P-802753型辊铆机对上述叶轮进行实验验证，部分工艺参数如表3所示.

表3 工艺参数

本次实验随机选取了十二个叶片插装完成后的液力变矩器的涡轮，对涡轮的内环进行了辊铆加工，铆接效果如图10所示.

图10 实验结果细节

在每个加工完成的涡轮内环上随机选取了一个连接片进行测量，使用式(8)计算出了涡轮内环与连接片的间隙，计算结果如表4所示.

S=m-(h+n)

(8)

式(8)中：S/mm—间隙，m/mm—涡轮内环与连接片的总厚度，n/mm—涡轮叶片厚度，h同上.

表4 计算结果

分析实验结果，去掉最大值0.20和最小值0.05，可得：

另外，还可由表2知，ABAQUS软件的仿真结果，连接片与涡轮内环的间隙

实验结果与仿真结果虽然略有差别，但仍然满足加工要求.考虑到仿真过程中忽略了涡轮内环的变形等因素，误差仍在可接受范围之内，进一步验证了辊铆力学计算方法的正确性及有效性.

4 结论

本文根据冲焊型液力变矩器的叶轮结构和加工工况，分析了叶轮的辊铆加工过程.针对当前生产中存在的连接片弯曲角度不足，与叶轮内/外环贴合不紧密等问题，改进了辊铆加工中压弯力和滚压力的计算方法并通过ABAQUS软件对连接片的变形过程进行了仿真，通过对比仿真和实验的结果验证了计算方法的可行性.

本研究以某型号冲焊型液力变矩器为研究对象，对连接片及涡轮内环进行了适当的简化，忽略了加工中的摩擦力，未考虑涡轮在加工中存在的弹性变形等问题，具有一定的局限性.液力变矩器的叶片形状多种多样，应当具体问题具体分析.