排叉结琼斯多项式根的分布

韩友发，孙思宇，孙艺丹，王英姣

纽结理论是低维流形的重要研究领域，而且得到了广泛应用.分类是纽结理论的重要课题，而环链多项式扮演了重要角色，从早期的Alexander［1］结多项式，到近代的纽结琼斯多项式［2-5］，都极大促进了该领域的发展.国内外专家对此进行了深入研究，为了探讨整系数多项式与纽结多项式的关系，人们对纽结琼斯多项式的零点分布产生了相当浓厚的兴趣.在文献［6］中，Wu和Wang研究了链环和纽结的Jones多项式的零点的性质.他们给出了重复链环和环面结的Jones多项式的根的性质，同时又计算了某些纽结族的Jones多项式，并给出了其根的性质.在文献［7］中，Chang和Shrock讨论了四类对应图的交错链环类的Jones多项式，并给出了它们的零点.在文献［8］中，Xi’an Jin和Fuji Zhang给出了纽结和链环的Jones多项式在整个复平面内零点分布性质，讨论了某些排叉链环和某些基于DCn（每条边都是2-重边的n-圈）的纽结多项式的零点的性质［9］.在文献［9］中，研究了排叉结p(c1,c2,c3)与排叉结p(k ,k,k)的Jones多项式的零点性质，在文献［10］中，讨论了排叉结的Jones多项式及其零点分布，计算出排叉结 p(k ,k,l)的多项式，然后利用相同的方法讨论排叉结 p(k , k,l)的Jones多项式的零点分布.

本篇论文包含二部分，第一部分给出了链环和纽结的概念，琼斯多项式的基本性质以及排叉结的基本性质；第二部分研究了排叉结p(k ,k,l)的Jones多项式及其零点分布.

1 预备知识

1.1 纽结的基本性质

定义1 把嵌入到三维球面S3或者欧氏空间R3中的单位圆周S1称为纽结；若给纽结一个定向，则得到有向结.

1.2 纽结的多项式

引理1［4］对任意一个有向投影图L都对应一个关于t的整数系数多项式V(L )，满足下面三个条件：

（1）同痕不变量.若有向投影图L与L′互相同痕，则它们所对应的多项式相同，即：V(L)=V(L′)；

对于琼斯多项式的其它定义，可参见文献［1-5］.

1.3 排叉结

定义3 排叉链环p(c1,c2,…,cn)是由n元数组(c1,c2,…,cn)确定的，其中ci≠0，i=1,2,…,n，n≥3，| ci|表示该处上的半扭转数，ci的符号代表扭转数的正负号.排叉结标准图如图1所示.

图1 排叉结

引理2［3］（I）（1）如果所有的ci都是奇数，那么①当n为奇数时，p(c1,c2,…,cn)为纽结；②当n为偶数时,p(c1,c2,…,cn)是两个分支的链环.

（2）若存在一些ci为偶数，则偶数的ci的个数就与链环p(c1,c2,…,cn)的分支数相同.

（II）若所有ci的符号都一样（即都为正或都为负），那么 p(c1,c2,…,cn)为交错链环.

（1）如果 ci＞0，那么 A区域的个数

（2）如果 ci＜0，那么 A区域的个数 a͂=n，B区域的个数

关于A区域和B区域的介绍可见文献［3-4］.

定义4 排叉结的定向：p(c1,c2,…,cn)的一半边上标有αi，i=1,2,…,n，所有αi的符号决定了排叉结 p(c1,c2,…,cn)的定向.即左定向←（右定向→）将赋值-1（+1）给αi.

p(c1,c2,…,cn)的定向如图2所示.

图2 p(c 1 ,c2,…,cn)的定向

引理3［3］任意带定向的排叉结或排叉链环的拧数为

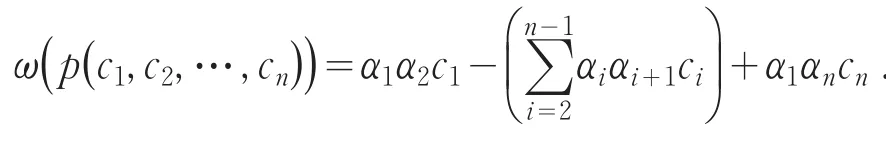
接下来研究ci＞0的排叉结 p(c1,c2,…,cn).

引理4［7］假设链环L的连通交错可定向的投影图D，D具有个 A区域，个B区域和拧数ω.那么链环L的Jones多项式由投影图D的联合图G的图特多项式给出：

引理 5［10］

2 排叉结的琼斯多项式与其零点分布

定理1 排叉链环p(k , k,l)（其中k为正数）的琼斯多项式：

当 k为奇数，l为奇数时，则VL(t)=

当k为奇数，l为偶数时，则VL(t)(α1=+1,α2=-1,α3=+1) ；

当 k为偶数，l为奇数时，则VL(t)=(α1=+1,α2=-1,α3=+1) ；

当 k为偶数，l为偶数时，则VL(t)=(α1=+1,α2=-1,α3=+1).

证明 由引理3可得w(p (k ,k,l) )=α1α2c1-，再由引理4和引理5可得：当k为奇数，l为奇数时，

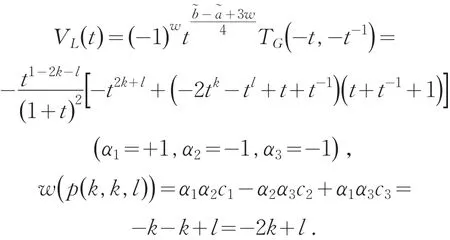
当k为奇数，l为偶数时，

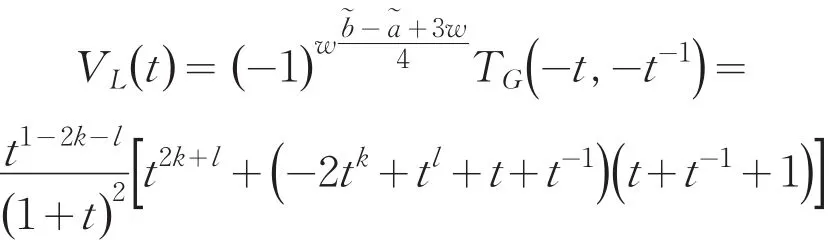
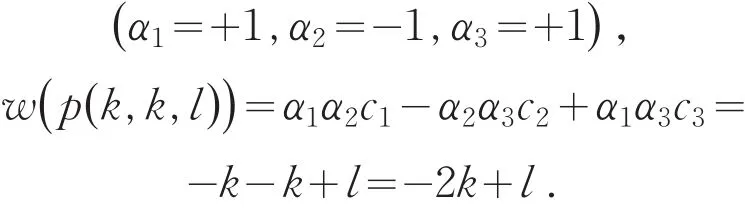
当k为偶数，l为奇数时，

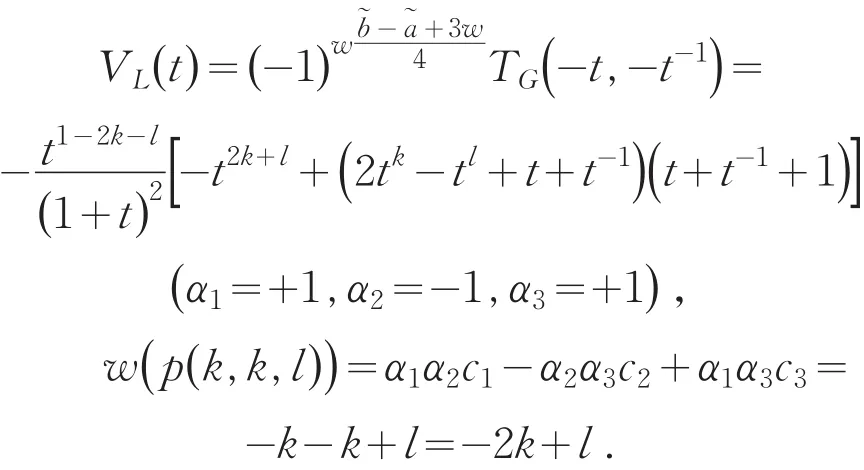
当k为偶数，l为偶数时，

定理2 当k固定，l→∞时，排叉链环p(k ,k,l)（其中k为正数）的Jones多项式的零点分布在曲线-t2k=t+t-1+1上.

证明 令上面定理中的Jones多项式等于零，得到

对上述四个式子，当k固定，l→∞时，得到结论.

3 结论

本文利用链环投影图的区域数、拧数和图特多项式给出排叉链环p(k ,k,l)琼斯多项式的一种表示，根据这种表示讨论多项式根的分布性质，给出了非温良结琼斯多形式根分布的曲线，给出这方面研究是一种尝试.