定数截尾情形下三参数Weibull-Poisson分布的Bayes估计
2019-01-11 08:56:20李晶
通化师范学院学报 2019年2期
李 晶
三参数Weibull-Poisson分布是王蓉华[1]等定义的一种新的寿命分布.在寿命试验中,由于受到各种外界因素的影响,得到完全样本的难度比较大,因此在定数截尾的情形下[2-3],研究寿命分布参数的Bayes估计是十分必要的.目前还没有对三参数Weibull-Poisson分布的相关研究.
三参数Weibull-Poisson分布简称为WP(λ,m,β),其分布函数和密度函数分别为

本文研究当m,β已知时,参数λ的Bayes估计问题.
1 预备知识
定义1[4]Linex损失函数的定义为

定义2[5]复合Mlinex对称损失函数的定义为

引理 1[4]记为 λ在损失函数(1)下的Bayes估计,则
引理 2[5]记为 λ在损失函数(2)下的
2 主要结果
2.1 后验分布
在定数截尾情形下,设来自三参数Weibull-Poisson分布的一组容量为n的样本,观测值从小到大排列,前r个观测值依次为x1,x2,…,xr(为方便运算,此处省略了x(i)下标i的括号).则 x=(x1,x2,…,xr)的联合分布密度为

定理1 参数λ的先验分布选择广义均匀分布,即 π(λ)=1,λ∈(0,M),其中 0<M≤∞ ,则 λ的后验密度为
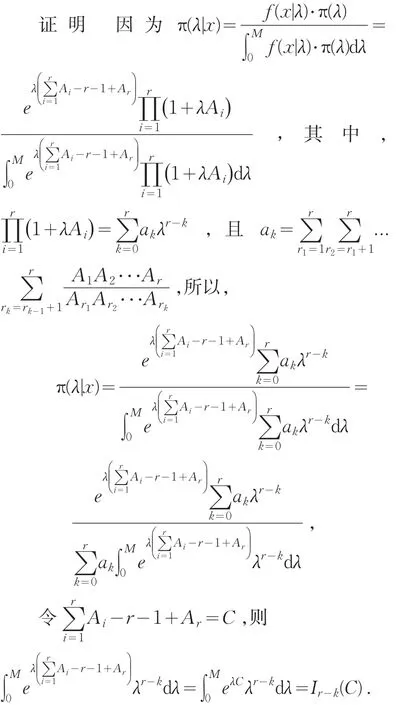

2.2 Linex损失下的Bayes估计
定理2 在损失函数(1)下,取三参数Weibull-Poisson分布先验分布为广义均匀分布,则参数λ的Bayes估计为证明 因为E根据引理
2.3 复合Mlinex对称损失下的Bayes估计
定理3 在损失函数(2)下,取三参数Weibull-Poisson分布先验分布为广义均匀分布,则参数λ的Bayes估计为
3 结论
本文主要研究了三参数Weibull-Poisson分布的Bayes估计问题.在定数截尾情形下,先验分布选取广义均匀分布时,在Linex损失函数和复合Mlinex对称损失函数下,给出了三参数Weibull-Poisson分布参数的Bayes估计.
猜你喜欢
数学物理学报(2022年1期)2022-03-16 06:15:24
工程与建设(2019年5期)2020-01-19 06:22:26
成都信息工程大学学报(2019年3期)2019-09-25 08:31:14
意林(2019年9期)2019-06-02 16:59:40
世界文化(2019年2期)2019-03-27 16:30:18
中学生数理化·高二版(2017年3期)2017-07-07 08:47:25
自动化学报(2017年5期)2017-05-14 06:20:44
探测与控制学报(2015年4期)2015-12-15 15:00:56
东南法学(2015年2期)2015-06-05 12:21:36
长春工业大学学报(2012年1期)2012-07-14 07:07:24

