数学建模促进大学数学教学改革

王志高　王永柱

【摘 要】数学建模活动作为高校科技实践教学活动的一个重要组成部分，对基础数学课程教学的改革有着越来越重要的作用。本文数学计算可视化、便利化;数学理论实用化的角度通过实际的案例展示了零点存在定理和均匀分布在数学建模中的精彩应用，让枯燥的基础数学知识点的讲授变得有趣、有用，对学生数学学习的实现正面情绪激励，体现了数学建模对基础数学教学改革的促进作用。

【关键词】数学建模;计算可视化;零点存在定理

中图分类号： G712;O1-4文献标识码： A 文章编号： 2095-2457（2019）35-0271-002

DOI：10.19694/j.cnki.issn2095-2457.2019.35.131

1 数学模型相关的软件计算对教学改革的影响

传统的大学数学教学，知识内容更新缓慢，知识点之间的次序结构相对稳定，教学方法沿袭了课堂讲授、课下安排大量作业题的方式。在课堂教学环节方面，随着多媒体教学的兴起，使得数学课堂教学朝着泛多媒体教学化的方向发展，但其本质还是把之前需要在黑板上一步一步写下来的演算或者讲解过程，提前写在ppt上面，而实质内容上变化不大。

数学建模竞赛的发展以及公共数学课课堂教学效果不佳的现实，促使大学数学老师在教学环节中更加重视一些数学建模案例和数学软件的应用。使其跟大学数学课堂教学紧密结合。

大学数学教学过程中关于极限、函数性质是一个重点，同时也是学生从中学的初等数学学习向大学的高等数学学习转变的一个关键难点。老师应用数学软件通过画图、计算把一些原本不容易看到、不容易得到的结果展示给学生，这样学生在学习过程中就会一下子豁然开朗，对概念的理解和方法的掌握就会更顺利。

比如在微积分[1]课程《无穷大量和无穷小量》的讲解过程中，有这样的一个结论“无穷大量是无界的，但是无界的变量不一定是无穷大量”。老师要给学生讲清楚这个事情，需要复杂的教学语言的组织。

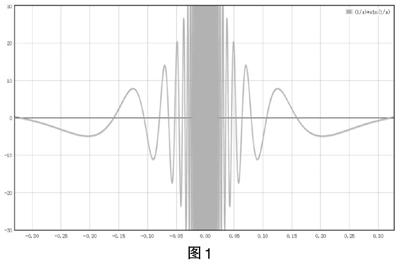
例1：函数y=■sin■在x→0时无界但不是无穷大量。

解：对于任意给定的M>0，

（1）xk=■，（k=0，1，2，3…），？圯y（x■）=2kπ+■

当k>M时，y（x0）>M，所以无界

（2）xk=■，（k=0，1，2，3…），？圯y（x■）=0

所以不是无穷大量。

上面数学证明是正确的，但是学生在听课的时候，并不能很快接受。

图1

此时如果用数学软件画出函数的图像，学生就可以非常形象的感受到在x→0时函数的变化过程（可以通过调节两个坐标轴的尺度，放大局部的图像，更好的感受图像的特点），就可以很好理解上述的数学证明。

再比如在线性代数课程的学习中，四阶以上的行列式的计算[2]是学生比较发愁的一个事情。老师在相关内容的讲授过程中，可以在传统课本知识的讲授基础上，再给学生添加相关的学软件的计算展示。

例2：计算行列式D=■，

传统方法需要用的行列式的五条计算性质以及按行按列展开，需要花费较长的时间，并且很容易出错。如果利用软件去计算的，非常的简单直接一行命令就可以。

以matlab软件为例：

先输入矩阵：D=[-2 2 -4 0;4 -1 3 5;3 1 -2 -3;2 0 5 1];

在执行计算：D=det（D）

可以在不到一秒钟之内看到结果：D=-270

在老师增加了软件计算的展示后，学生对数学计算题会有更多的思考，也掌握更灵活的处理方法。让数学建模相关的数学计算软件与传统的数学课堂教学内容交叉，可以让学生对所学的数学知识理解更深刻，掌握更灵活，课堂也更生动。

2 数学建模相关案例对基础数学教学改革的影响

传统的大学数学知识内容几十年没有什么变化，甚至大学数学在学生的心目中已经成为了枯燥、无用的形象。这样在学生们学习数学知识的时候就会天然的带着一种抵触的情绪，使得本来就尴尬的大学数学教学变得处境更加艰难。一些优秀的数学建模案例的出现，恰好可以去改变这一局面。

函数连续性是微积分中的一个重要内容，在函数连续性相关的性质中，零点存在定理是一个很简单的知识点，学生们往往觉得这么简单定理，一看就会，没什么意思，学了也没什么用处。现在给出数学建模中一个案例，从中可以看到零点存在定理的应用。

例3： 把椅子往不平的地面上一放，通常只有三只脚着地，放不稳，然而能否稍挪动几次，就可以四脚着地，放稳呢？

分析：解决问题之前，做些合理的假设，使得问题简化。

（1）椅子四条腿一样长，椅脚与地面接触可视为一个点，四脚的连线呈正方形。

（2）地面高度是连续变化的，沿任何方向都不会出现间断（没有像台阶那样的情况），即地面可视为数学上的连续曲面。

（3）对于椅脚的间距和椅脚的长度而言，地面是相对平坦的，使椅子在任何位置至少有三只脚同时着地[3]。

圖2

首先用变量表示椅子的位置，由于椅脚的连线呈正方形，以中心为对称点，正方形绕中心的旋转正好代表了椅子的位置的改变，于是可以用旋转角度θ这一变量来表示椅子的位置。

其次要把椅脚着地用数学符号表示出来，如果用某个变量表示椅脚与地面的竖直距离，当这个距离为0时，表示椅脚着地了。椅子要挪动位置说明这个距离是位置变量的函数。

由于正方形的中心对称性，只要设两个距离函数就行了，记A、C两脚与地面距离之和为f（θ），B、D两脚与地面距离之和为g（θ），显然f（θ）、g（θ）>0，由假设2知f（θ）、g（θ）都是连续函数，再由假设3知f（θ）、g（θ）至少有一个为0。当时θ=0，不妨设g（θ）=0，f（θ）>0，这样改变椅子的位置使四只脚同时着地，就归结为如下命题：

命题 已知f（θ）、g（θ）是θ的连续函数，对任意θ，f（θ）*g（θ）=0，且g（0）=0，f（0）>0则存在θ0，使f（θ0）=g（θ0）。

解：将椅子旋转90°，对角线AC和BD互换，

由且g（0）=0，f（0）>0可知g■>0，f■=0。

令F（θ）=f（θ）-g（θ），则F（0）>0，F■<0，

由f（θ）、g（θ）的连续性知F（θ）也是连续函数，

由零点定理，必存在θ0使F（θ）=0，即f（θ0）=g（θ0），

由f（θ）*g（θ）=0，所以f（θ0）=g（θ0）=0

通过这样一个数学模型的讲解，同学们对数学知识的掌握会更为深刻，对数学本身的情感认知会发生好的转变：数学还挺有意思，挺奇妙。尤其是在大学刚开始的时候给学生们讲这样一个案例，会极大的吸引学生，让学生对大学数学的学习充满兴趣。同时对改进大学数学课堂教学有非常大的帮助。

【参考文献】

[1]郑红芬.微积分[M].上海，上海交通大学出版社，2015.12.

[2]同济大学数学系，线性代数[M].上海，同济大学出版社，2015.

[3]姜启源，谢金星，叶俊.数学模型[M].高等教育出版社，2015.