基于精英策略和Levy飞行的粒子群算法
张 超,贺兴时,叶亚荣
(西安工程大学 理学院, 陕西 西安 710048)
0 引 言
粒子群优化算法[1](PSO)是由Kennedy和Eberhart提出的一种群智能随机优化算法.它具有结构简单、收敛速度快等特点.自提出以后,粒子群算法已经被广泛用于许多领域.比如数据挖掘[2],模式识别与分类[3],信号控制[4],Steiner树问题[5],旅行商问题[6].粒子群优化算法对于单峰函数的优化,具有良好的效果,但是对于多峰函数优化,却经常发生早熟过早收敛,从而不能很好求出全局最优值.针对粒子群算法易过早收敛的问题,很多学者提出了改进方法.如文献[7] 将粒子群算法应用于布谷鸟搜索算法中,提高布谷鸟搜索算法的收敛速度和计算精度.文献[8]提出了一种粒子群算法与人工鱼群算法的混合算法,该算法将人工鱼群的公告板、群聚和随行策略的模式应用于粒子群的速度与位置变更中,从而提高了粒子的搜索精度和搜索效率;文献[9]将粒子群算法与模拟退火算法相结合,新混合算法在粒子群算法搜索停滞时,在最优位置用模拟退火算法继续搜寻最优解.新混合算法具有收敛速度快,求解精度高的特点;文献[10]将粒子群算法与蚁群算法相结合,新混合算法中添加交叉与变异、和免疫选择等过程,实验结果表明该混合算法提高了算法的全局寻优能力.文献[11]利用反向学习策略和具有Levy飞行特征的改进搜索策略对出现停滞的粒子进行判断.实验结果验证了该算法在前期的搜索能力和后期的搜索精度上都优于其他几种算法.由此可见,将不同的智能算法结合或者引入其他搜索机制的思想可以很好的改善算法的性能.本文针对标准粒子群算法已陷入局部最优的缺陷,提出了一种基于精英策略和Levy飞行的粒子群算法,通过引入精英策略的思想和Levy飞行机制来提高粒子群算法的搜索效率,避免粒子陷入局部最优.使算法具有更快的收敛速度和更高的收敛精度.
1 粒子群算法与精英策略
1.1 标准的粒子群优化算法
粒子群算法是一种群智能优化算法, 粒子当前位置的优劣是由被优化的函数适应度值来评价.如果粒子种群是由N个粒子构成,在D维搜索空间中, 向量Xi=(xi1,xi2,…,xid),i=1,2,…,N.表示第i个粒子在搜索空间中的位置,向量Vi=(vi1,vi2,…,vid)表示粒子的速度,Pi=(pi1,pi2,…,pid) 表示第i个粒子搜索到的最优位置,Pg=(pg1,pg2,…,pgd)表示整个粒子群能搜索到的最优位置.则粒子的更新方程为
vid(t+1)=ωvid(t)+c1r1(pid-xid(t))+c2r2(pgd-xid(t)).
(1)
xid(t+1)=xid(t)+vid(t+1).
(2)
式中:d=1,2,…,D;ω称为惯性权重;c1和c2称为学习因子;r1和r2为2个随机数;它们在(0,1)内取值;当前迭代次数为t.
1.2 精英反向学习策略
1.2.1 精英反向学习 反向学习(opposition-based learning)的概念是由Tizhoosh[12]于2005年提出的,它可以较好地缓解粒子过早收敛的问题.在考虑当前粒子的同时考虑其反向粒子,增大了粒子的搜索空间,改善算法的性能,使粒子避免过早收敛,实现全局寻优.

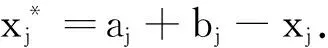
(3)
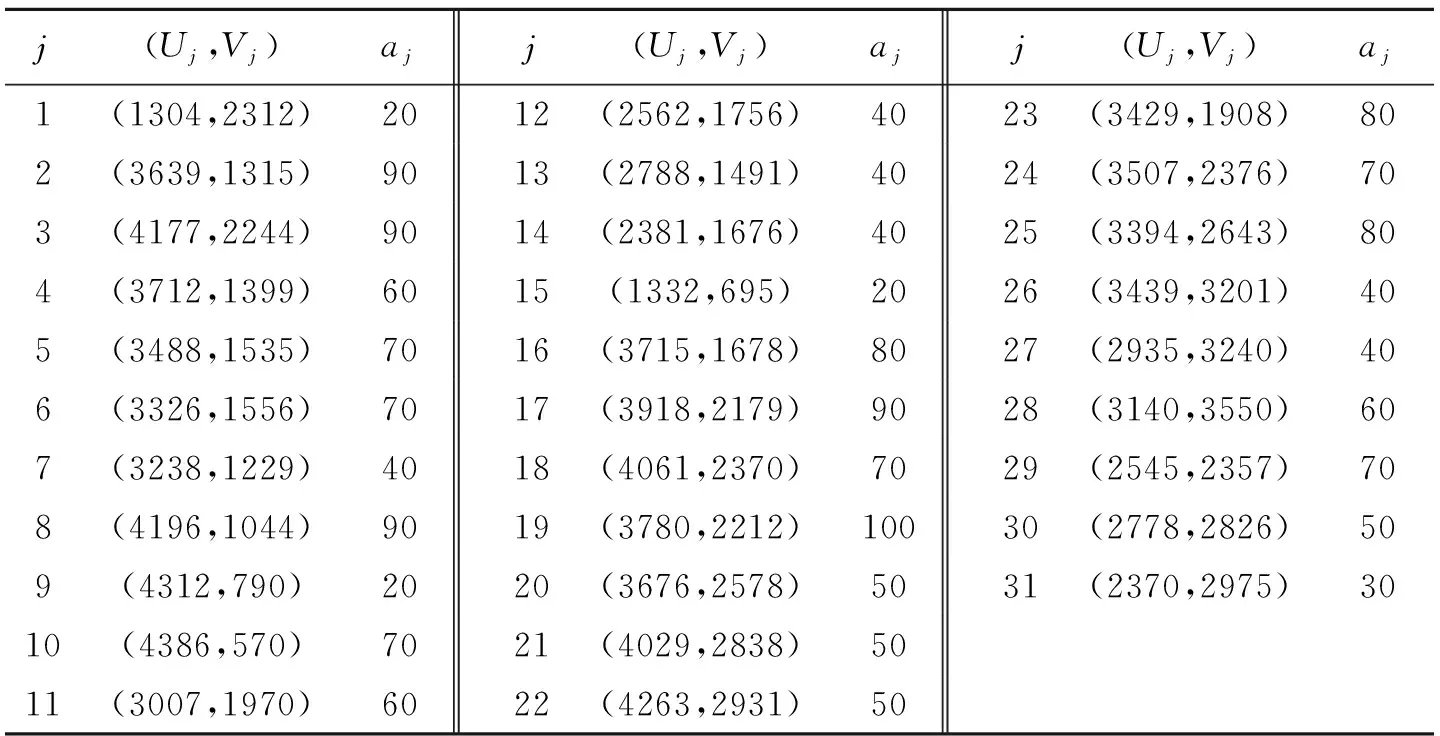
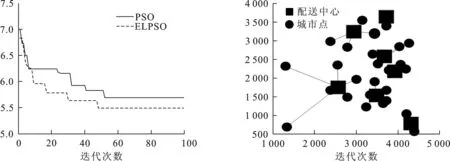
定义2[13]基于反向解的优化(opposite-based optimization).如果待求解的优化问题是求最小值,f(*)评估函数,通过f(*)计算候选解的适应度值,如果待求解的优化问题的可行解是X,X*是X的反向解;如果f(X*) 定义3[13]动态反向学习(dynamic generalized opposition-based learning). (4) (5) 1.2.2 Levy飞行 Levy分布是由法国数学家莱维 (Levy) 提出的一种概率分布,之后很多研究者对Levy分布进行了大量的研究.截至目前, 自然界的很多动物觅食轨迹遵从Levy分布(Levy distribution)[15]的事实已经得到了证明.Levy飞行服从Levy分布[16].很多随机现象的原理,如布朗运动、随机行走等遵从Levy飞行.目前Levy飞行在智能优化领域已经被广泛应用,比如布谷鸟算法中就采用Levy飞行进行位置更新[17],Levy飞行可以扩大搜索空间, 因此把Levy飞行引入智能优化算法中更容易使算法避免过早收敛[18].Levy飞行位置更新式为 (6) Levy~u=t-λ,1<λ≤3. (7) Levy飞行实质是一种随机步长,其步长遵从Levy分布,由于Levy分布比较复杂,所以Levy分布通常由Mantegna算法来模拟实现,步长s计算为[19] (8) 式中:μ,v为正态分布,定义 (9) (10) 式中: (11) σν=1. (12) 式中:β通常取值为常数1.5. 1.2.3 自适应动态步长 由于Levy飞行中的步长α为固定常数,导致在搜索过程中存在搜寻能力差,搜索精度低的问题,本文提出自适应动态函数步长α1来代替α.由于寻优初期粒子位置更新变化较大,需要较大步长,使粒子个体能快速寻找到最优解;寻优后期,需要较小步长来提高最优解的精度,因此需使步长的变化呈递减趋势.步长的改进为 (13) 将式(13)代入式(6)可得到改进之后的自适应Levy飞行步长公式,即 (14) 利用精英粒子的良好反向搜索能力,以及自适应动态Levy飞行更新因早熟而无法进化到更好位置的粒子,进行算法的进一步优化.具体步骤为 (1) 种群初始化. (2) 依据精英策略产生精英反向个体,将每个粒子的适应度值计算出来,并且将粒子的适应度值存储在pbest中,从当前个体和精英反向个体中选择出适应度值最优的个体,让适应度值最优的个体作为下一代种群,并将最优个体的适应度值存储于gbest中. (3) 更新粒子的速度和位置.根据式(1)和(2)进行更新. (4) 更新个体最优.比较粒子更新前后的适应度值,取较好的粒子作为下一代粒子. (5) 更新全局最优.把pbest和gbest的值进行比较,如果pbest的值比gbest的值更优,那么把pbest的值赋值给gbest并使gbest进行更新. (6) Levy飞行.如果粒子位置停留在局部的迭代次数大于等于10.那么使用式(14)使粒子的位置进行更新.根据步骤(4)和(5)更新个体最优pbest和全局最优gbest. (7) 算法终止.如果算法符合迭代结束条件,则使算法停止运行; 否则返回步骤(3) 继续搜索. 为了检验ELPSO算法的性能,将ELPSO算法与标准PSO算法和RWPSO算法用于6个典型的测试函数中,并对结果进行比较. ELPSO算法的参数设置如下: 粒子数为N=50,维数为D=10,迭代次数为150次,c1=1.496 2,c2=1.496 2,w=0.729 8,p=0.25,p为执行精英反向学习的概率.Levy飞行的参数β设置为1.5.RWPSO算法为权重线性递减的改进粒子群算法,它的参数除过w,p,β这3个参数与ELPSO算法有所不同之外,其他参数均与ELPSO算法参数相同,本次实验选取了6个典型的测试函数,表1给出了本次实验测试函数的特征. (5) Booth函数f5(x)=(x1+2x2-7)2+(2x1+x2-5)2. 表 1 函数的基本特征Table 1 Basic features of the function 3.2.1 实验一 对PSO算法、RWPSO算法和ELPSO算法的平均适应值,方差Best值,Worst值进行比较.在不同维数下,3种算法独立实验50次所得到的结果见表2. 由表2可知,ELPSO算法的平均适应值和方差的算法精度显著高于PSO算法和改进的RWPSO算法,说明ELPSO算法性能比PSO算法和RWPSO算法的性能更好. 表 2 6个测试函数的均值、方差、Best及Worst比较Table 2 Comparison of mean, variance, Best and Worst of 6 test functions 3.2.2 实验二 图1是3种算法针对不同测试函数的进化曲线图. (a) Ackley函数 (b)Beale函数 (c) Griewank函数 (d) Levy函数 (e) Booth函数 (f) Rosenbrock函数图 1 6种测试函数的收敛曲线Fig.1 The convergence curve of six test functions 对于Ackley函数,进化初期ELPSO算法的收敛速度明显快于RWPSO算法和PSO算法,随着迭代次数的增加ELPSO算法快速收敛,在较少的迭代次数下寻找到全局最优值.对于Beale函数,在进化后期阶段RWPSO算法和PSO算法收敛较慢,而ELPSO算法能保持很快的速度收敛.对于Griewank函数和Levy函数,在进化前期PSO算法和RWPSO算法能较快的收敛,随着迭代次数增加,PSO算法和RWPSO算法收敛速度变慢甚至出现停滞,而ELPSO算法始终能保持很快的速度收敛.对于Booth函数,在进化的整个过程中ELPSO算法的收敛速度都快于PSO算法和RWPSO算法.对于Rosenbrock函数,在PSO算法出现停滞以及RWPSO算法收敛速度变缓的情况下,ELPSO算法仍保持着很快的速度收敛. 分析图1可知,ELPSO算法的性能比RWPSO算法和PSO算法的性能更好,在迭代次数相同的情况下,ELPSO算法的收敛速度更快且精度更高.ELPSO算法在寻优过程中,依据精英反向学习,选择适应度值较好的个体作为下一代个体,使算法的全局搜索能力得到了提高.利用Levy飞行机制来更新个体的位置,提高了粒子的跳跃能力,可以使其避免过早收敛.ELPSO算法显著提高了PSO算法的精度和收敛速度,具有更优的性能. 表 3 ELSPO算法与PSO算法和 RWPSO算法的T检验Table 3 T-test of ELSPO algorithm and PSO algorithm and RWPSO algorithm 3.2.3 实验三 统计检验.在实验中,3种算法在6种测试函数上均独立运行40次,因此对于单独的测试函数,每种算法都得到40个样本.采用T检验法对PSO算法,RWPSO算 法,ELPSO算法的性能进行比较.该T检验采用显著水平为0.05的双尾检验.实验结果为 “=”或 者 “+”.“=”表示在相同的测试函数上ELPSO算法与PSO算法或者RWPSO算法显著性相同,“+”表示ELPSO算法的显著性比PSO算法或者RWPSO算法更优.从表3中可以看出,ELPSO算法的显著性比PSO算法和RWPSO算法更优. 3.2.4 实验四 为验证算法的有效性,收集了全国31个城市的坐标,每个用户的位置及物资需求量由表4给出,这里的物资需求量是经过规范化处理之后的数据,不代表实际值.从中选择6个作为物流配送中心.依据本文算法步骤对上述问题进行求解,算法的参数分别为:种群规模为50,迭代次数为100次. 表 4 用户的位置及其物资需求量Table 4 User′s location and its material requirements 表4中,j表示城市的序号,(Uj,Vj)表示用户的位置,aj表示物资需求量.改进的算法及原算法的收敛曲线如图2所示,得到的物流配送中心选址方案如图3所示. 图3中方框表示配送中心,圆点表示城市点,方框与点之间有连线表示该城市的物资由连接的配送中心配送.实验结果表明改进的算法比原算法收敛更快,更有效. 图 2 2种算法的收敛曲线 图 3 物流配送中心选址方案Fig.2 Convergence curves of the two center Fig.3 Location plan of logistics distribution algorithms 本文针对PSO算法容易陷入局部最优的缺陷,将精英策略和自适应动态Levy飞行步长引入到 PSO算法中,扩大粒子的搜索空间,使粒子避免过早收敛.选取6种测试函数对ELPSO算法进行仿真实验,仿真结果表明ELPSO算法在相同迭代次数下比PSO和RWPSO算法收敛速度更快、精度更高;t检验结果更说明ELPSO算法比PSO和RWPSO算法更具优越性.最后通过物流中心选址的算例对改进的算法进行测试,实验结果表明本文能更快收敛到全局最优解,求解的精度也更好,能很好地解决物流中心选址问题.本文提出的改进算法不是唯一的,还可以尝试与其他算法结合,寻找更加高效的实现全局寻优的智能优化算法.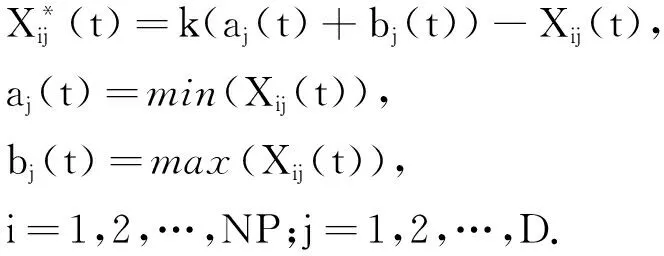
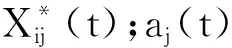
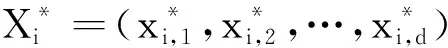

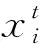


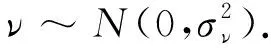
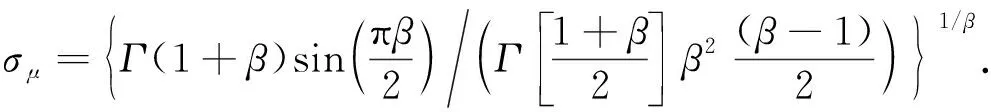
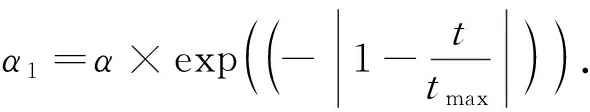
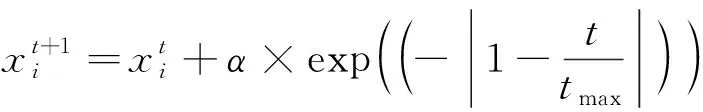
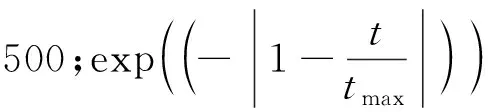
2 改进算法—ELPSO
3 仿真实验
3.1 实验设计

3.2 结果分析




4 结束语

