6种交叉操作两两搜索区域大小的定量分析

赵新超，陈 敏，巩敦卫

(1.北京邮电大学理学院，北京 100876;2.中国矿业大学信息与控制工程学院，江苏 徐州 221116)

0 引言

遗传算法是由Holland[1]于1975年提出，它是一类借鉴生物界自然选择和适者生存机制的随机搜索算法[2-4]。遗传算法在迭代过程中保留一组候选解，利用交叉、变异等遗传操作产生新的候选解群体，按照适应值指标从解群体中选择较优个体进入下一代，重复此过程，直到满足某种收敛指标。遗传算子仅仅利用适应值作为度量指标进行随机操作，降低了一般优化算法在搜索过程中对问题信息和人机交互的依赖[5]。与传统的优化算法[6]相比，遗传算法的主要特征在于不依赖于问题的梯度信息与群体搜索策略，群体搜索使得遗传算法得以突破邻域搜索[7]的限制，可以实现整个解空间上的分布式信息采集和探索。

在遗传算法中，交叉算子通过模拟自然界生物的杂交过程对个体进行交叉操作，不断产生新个体，增加种群的多样性，扩大寻优范围，从而使得遗传算法具有较强的全局搜索能力。因此，交叉算子在遗传算法扩展求解空间和搜索全局最优解的过程中发挥着重要作用[8]。对实数编码的交叉策略[9]，两个父体经交叉操作后得到的子个体往往限定于两父体围成的某个区域，使整个群体搜索范围和路径探测受到了一定的限制，并有早熟收敛于局部邻域的可能。子个体若要跳出父体围成的区域，一般只能借助于变异操作，但若单纯地加大变异概率或增大搜索步长，遗传算法就有退化成一般随机搜索算法的趋势[10-11]。针对这一不足，文献[12]提出了几种新的交叉算子，对传统的交叉操作进行了相应的改进，使得子代个体始终有跳出父体所围成区域的可能，一定程度上扩大了遗传算法交叉算子的搜索区域，使算法始终保持探测新区域的可能。但是，该文献只是给出每组交叉操作搜索区域大小比较的定性结果，并没有任何定量的理论分析和数据支撑。本文对文献[12]中6种实数编码的交叉操作的相对搜索区域和潜在的覆盖范围进行了定量分析和理论探讨，为交叉算子和遗传算法的算法设计[13]以及问题求解提供了理论支持。

1 6种实数编码的交叉操作

序列投影寻踪是揭示隐藏在高维数据中有趣结构的有用工具[12]，并有序地构造了低维空间的基底。遗传算法是发现这些基底的有力工具，但是它的表现取决于对遗传算法交叉操作的选择。Espezua等[12]对8种交叉操作进行了介绍和比较分析，多组测试结果表明，新提出的超圆锥交叉操作在寻找适应度最高的投影方面表现最好。

下面对其中的6种(3组)实数编码的交叉操作进行介绍，详细的操作参见文献[12]。下面都假定a1与a2是两父代个体，b1与b2是两个子代个体。

1.1 算术内部交叉(交叉1)

算术交叉操作产生子代的过程如下：

b1=Normalize(ra1+(1-r)a2)，b2=Normalize((1-r)a1+ra2),

(1)

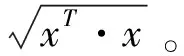
1.2 算术内外交叉(交叉2)

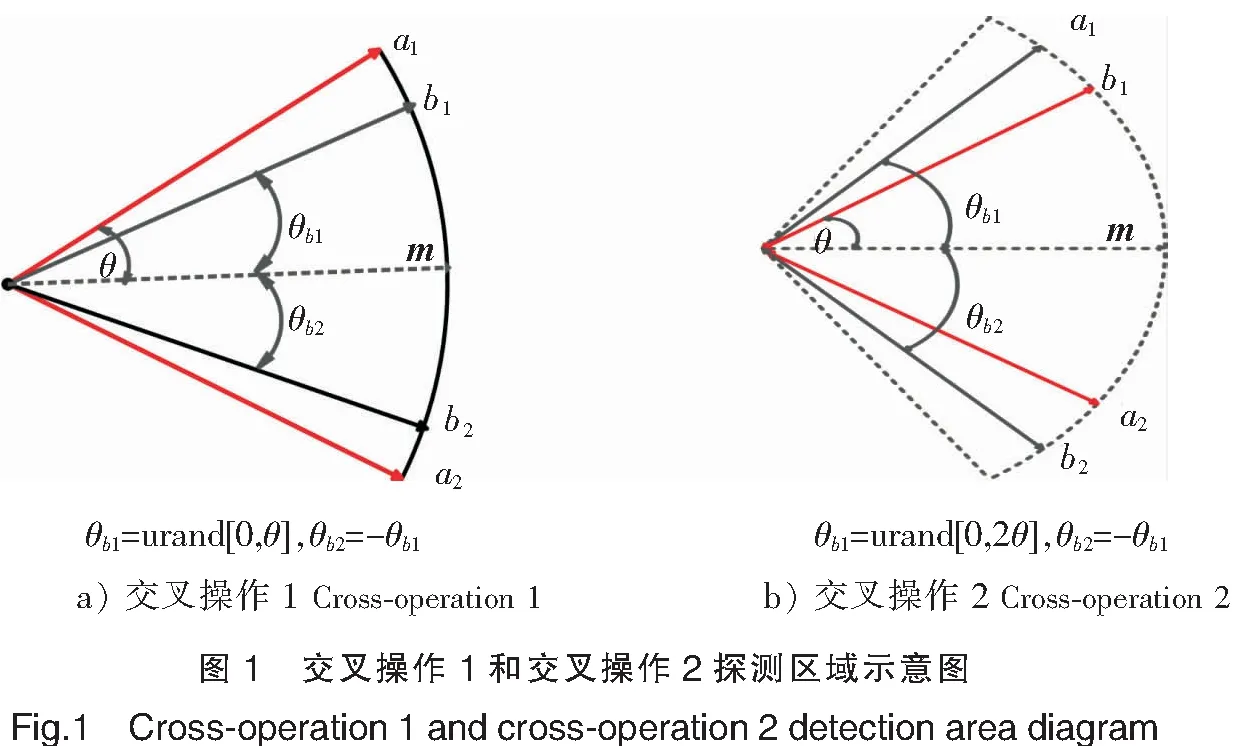
该算子是对交叉操作1的拓展，子代产生方式同交叉操作1，唯一的区别是随机数r的产生范围由[0,0.5]变成[-0.5,0.5]。因此，子代向量有较大可能位于父代向量围成的扇形区域之外，并依然对称地分布在父代等分线的两侧，操作如图1b所示。相比于交叉操作1，交叉操作2的子代可以产生在由父代个体向量形成的扇形区域之外，在这个扩展的扇形区域中，子代和对称轴形成的最大角为2θ，θ是父代个体和对称轴之间的夹角，该操作的探测范围和新解的生成过程如图1b所示。

1.3 内部超圆锥交叉(交叉5)

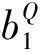
1.4 内外超圆锥交叉(交叉6)

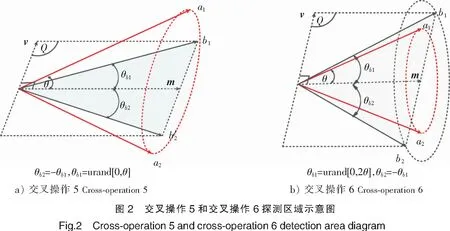
该交叉操作是交叉操作5的扩展，产生子代的步骤类似于交叉5，唯一的区别是此时θr∈[0,2θ]。对比于交叉操作5，通过父代个体围绕等分线进行旋转产生的子代可以在超圆锥体的外部，因此，子代个体产生了相对更广泛的超圆锥搜索邻域。

交叉操作5和交叉操作6的邻域探测范围和子代产生的过程如图2a和图2b所示，θ是父代向量a1或a2与其夹角平分线m的夹角，θb1，θb2是子代个体b1和b2与对称轴的夹角，urand[a,b]是均匀分布在区间[a,b]的一个随机数。

1.5 适应度偏向的内部交叉(交叉7)

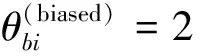
(2)

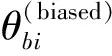
1.6 适应度偏向的内外交叉(交叉8)

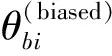
2 3对交叉操作搜索区域对比的定量分析

2.1 交叉操作1和交叉操作2

由于交叉操作1和交叉操作2中子代产生的范围由父代个体形成的扇形区域所界定，又因为扇形面积公式为S=αr2/2，其中r为扇形半径，α为扇形圆心角，并且由相同的两个个体在交叉操作1和交叉操作2中所围成扇形的半径相同，而交叉操作2产生的子代个体探测扇形区域的圆心角是交叉操作1产生子代的2倍，所以子代个体搜索区域的面积也是交叉操作1中的两倍，即交叉操作2产生子代的搜索探测范围较交叉操作1更广泛，子代样本能保持较好的探测空间多样性，尤其是算法搜索的后期，更有利于保持群体多样性，从而更有可能跳出当前邻域，更好地寻求全局最优解。

2.2 交叉操作5和交叉操作6

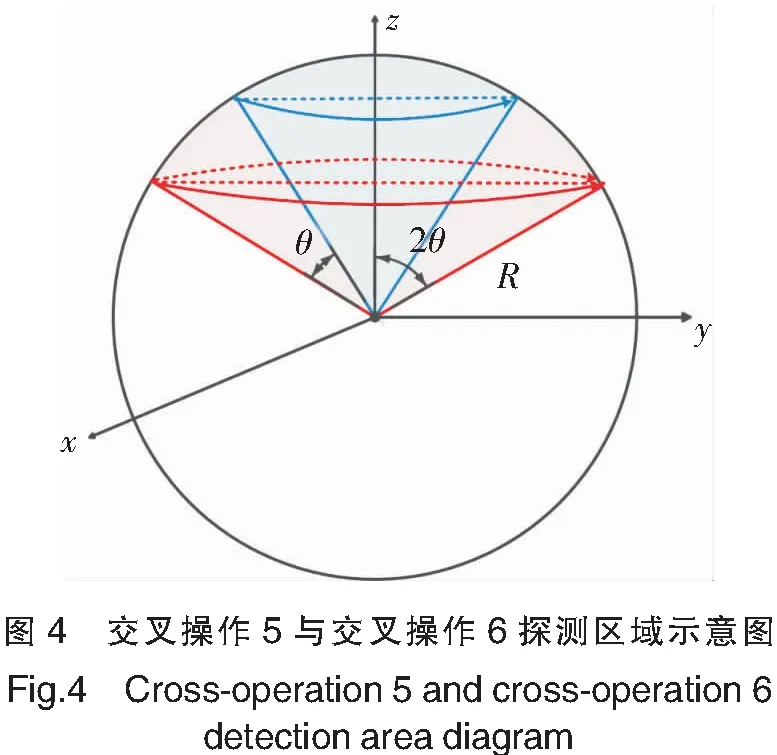
由于交叉操作5和交叉操作6产生的子代覆盖区域是其两父代个体绕其中心线旋转形成的圆锥和圆锥所对应的球冠内部，即为圆锥体顶角所对应的包含于球体内部的那一部分球体体积，所以两种交叉操作对应的搜索区域之比就是它们子代个体所可能张成的圆锥和球冠的体积之比。如图4所示，其中蓝色阴影部分代表交叉操作5产生子代个体所可能覆盖的区域体积V5，蓝色和红色阴影部分之和代表交叉操作6产生子代个体所可能覆盖的区域V6。

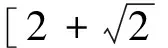
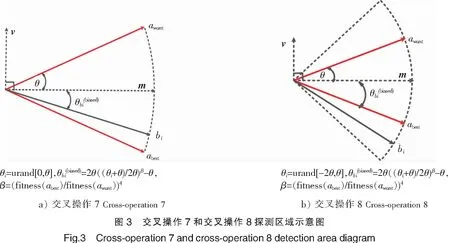
2.3 交叉操作7和交叉操作8

由于交叉操作7、交叉操作8与交叉操作1、交叉操作2类似，区别在于交叉操作1和交叉操作2是在可能的探测范围内均匀地产生子代，而交叉操作7和交叉操作8是以依赖于个体适应值的非均匀方式产生子代个体，因此若只是考虑探测范围的区别，这两组操作有相同的探测范围的对比分析，因而仅仅考虑探测范围显示不出交叉操作7、交叉操作8与交叉操作1交叉操作2的区别。根据交叉操作7和交叉操作8的特点分析可知，这组交叉操作的更重要特征是子代个体在允许的探测范围上的非均匀分布。由于较优父代个体与中心线夹角为负，因此该组交叉操作对比的重点在于考察操作8产生的子代个体是否有更趋向于较优父代个体邻域的趋势，如果有该趋势，可否分析出这种趋于较优个体趋势的大小。

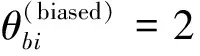
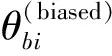
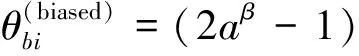
通过以上对遗传算法中的6种交叉操作的两两定量对比分析，给出了两两搜索区域和覆盖范围大小比较的解析结果，证明了新的交叉操作比相应的原有操作具有相对的广邻域性，从而对新的交叉操作具有相对的优异性能给出可靠的理论分析基础。不仅加深了对遗传算法的执行机理的理解，还在一定程度上给遗传算法概率型搜索的黑箱搜索机制提供了理论支持。

3 结论

对文献[12]中6种(3组)实数编码的交叉算子的探测区域进行了定量对比分析。通过对每一对交叉算子所可能的搜索区域和覆盖范围进行理论上的对比分析发现，每一对交叉算子中的后者对应的搜索区域都比前者更加广泛，即后者的交叉操作有效扩大了种群多样性和寻优范围，体现了扩展的交叉操作具有内在的群体多样性保持机制和搜索的宽邻域特性，从而使得遗传算法具有更加平衡的搜索能力，有效减少了交叉操作在求解过程中陷入局部最优解的概率，而这种性能对群体优化算法具有重要影响，尤其是算法搜索后期。综合本文对不同组交叉操作探测范围的理论对比分析和文献[12]中对不同交叉操作的实验对比分析，证明了本文中对6种(3组)交叉操两两作对比分析的正确性和必要性，从而为遗传算法搜索性能的差异表现提供了理论上的支持。