高速列车单节车体空气动力特性优化

方 正，王大镇

(集美大学机械与能源工程学院，福建 厦门 361021)

0 引言

随着列车运行速度的提高，气动效应对高速列车的影响加剧，空气阻力、列车风和侧风稳定性等空气动力学问题日益显著，其中侧风作为列车动态限界的随机因素之一，其影响更加明显，比如在特殊环境下(如高架桥、山区风口和会车段)，车体会面临巨大的气动冲击载荷，列车车体上所承受的气动力和力矩会迅速增大，甚至可能会大到足以倾覆列车，因此为了保障列车运行的横向稳定性，有必要对侧风下列车的气动特性进行研究[1-4]。

文献[5]基于代理模型对车厢夹层板结构建立了以质量和最大变形为指标的优化模型，并采用多目标遗传算法NSGA-II对建立的模型进行了多目标优化。文献[6]采用Kriging代理模型对列车的悬挂参数进行了模型替代，并对其进行了区间优化。文献[7]基于径向基(RBF)神经网络对高速列车车头的气动特性进行了优化。相比较于Kriging代理模型和RBF神经网络，广义回归神经网络(GRNN)各层之间的权值由训练样本唯一确定，隐含层节点数也由训练样本自适应确定，由于调整参数少，使得GRNN网络更适合于小样本数据，并且其在收敛速度和全局收敛性上较RBF网络有着较强的优势。

本文选取列车车体的一个微单元，即单节车体为研究对象，以便为整体列车的模拟提供研究基础。为了确保列车单节车体模型的可靠性和准确性，同时考虑到广义回归神经网络(GRNN)的优点，本文运用广义回归神经网络对用流体动力学软件(Fluent)获得的单节车体的实验数据进行训练，以获得优化所需要的模型，采用遗传算法对该模型进行优化，并对优化前后的列车单节车体空气动力特性进行了对比分析。

1 计算原理和方法

1.1 计算模型

以某型高速列车的单节车体作为研究对象，本体截面示意图如图1所示，其中：L为单节车体长度；H为单节车体高度；R1和R2为过渡圆角半径；h和b为截面加筋的高度和厚度。列车单节车体在侧风流场中的运动可以被视为一个三维不可压缩粘性湍流流动，选择标准的k-ε方程作为湍流模型，其湍流方程[8-9]为：

∂(ρφ)/∂t+div(ρuφ)=div(Γgradφ)+S。

(1)

式中：ρ为空气密度，kg/m3；u为空气分子粘度，Pa·s；φ为任意通量，φ取1为质量守恒，φ若为速度则为动量守恒方程；S为源项；Γ为扩散系数。

相应的计算区域和边界条件如图2所示。其中：入口速度为20 m/s；出口为压力出口，静压为0；地面和单节车体表面定义为光滑无滑移的壁面边界条件。

定义气动力和力矩系数为[10-11]：

CS=FS/(0.5ρV2A)；CL=FL/(0.5ρV2A) ；CM=M/(0.5ρV2A3/2)。

其中：CS，CL和CM分别为侧向力、升力和倾覆力矩系数；FS，FL和M分别为侧向力、升力和倾覆力矩；ρ是空气密度；V是横风速度；A是单节车体侧面面积。

1.2 GRNN模型

广义回归神经网络(GRNN)是改进型径向基函数网络的一种变型，由于其非线性映射能力强，并且网络最后收敛于样本量聚集较多的优化回归面，因此在函数逼近，分类能力和学习速度方面具有较强优势[12]。GRNN网络中受到人为调节的参数较少，只有光滑因子，网络各层之间的连接权重由训练样本唯一确定，避免了在迭代过程中的权值修改，网络学习过于依赖于样本数据和人为主观假定对预测结果的影响[13]，因此本文采用GRNN网络对实验数据进行数据建模，其网络结构形式如图3所示。

同时为了更好地研究神经网络的拟合能力，定义相关系数R为

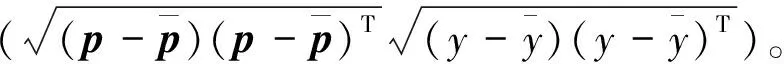
式中：p为随机向量；y为随机变量。

图4为测试数据和GRNN的输出对比结果，可以看出相关系数均接近于1，说明所建立的神经网络模型能较好地拟合数据。

1.3 计算方法

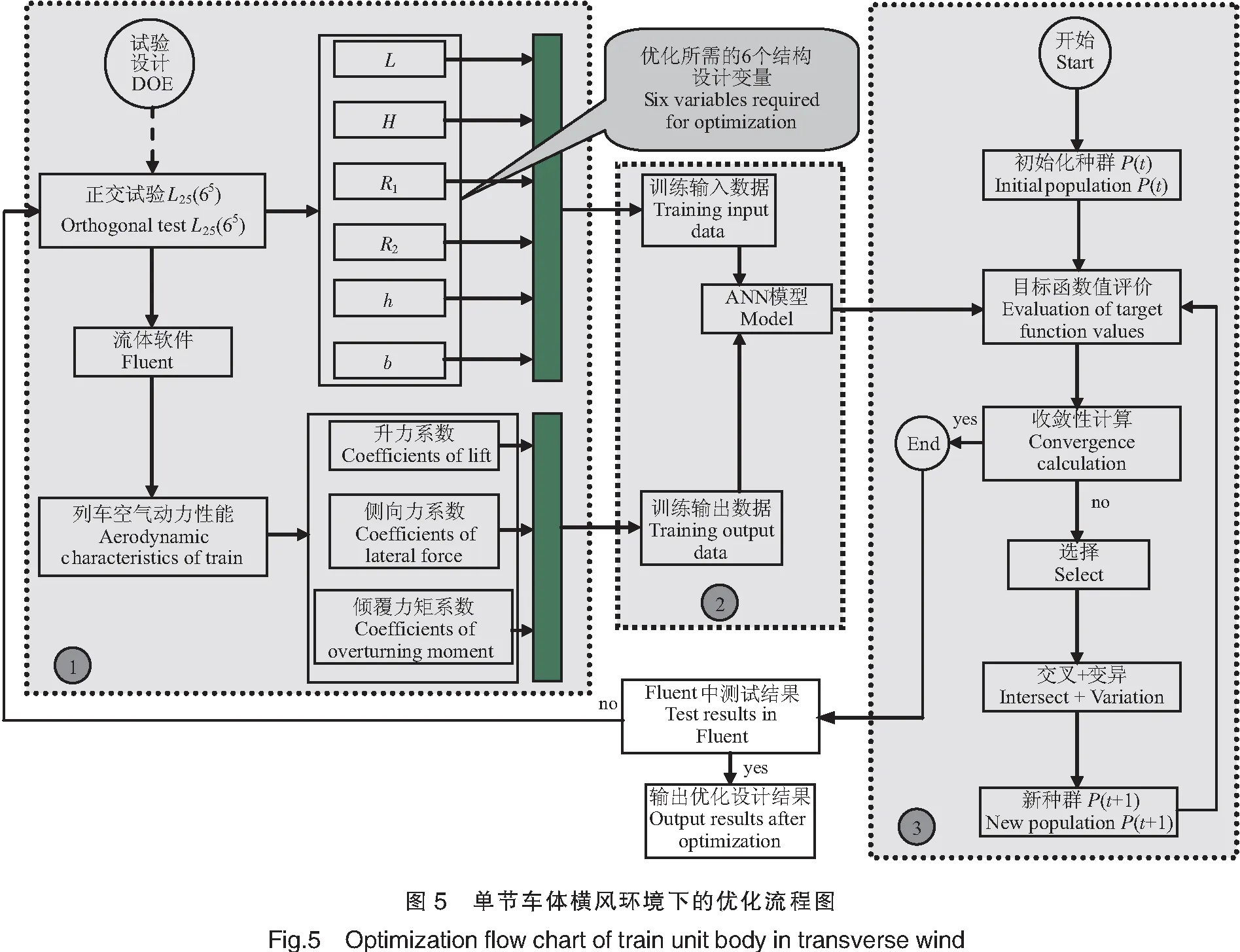
单节车体在横风环境下的计算方法流程图如图5所示。其计算主要步骤如下：

1)首先进行试验设计(DOE)，并在计算流体动力学软件(Fluent)中计算出单节车体的空气动力特性值；

2)将获得的仿真数据输入到GRNN网络中进行训练，以完成优化所需要的优化模型；

3)采用遗传算法对单节车体的结构参数进行训练，其适应度值函数选择最小化单节车体的最大倾覆力矩系数；

4)对得到的适应度值判断是否满足算法的终止条件，若满足，则退出算法，如果不满足，则重复遗传算法操作；

5)将获得的优化单节车体结构参数带入Fluent中进行验证分析，若满足要求，则输出优化设计结果。

2 计算结果分析

选取列车单节车体的初始参数值为{L，H，R1，R2，h，b}={3 000，3 800，600，400，50，2}，设置结构参数的优化范围为：3 000≤L≤3 400；3 800≤H≤4 200；675≤R1≤900；400≤R2≤800；50≤h≤70；2≤b≤6。同时设置遗传算法的群体数为100，变异概率为0.01，交叉概率为0.6。

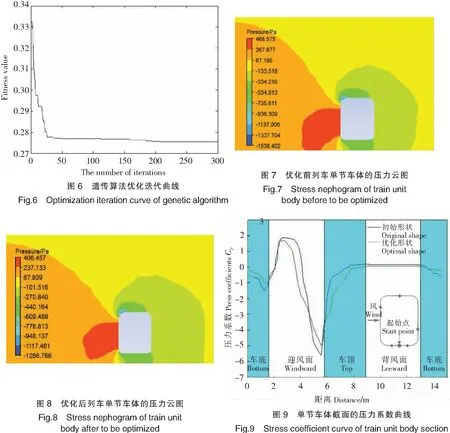
遗传算法的优化迭代曲线如图6所示，由图6可以看出，在迭代300次后，适应度函数值逼近一个常值，表明遗传算法收敛到最优解，其最优解为{L，H，R1，R2，h，b}={3 357.1，3 889.8，673.9，498.2，56.1，3.1}。优化后，其升力、侧向力和倾覆力矩系数分别降低了11.5%、8.05%和17.5%。

图7和图8为优化前后的压力云图对比，可以看出，优化后的单节车体的顶部和底面压力有所减少，同时迎风面的压力也有所缓解。

为了更好地说明优化后的单节车体的空气动力特性，选取列车单节车体中截面的压力系数进行分析，其结果如图9所示。

由图9可以看出，单节车体优化前后的压力系数有较大的不同，在单节车体的背风面，优化前后的差异不大，但是在车底和迎风面，优化后的压力系数有了较大的改善。这是因为与原有车型尺寸参数相比，车身顶部和底部圆弧半径的增加，减慢了通过气流加速进程。同时，优化形态的迎风面也由于列车单节车身高度的增加而增加，因此，列车气动性能得到改善。

3 结语

本文以某型高速列车单节车体为研究对象，针对传统高速列车单节车体空气动力特性优化方法的不足，采用广义回归神经网络对用流体动力学软件(Fluent)获得的单节车体的实验数据进行训练，以获得优化所需要的模型，采用遗传算法对该模型进行优化，对比优化前后的单节车体模型，发现优化后的升力、侧向力和倾覆力矩系数分别降低了11.5%、8.05%和17.5%，并且优化后的单节车体压力系数与原有单节车体相比得到了改善，提高了列车的空气动力特性。