一种基于Sentinel-1连续干涉像对的PSInSAR算法

刘 飞，潘 斌

(武汉大学遥感信息工程学院，湖北 武汉 430079)

地面沉降是一种缓慢变化的地质灾害，可引起城市建筑物倾斜，破坏地基的稳定性，给生产和生活带来很大影响。天津市在过去几十年中由于地下水开采过度遭受了严重的地表沉降灾害，研究如何有效地监测该地表沉降具有重要的理论价值和实际意义。

永久散射体差分干涉技术(PSInSAR)是近十几年来新兴的遥感技术手段。该技术具有对地表进行长时间、大面积、高精度形变监测的能力，是近些年来沉降监测的有效手段[1-4]。PSInSAR技术应用于多颗星载SAR卫星(如ERS1/2、Envisat、TerraSAR-X等)的数据处理上，在对地表形变监测的应用中可取得与地表数据相符合的测量精度。自2014年和2016年Sentinel-1A和Sentinel-1B发射成功后，其数据由于共享性，且具有更先进的成像方式、更短的重访周期及更精密的轨道控制等优点[5]，而成为新的研究热点[6-10]。

针对以往PSInSAR算法受限于数据条件，采用单主影像干涉组合方法而导致的低相干性、解算流程复杂等问题，本文研究针对Sentinel-1的数据特点，提出连续干涉像对的组合方法，利用相邻成像时间的2幅SAR影像生成干涉图，使时间基线导致的去相干最小化，提高相干性。在形变解算流程中，利用重访周期固定的特点，通过干涉图差分消去线性形变，在不影响形变解算的情况下，单独解算地形误差相位。本文以天津市为研究区，基于2016年11月至2018年1月32幅Sentinel-1B数据，采用新算法生成该地区的沉降速率图，并通过与水准数据比较验证新算法的有效性。

1 连续干涉像对与PS点选取

1.1 连续干涉像对

区别于传统PSInSAR单主影像干涉组合方法，连续干涉像对按照成像时间顺序，选择成像时间相邻的2幅影像两两生成干涉像对，即对于按成像时间获取的每幅影像而言，其既是下一幅影像的主影像，又是上一幅影像的辅影像。对于由N+1幅SAR影像生成的N幅连续干涉像对而言，其第i张干涉相位ψi有

ψi=φi-φi+1

(1)

式中，i=1,2,…,N；φi、φi+1分别表示第i张和第i+1张影像的相位值。

1.2 配准主影像选择

尽管对于任意一幅SAR影像而言，其选择时间上对应的上一幅影像作为主影像，但仍然需要从所有影像中选择一幅配准主影像，将其他所有影像与之配准，以满足后续的干涉图生成。配准主影像的选择需要使得总的配准去相干噪声最小化，其选择方式与传统PSInSAR选择主影像相同，配准去相干噪声ρtotal表达式为[11]

ρtotal=ρtemporal·ρspatial·ρdoppler·ρthermal

(2)

式中，ρtemporal、ρspatial、ρdoppler和ρthermal分别表示由时间基线、空间基线、多普勒中心频移及热噪声导致的去相干。

尽管理论上在选择配准主影像时要考虑上述所有因素，但对于Sentinel-1数据而言，由于具有更精密的轨道控制，无论选择哪幅影像作为配准主影像，空间基线都保持在一个较小的范围内，同时其数据的多普勒中心频移均很小，而热噪声在这个过程中被认为是常量，因此，时间基线便成了关键因素。为了尽可能减少由时间基线导致的去相干，通常选择靠近成像时间中心的影像作为配准主影像。

1.3 PS点选取

在配准生成连续干涉像对后，需要从干涉像对中提取相位稳定且相干性较高的点，即PS点，用于后续的相位解缠和形变解算。本文采用基于幅度离差[12]的方法先进行PS点的初步筛选，再根据PS点的相位特征[13]进行精选。

连续干涉像对和单主影像干涉像对在PS点的选取算法上大致相同。但由于连续干涉像对的相干性提高，生成的干涉图质量更优，使得稳定PS点的噪声降低，相位残差更小，PS点的选取更精准。同时单主影像干涉像对方法会引入由于主影像存在于所有干涉图上而产生的主影像误差，解算中需要额外求解此误差项，而连续干涉像对方法则避免了这一误差项，提高其解算精度。

2 形变相位解算

2.1 相位组成分析

在对选取的PS点进行三维相位解缠[14]后，对于给定像素点x，其在第i张干涉图上的解缠相位ψx,i为

ψx,i=ψD,x,i+ψA,x,i+ψS,x,i+ψθ,x,i+ψN,x,i+2kx,iπ

(3)

式中，ψD,x,i、ψA,x,i、ψS,x,i、ψθ,x,i和ψN,x,i依次对应形变相位、大气相位、轨道误差相位、地形误差项相位及噪声；2kx,iπ为解缠相位的模糊度，对于同一干涉图上不同PS点而言，在相位解缠精度足够高的情况下，其数值相同[15]。

形变相位ψD,x,i既空间相关，又时间相关。假设像素点的相位值可以用时间上的三次函数进行拟合

ψx(t)=a0,x+a1,xt+a2,xt2+a3,xt3

(4)

式中，a0,x和a1,x为常量和平均速率值，代表线性形变；a2,x和a3,x为加速度和加速度变化值，代表非线性形变。

由于干涉图连续生成，且重访周期固定，给定第一张SAR影像的成像时间t1=0，则第i张影像的成像时间ti为

ti=Δt·(i-1)

(5)

式中，i=1,2,…,N+1；Δt为重访周期，即时间基线。则ψD,x,i为

ψD,x,i=ψx(ti)-ψx(ti+1)=

(6)

地形误差相位ψθ,x,i是部分空间相关的，其大小与垂直基线B⊥,i成正比，可写为

ψθ,x,i=B⊥,i·θx

(7)

式中，θx为需要求解的未知参数，对于一个PS点而言，θx在所有干涉图上的值均相同。

大气相位ψA,x,i是相邻两次成像大气延迟相位之差，为空间相关但时间不相关。轨道误差相位ψS,x,i可通过Deramp处理单独估算并去除。而2kiπ则可通过选取参考点，在所有干涉图上减去参考点对应的相位值的方法而消除。

2.2 地形误差相位解算

为了消除地形误差相位对形变解算的影响，本文利用重访周期固定的特点，在干涉图之间作差分处理，在单独去除轨道误差相位后，由式(3)得

Δψx,i=ΔψD,x,i+Δψθ,x,i+ΔψA,x,i+ΔψN,x,i+2Δkx,iπ

(8)

式中，Δ表示差分运算符。则ΔψD,x,i为

ΔψD,x,i=ψD,x,i-ψD,x,i+1=

[ψx(ti)-ψx(ti+1)]-[ψx(ti+1)-ψx(ti+2)]=

2Δt2·a2,x+6Δt2·ti+1·a3,x

(9)

由式(9)可知，经过干涉图差分后，线性形变被消除，意味着对于在时间上只表现线性形变的点而言，其ΔψD,x,i为零，而对于含有非线性形变的点而言，在去除线性形变后，并随着方程阶数的降低，其数值也通常较小。

为了进一步消除其他项对地形误差解算的影响，在式(8)的基础上，对相邻PS点之间进行差分，消去2Δkx,iπ，并代入式(7)和式(9)

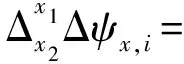
(10)

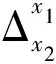
式(10)可改写为矩阵形式

Aα=δψ

(11)

式中，A为(N-1)×3的矩阵

(12)

α为3×M的矩阵，其中M为式(10)的个数

(13)

δψ为(N-1)×M的矩阵，表示差分干涉图的相位值。

这种新的地形误差解算方法利用两次差分，能避免地形误差相位解算过程中对形变相位的影响，并且通过三角网平差的方法提高解算精度，在整个解算过程中避免使用空间滤波。

2.3 形变相位解算

在去除地形误差相位后，由式(3)得

(14)

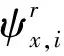
大气相位的存在仍会对形变解算精度产生较大的影响，为了消去大气相位，通过与高斯函数进行卷积运算，对相位进行时间上的低通滤波，则

(15)

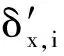
将式(15)改写为矩阵形式，为

Bv=ψ

(16)

式中，B为N×3的矩阵

(17)

v为3×K的矩阵，K表示PS点个数

(18)

式(16)同样可采用最小二乘方法求解，最终通过乘以系数λ/4π得到PS点在雷达视线(light of sight,LOS)方向的形变量。

3 试验结果与分析

3.1 连续干涉像对

本文使用的DEM为3″的SRTM数据，SAR影像数据为欧空局(ESA)Sentinel-1B降轨SLC影像，成像时间自2016年11月至2018年1月，共32幅影像。通过连续干涉像对的方法，选择20170624影像作为配准主影像，生成31幅干涉图，见表1。

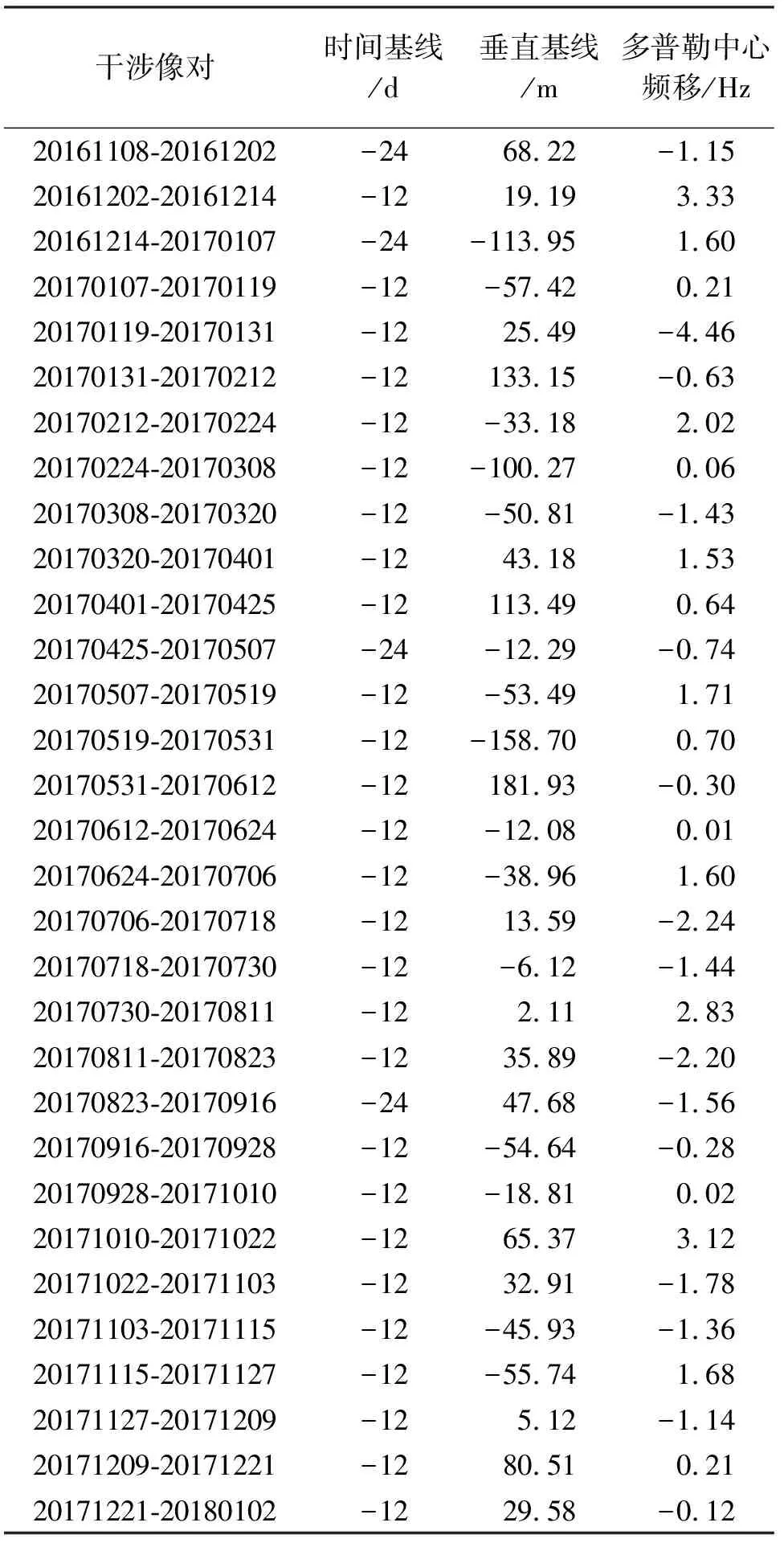
表1 连续干涉像对

表1统计了连续干涉像对的基线及多普勒中心频移，可以看出连续干涉像对的时间基线大多为12 d，垂直基线均小于200 m，相比于传统PSInSAR使用单主影像的方法，连续干涉像对方法能在保证垂直基线较短的同时，使时间基线导致的去相干最小化，具有更高的相干性(如图1所示)。

图1分别为使用连续干涉像对和单主影像干涉像对方法，对像素点在所有干涉图上平均相干性的统计。由图中可知，连续干涉像对的方法有效地提升了相干性，并且消除了单主影像干涉像对中存在像素点完全失相干的情况。

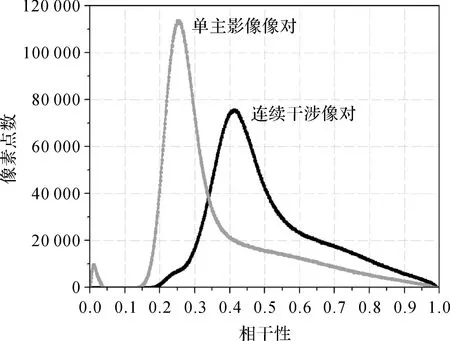
图1 像素平均相干性对比

相干性的提升也提升了PS选点的质量，图2为对PS选点过程中求解的平均相位残差的统计。由图2可知，在无需估算单主影像干涉像对存在主影像误差的情况下，绝大部分提取的PS点的相位残差在-0.1～0.1间波动，其具有较高的质量。

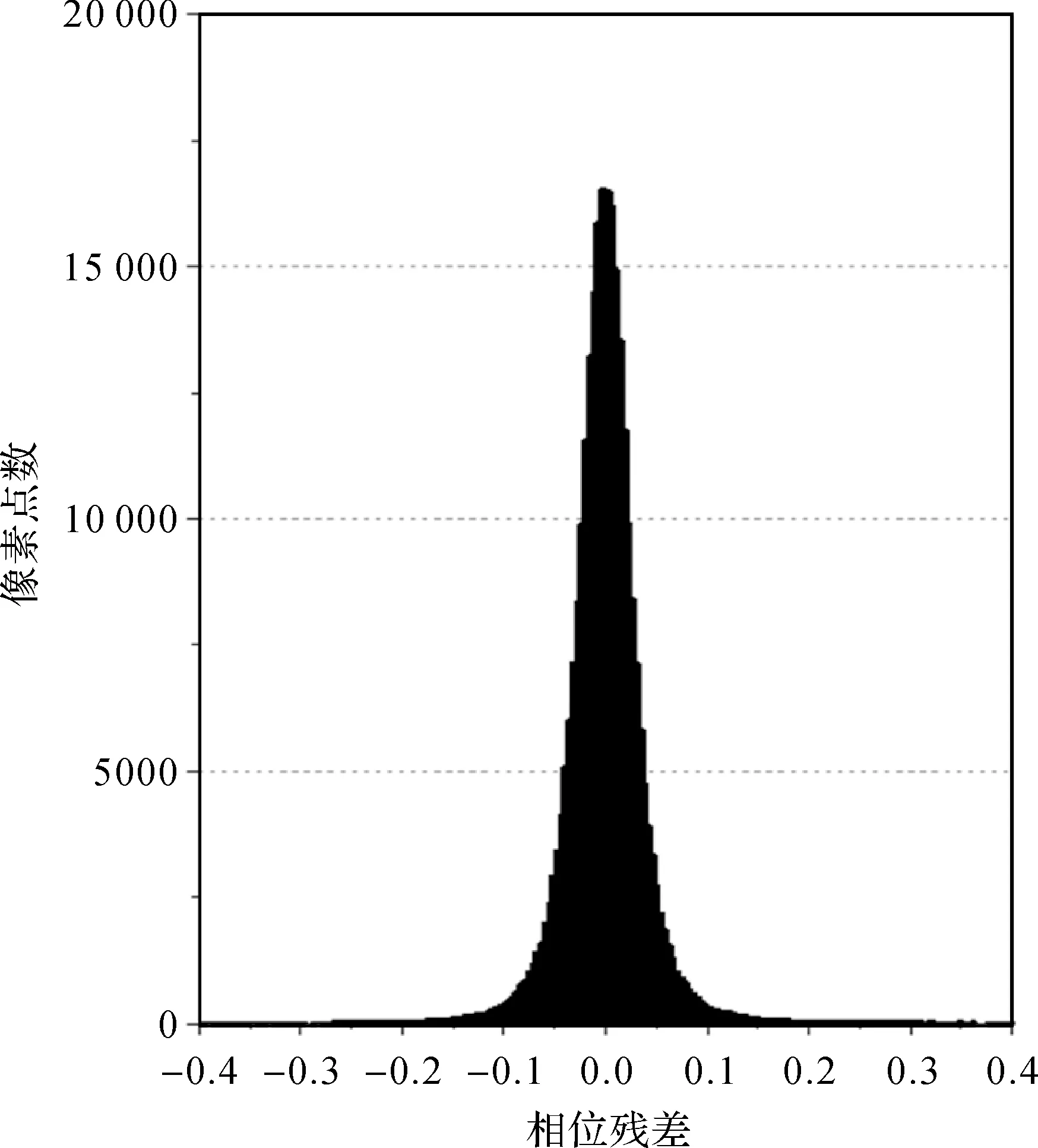
图2 PS点相位残差

3.2 地形误差相位解算

理论上采用连续干涉像对的方法，所有干涉图均应具有相同的时间基线，但由于多种因素，如雷达天线问题、紧急任务或卫星存储限制等，会存在预期的影像没有成像的情况，导致干涉图差分存在断点。本文研究从表1中选出3个连续时间段的干涉像对(20170107-20170401，20170425-20170823和20170916-20180102)，生成23张差分干涉图，对地形误差相位进行求解。

图3显示了单个PS点地形误差相位由式(11)解算的例子，由图中可以看出拟合值能较好地还原观测值的变化趋势，较精确地解算地形误差相位，证明了两次差分方法求解地形误差相位的可靠性。

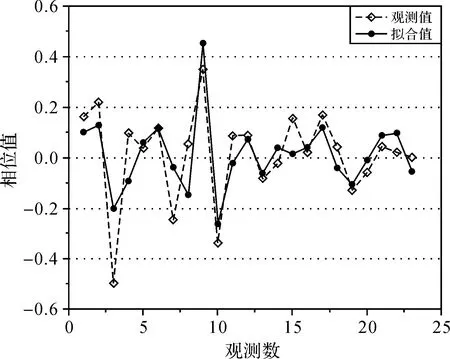
图3 地形误差相位解算

在解算出地形误差相位后，可在去除地形误差相位的基础上重新进行相位解缠，以提高解缠精度，再用改善的解缠结果重新解算地形误差相位。此步骤可重复数次直至地形误差相位解算结果不再改变。

3.3 试验结果验证

在由式(16)解算出LOS方向的形变后，通过除以入射角的余弦值将其转化为竖直方向上的形变，生成天津市的沉降速率图，如图4所示。

图4 平均沉降速率

图4中采用同时期的Landsat 8灰度影像作为底图，测量出沉降值的区域即为选取PS点的位置，标出的十字点为用于验证结果的水准点。由图4可知，PS点准确地还原了天津市的建筑、桥梁、道路及城镇的位置，测量出沉降漏斗所在的位置，清晰地显示了地面沉降在空间上的相关性。

为了验证测量结果的可靠性，将测量的结果与水准数据进行对比，水准点的位置如图4所示。本文采用克里金插值得到水准点测量值，其对比结果见表2。

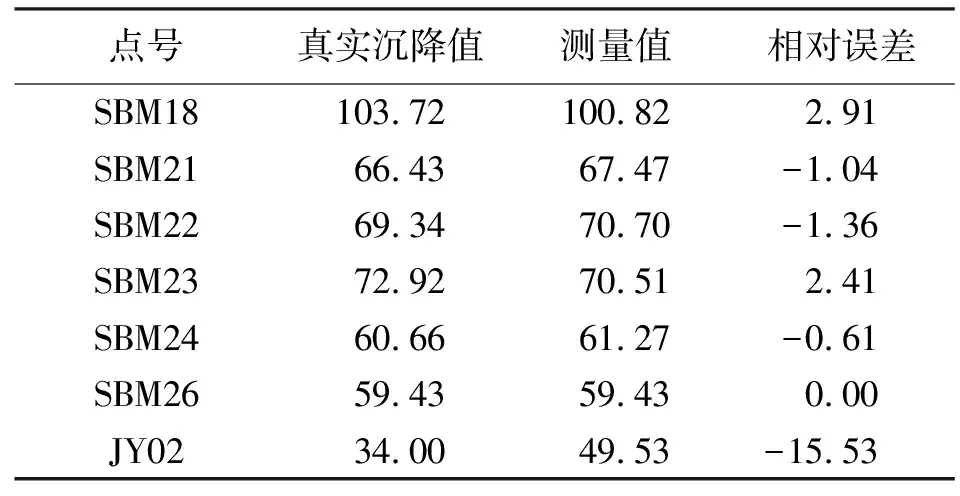
表2 试验结果对比 mm

表2中各点的真实沉降值分别为2016年11月及2017年10月测量的水准差，为绝对值，而测量值则是选择SBM26作为参考点(因此该点的相对误差为零)，由此得出的相对值。由表2可以看出，新算法整体测量精度较高，证明了新算法的可行性。

4 结 语

本文研究结合Sentinel-1数据的特点，提出了基于连续干涉像对的PSInSAR算法。相比传统单主影像干涉组合方法，新算法能够使时间导致的去相干最小化，获取更高的相干性，从理论上整体提高PSInSAR算法的精度。同时利用Sentinel-1数据具有重访周期固定的特点，通过干涉图差分去除线性形变，使用三角网平差单独求解地形误差相位，达到避免使用空间滤波、提高解算精度的目的。最终通过监测天津市的地表沉降，将测量结果与水准数据进行对比，证明了新算法在该地区的可行性，具有后续的研究价值。

致谢：感谢ESA提供的Sentinel-1数据及开源数据处理软件SNAP。