基于支持向量机的企业生产设备采购预测模型研究

谢荣燕 ，赵明

（1.河海大学商学院，江苏南京211100；2.海军航空大学，山东烟台264000）

支持向量机（Support Vector Machine，SVM），是由Vapnik提出的一种新兴的基于数据学习的机器学习技术，是最大间隔超平面、Mercer核、凸二次规划、稀疏解和松弛变量等技术的集大成者。与以人工神经网络为代表的其他机器学习技术不同的是，SVM的理论基础是统计学习理论，而不是传统的统计学理论。利用SVM进行预测的应用领域正在逐步拓展，SVM预测方法除了在工业界得以应用外，在经济金融、生物学等领域也逐渐得到应用。支持向量机是统计学习理论中最核心的部分，其在回归算法的研究方面表现出了极好的性能，尤其对小样本问题有非常好的拟合效果。支持向量机（SVM）方法根据结构风险最小化（SRM）原则，通过转化为一个凸二次规划问题来求解，能够保证得到的极值就是全局最优解，一方面可以有效地克服过学习问题，另一方面又可以防止造成维数灾难，在解决小样本学习问题上具有神经网络等方法不可比拟的优势。

1 基于支持向量机生产设备采购量预测模型基本步骤

以影响生产设备采购量发生的因素作为输入，以生产设备采购量作为输出，建立基于支持向量机生产设备采购量预测模型，其基本步骤如图1所示。

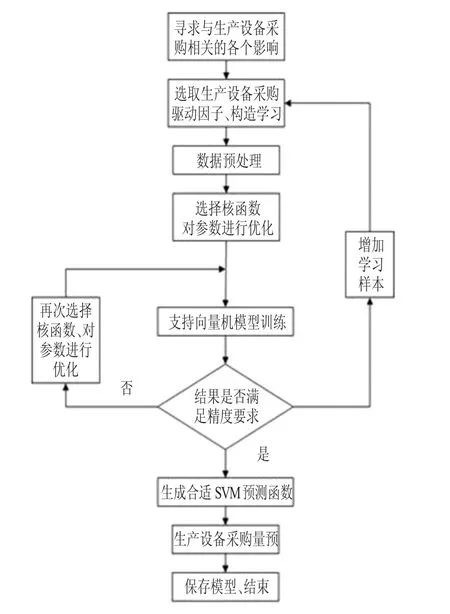
图1 支持向量机生产设备采购量预测流程

第1步，寻找与生产设备采购量相关的各个影响因素。影响生产设备采购量的因素有很多，采购量不仅与历史需求有关，而且与其他多种影响因素有关，同时各影响因素相互之间的关系比较复杂。如生产设备运转时间、生产设备综合性能、生产设备的采购的难易程度等因素，都对生产设备采购量有不同程度的影响。

第2步，生产设备采购量驱动因子（描述各个影响因素的说明性变量）的选取。生产设备采购量驱动因子的确定原则：采购量驱动因子合乎逻辑地和各个影响因素相联系；采购量驱动因子的变化引起生产设备采购量的变化具有一贯性；采购量驱动因子的量值易于确定。

第3步，对数据进行预测处理，采用支持向量机对生产设备采购量样本进行学习，生产设备采购量驱动因子是输入，生产设备采购量为输出；并对精度进行分析，若不能达到要求的精度，重新选择核函数，若达到精度要求，生成合适的SVM预测函数。

第4步，输入新的生产设备采购量情况样本或者已有生产设备采购量在不同情况下的样本，到支持向量机模型中进行生产设备采购量预测。

第6步，增添新的生产设备采购量样本到支持向量机进行学习，不断地提高生产设备采购量预测的精度。

第7步，预测生产设备采购量数据，保存模型。

2 生产设备采购量影响因素分析及量化

根据对某企业采购情况的分析研究，影响生产设备采购量的主要因素包括：生产设备运转时间、生产设备综合性能、生产设备的采购的难易程度。

（1）生产设备运转时间，运转时间越长，发生故障的概率也就越大，需要采购量增加。

（2）生产设备综合性能：制造工艺、产品质量等也会对生产设备的消耗产生重要的影响，生产设备质量越好，平均故障间隔时间越小，生产设备的需要采购量就越小。

（3）生产设备的采购的难易程度：生产设备易于采购，采购时间短，则生产设备的储备量就不用太多；反之，生产设备采购困难，采购时间长，则储备量就要相对多一些，采购量也就更高一些。

根据此原则将生产设备采购量C的主要影响因素归纳为：生产设备运转时间T、故障率Q，平均故障间隔时间M、不易采购的程度S。将影响生产设备采购的4个因素作为支持向量机的输入参数，将生产设备的采购量C作为输出。

在上述4个影响因素中，前3个指标均为数值指标，很容易量化。而对于第4个因素，可以通过查询生产设备的订货纪录结合工作人员的经验，将这一指标转化为0～1的数值指标，即极易容易采购则赋值为1，否则为0。

3 采购预测量准确度评价

对于设备采购量的预测准确度评，可以从常用的测评价方法中选取合适的指标作为评价标准。本文选用平均绝对误差（MAE，Mean Absolute Eror）、均方误差（MSE，Mean Squared Error）对采购量的预测结果进行综合评价。评价指标计算如下：

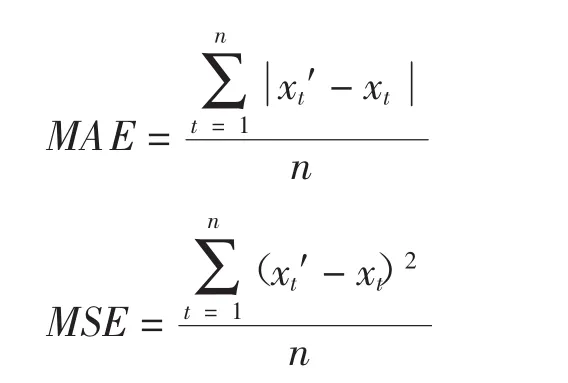
根据上述定义可知，MAE、MSE值越小，表明预测值与实际值的拟合精度越高，则需求预测的准确度越高。

4 实例分析

以年为单位，对某生产设备2000年到2009年采购影响因素的相关数据进行搜集整理，结果见表1。以前9年的数据作为训练样本，以第10年（2009年）的数据作为测试样本，应用基于支持向量机的生产设备采购模型进行采购量预测。

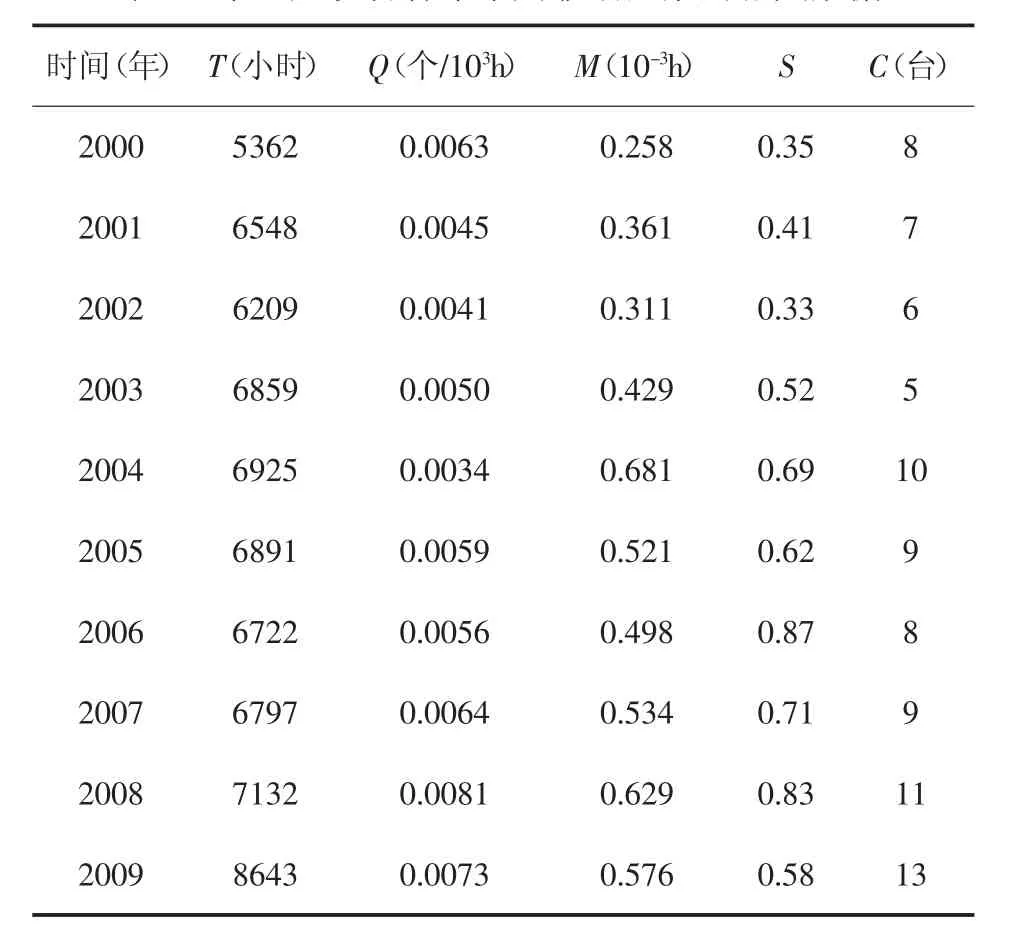
表1 某生产设备各年采购影响因素的相关数据

为了适应支持向量机的对数据的要求，减少误差，进而更加准确的进行采购量预测，采用极差变换法分别对数据按照下列步骤进行归一化处理：

（1）寻找各数据中的最大值和最小值，分别记为MAX，MIN；

（2）将第t年的数据Xi转化为：

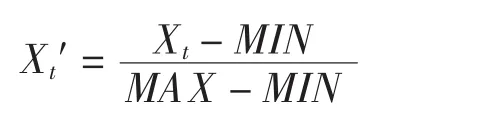
通过极差变换法，将每年影响生产设备采购量的相关数据均变为属于[0，1]区间的值。某生产设备各年采购量影响因素的相关数据经归一化处理的结果见表2。极差变换归一化处理并不改变各期数据之间的相对关系，因此，不会影响到采购量预测模型的构建。

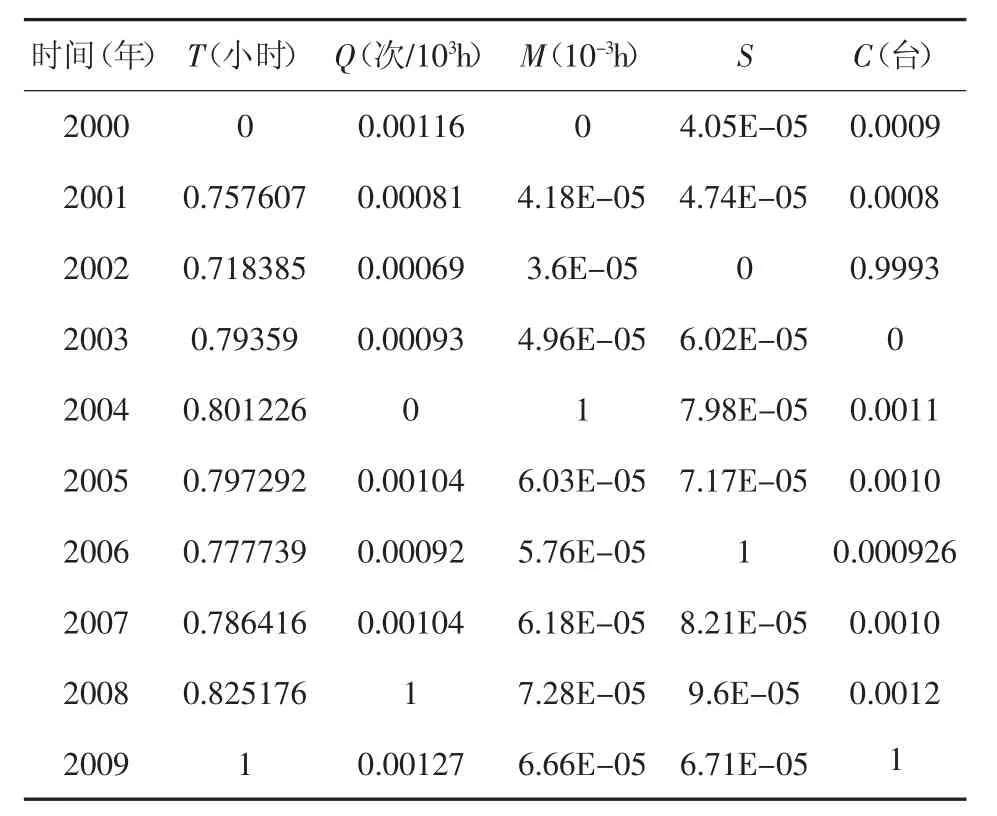
表2 归一化某生产设备各年采购量影响因素的相关数据

运用支持向量机回归原理进行该生产设备的采购量进行预测。选择RBF核函数作为核函数，因为RBF核函数只有一个g，再加上一个惩罚系数C，所以只需对这两个参数进行优化。选择网格搜索法对惩罚系数C和核参数g进行优化，参数寻优的过程如图2所示。当C=1024，g=0.0315时MSE取达到最小值，此时的（C，g）取值为最优值。

由图3可知，预测曲线与实际数据的拟合性能较好，经计算得到MAE=0.645，MSE=0.7191，2009的采购预测值为12.316。

图3 生产设备采购量预测SVM-RBF核函数

根据以上数据实验的结果与分析，对比此种方法的MAE、MSE值及2009年的采购预测值可以得出以下结论：采用RBF优化参数的支持向量机进行预测所得到的结果和实际值十分接近。利用支持向量机回归理论对生产设备采购量进行预测，方法简单，对数据的样本量要求较少，预测过程比较客观，不存在主观因素，可以高效、准确地对采购量进行预测。因此，运用支持向量机这种新兴的工具能够较好地解决小样本生产设备采购量预测问题。

5 结束语

采购工作是一个企业正常运转的一项重要内容，它与一个企业合理优化各种资源配置密切相关。生产设备作为一个企业采购的核心部心，价值大、重要性高，其采购量预测模型是企业管理理论研究的一个重要领域。一般模型在预测采购量时通常假定其服从某种概率分布，如正态分布、泊松分布等，然后通过样本数据进行参数估计和假设检验，进而得到采购预测数据。但是这类方法的理论基础是基于样本数目趋于无穷大的渐进理论。生产设备的小样本的采购特征决定其历史使用数据的样本量有限，这使得对其采购量预测的难度非常大。支持向量机是基于统计学习理论的一种新的机器学习算法，它根据有限样本信息在模型的复杂性和学习能力之间寻求最佳折衷，以期获得最好的推广能力，解决了以往学习方法中存在的小样本、非线性、过学习、高维数、局部极小等实际问题。本文将支持向量机回归原理应用到生产设备采购量预测领域，提出了基于支持向量机生产设备采购量预测的基本步骤。以实际数据为例，运用支持向量机进对生产设备采购量进行预测，验证了支持向量机预测性能的先进性。