集成学习方法研究

周钢，郭福亮

（海军工程大学电子工程学院，湖北武汉430033）

随着移动互联网以及物联网技术的不断深入应用，各类信息数据以极快速度产生和累积，大数据时代已经来临[1]。大数据备受关注，核心在于挖掘出新的有价值信息[2]。数据挖掘是从已知数据集合中发现各种模型、概要和导出值的过程和方法，也是从大数据中挖掘价值信息的核心手段[3]。

集成学习（Ensemble Learning）是一种重要的数据挖掘方法，主要利用多个学习器的集成来解决问题，能够显著提高学习系统的泛化能力[4]。Elder在文献[5]中研究表明分类器集成技术优于简单的平均法和单一模型，且在近年来多届KDD和CIKM Cup中取得优秀成绩。集成学习也被认为是未来机器学习的重要研究方向之一，是提高学习精度的重要手段[6]。

在介绍集成学习的基本概念基础上，研究了当前集成学习方法的评价标准，分析了常用的分类器集成学习算法和结果整合集成方法，对集成学习方法有综合充分了解。

1 集成学习的概念

集成学习是数据挖掘算法的一种，本质上是将多个弱分类器通过有效融合集成为一个强分类器，提高分类精度。数据挖掘包括分类，聚类，关联等多种方法[7]，集成学习主要针对分类和回归作为基分类器，两者区别主要在于预测输出值是否为离散值，本文中主要针对分类器的集成方法进行研究。

分类器是一种利用已知的观察数据（测试数据或实验数据）构建的分类模型，并以此来预测未知类别的对象所属类别。常见的基分类器包括线性回归，决策树，基于关联规则的分类，贝叶斯信念网络，向后传播，支持向量机（SVM）等方法，其中包括ID3及其改进算法C4.5，分类回归树CART，基于频繁模式的CBA、CMAR、CPAR 等算法[8，9]。

集成学习是建立基分类器的基础上进行有效融合集成形成强分类器，其中包括两个主要工作，一是基分类器的构建，二是多分类器的融合集成方法。集成学习算法的一般实现框架如图1所示。

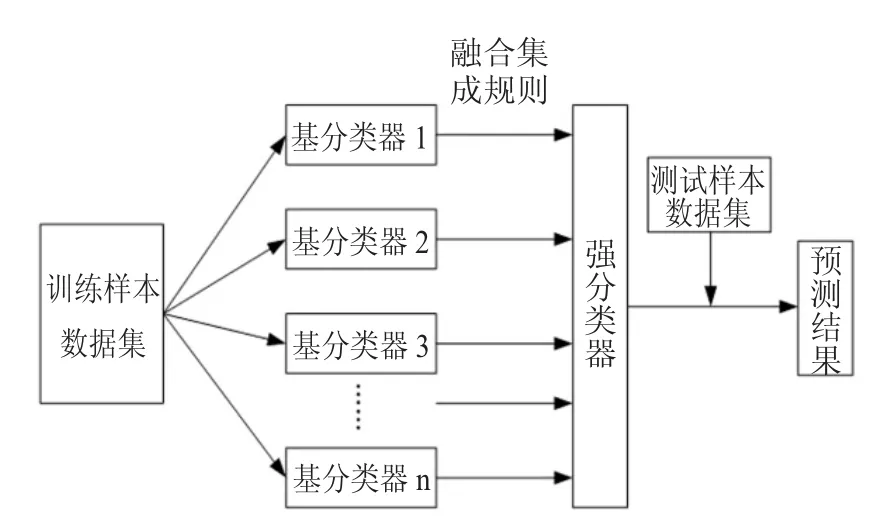
图1 构建集成学习方法的一般框架

集成学习的两个主要工作一般可以划分到训练和检验两个阶段。训练阶段是训练形成集成模型，主要针对训练样本数据集，划分多个弱分类器按照一定的融合集成规则形成一个强分类器；检验阶段是验证调整集成模型，主要针对测试样本数据集，对多个弱分类器的预测结果按照一定的集成整合规则形成集成预测结果。其中，多分类器融合的集成模型是我们研究的重点。

集成学习方法按照基分类器的类型异同可以分为同态集成学习和异态集成学习，同态集成学习包括决策树集成和人工神经网络集成等，包括同态模型的集成包括统一融合、线性融合和堆融合方式，stacking算法是堆融合的典型方法，异态集成学习包括叠加法（stacking算法）和元学习法（Meta Learning）[10]；根据基分类器的生成顺序可以分为串行组合，并行组合和混合拓扑组合，经典的集成学习方法Boosting以及其改进的AdaBoosting、GDBT（Gradient Boosting Decision Tree）都是串行组合[11]，Bagging以及在此基础上的随机森林算法则是并行组合[12]，两阶段集成学习TPEL是一种混合拓扑组合[13]；根据基分类器的学习基础分为基于数据和基于属性的集成方法，其中Bagging、AdaBoosting都是基于数据的集成方法[14]。

2 集成学习的评价标准

Dietterich在文献[4]中从统计、计算和表示三个层面阐述了集成学习的相对于单一学习器的优越性。本节重点分析集成学习模型的预测误差计算方法，并分析有效控制误差的途径。

对于单一分类器，其性能评价指标主要有训练精度、查准率、查全率、F-Measure值等[15]，集成学习方法通过对基分类器（性能较弱）通过集成融合形成强分类器，假设n个相互独立基分类器的查准率为p，那么集成学习模型的准确度为：

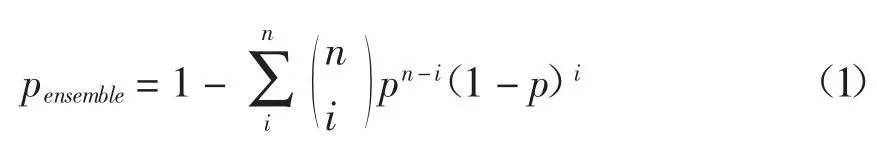
其中，第1到第i个基分类器作为样本错误检验模型。根据公式1可以发现，集成学习准确率pensemble提升的基本条件在于：一是各基分类器的相关性低；二是各基分类器的查准率p高于0.5；三是有一定数量的基分类器。因此，提升基分类器的差异化有助于提升集成学习的预测精度（MSE，Mean Squared Error）[16]。

同时，通过基分类器数量的提升，集成学习的查准率达到较高水平。当基分类器数量较大时能够在样本训练数据集上得到很高的查准率，但是会造成过拟化，降低集成模型泛化水平，即在测试样本数据上反而有较低的查准率。

因此，对于集成学习方法，一般采用偏差-方差分解分析学习方法的误差[17]。假设存在我们需要预测的目标函数为：

其中，ε为数据对象的噪声数据误差，是系统自带误差，与预测模型选择无关，一般认为服从正态分布，即 ε ～ N（0，σ2）。

对集成学习的强分类器对目标数据集的评价拟合为：

那么针对数据集D的某一个x=xi，那么在该点的误差即为：

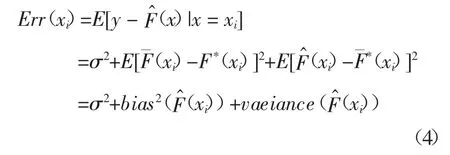
可以发现集成误差由三部分组成，第一个为系统误差；第二个为系统的平方偏差，是模型预测值与真实值的差值平方，由于预测（分类）系统中真实值无法获取，该误差是一个有用的理论概念；第三个是方差，体现了各基分类器预测值在均值周围的波动程度。

为提高预测（分类）精度，降低误差，集成学习一般在降低平方偏差和模型方差两个方面开展工作。但是，一般来说，简单模型具有高偏差和低方差，而复杂模型倾向于具有低偏差和高方差[18]。

以基分类器为决策树的集成学习为例，以集成学习的决策树数量M表征集成学习的复杂度，可以发现集成模型的预测误差与系统复杂度，以集成简单决策树数量M拟合，其相关关系如图2所示[19]。

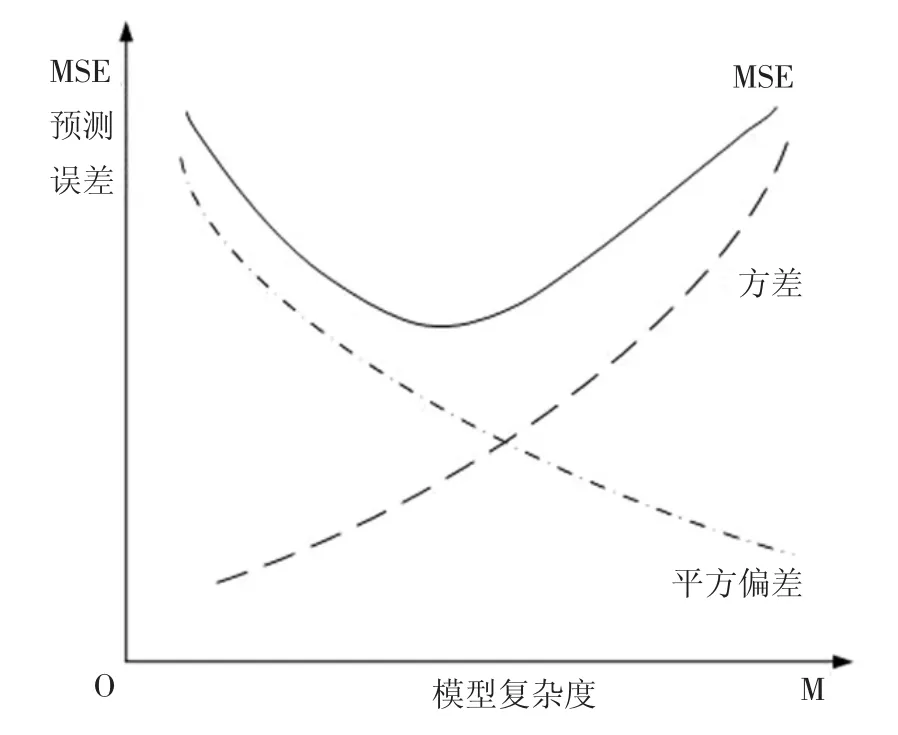
图2 预测误差（MSE）-模型复杂度关系图

根据公式1可以知道随着模型复杂度的提升，即弱分类器数量增加，集成模型的准确度即系统的偏差会降低，但同时系统间基分类器预测值间的方差将会增大，导致系统的预测误差会提升。在实际集成学习中，模型复杂度过高会导致过拟化，即模型在训练样本中有很好预测精度，在应用数据或训练样本中表现一般，如果模型复杂度过低则会导致欠拟化[20]。图3分析了集成模型在训练样本和测试样本中的预测误差。

集成学习为了降低系统的预测误差，提高预测精度，增强泛化能力，一般在控制集成模型复杂度上下功夫，主要采用正则化的方法[21]。该方法采用隐形或显性的考虑数据的有限性、不完整性和局限性，借此来构建模型的方差，借鉴了数学中解决求解反问题中的不适定问题的模型修正方法[22]。

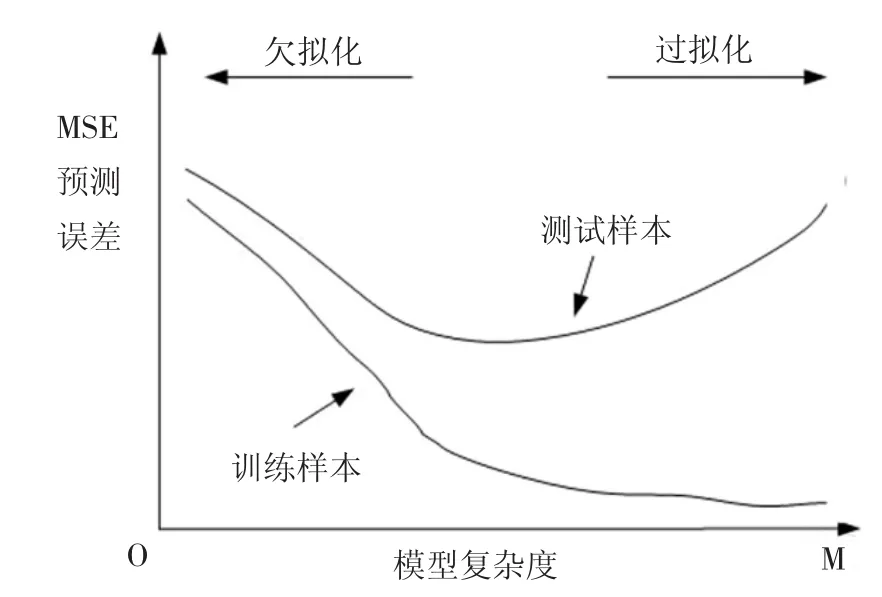
图3 预测误差-集成复杂度在训练和测试样本中区别

因此，为提高集成学习预测精度，集成学习方法在集成多个弱分类器基础上，主要从控制集成模型复杂度和提升基分类器的差异化两个方面开展研究工作。

对于控制集成模型复杂度，在分类问题中，通过属性选择或剪枝方法控制分类树的规模，典型方法如CART，同时控制基分类器数量，提升基分类器间的差异化；对于回归问题，则是通过控制参数参与度，即各参数系统比重来实现，常见方法包括约束函数，鲁棒损失函数等，典型算法如前向阶梯线性回归算法；对于提升基分类器的差异化，一般通过对训练数据集的重采样，参数设置，特征空间和引入随机扰动四个方面开展工作。

3 典型集成学习方法

集成学习方法源于1989年Kearns提出的PAC（Probably Approximately Correct）学习模型，提出了弱学习器和强学习器，进而构建了一个多项式级的学习器[23]。集成学习方法发展至今，形成了Breiman提出的Bagging（Bootstrap Aggregating）算法[24]和Robert提出的算法[25]以及在Boosting基础上 Freund和 Schapire提出了 AdaBoost（Adaptive Boosting）算法[26]。Bagging和 Boosting 算法都是基于训练数据集的重采样方法，Bagging算法是并行集成，而Boosting是串行提升，都是使用输入数据的不同训练子集和同样的学习方法生成不同模型[27]。

3.1 Bagging算法

Bagging算法是通过引导程序使用一个训练集的多个版本，即放回抽样，多每一个数据集都来训练一个不同的模型，在对训练模型通过整合输出形成一个最终的预测结果。基本算法如下。

集成预测结果hensemble（x）=f（hi（x））=y其中，y为集成预测结果，是对各基分类器Li预测结果hi（x）的整合，整合函数为f（x）。基分类器的个数N与分类种数呈正比关系。每一个Li是对训练样本T进行放回采样数据集的采用同一训练模型的基分类器。

为了控制集成学习模型复杂度，一般采用对分类决策树的属性进行筛选的方法，对不重要、不相关的分支进行裁剪。

为了提升集成模型的差异化，由于理论上每一个重抽样训练样本数据集Ti中有较高的重复率，所以Bagging算法的基分类器L一般采用不稳定算法，即调整训练样本部分的数据后，分类器Li变化较大，从而提升各基分类器的差异性。

3.2 Boosting算法

Boosting算法也是一种基于数据集重抽样算法，与Bagging算法主要区别在于需要动态调整训练样本中各数据权重，每一次迭代增加不能正确学习样本权重，降低能正确学习样本权重，从而提升在整个训练样本数据集上的学习正确率。基本算法如下。

集成预测结果hensemble（x）=f（hi（x））=y与Bagging算法不同，Boosting算法第一次构建基分类器给每一个训练数据样本赋予动态权重，加强分类错误样本权重。在下一次基分类器采用新的样本权重进行随机抽样构建新的基分类器并以此类推构建多个基分类器，并形成一个精度较高的强分类器。

为了控制集成学习模型复杂度，通过动态权重降低了高精度分类样本的权重，有效控制了最终分类器的样本数量，从而控制了集成学习模型复杂度。

为了提升集成模型的差异化，Boosting算法是一个逐步递进的方法，每一个分类器都是前一个的通过调整样本权重的改进模型。

Boosting算法问题在于更多关注不能正确分类样本数据，对于边界样本会导致权重失衡，产生“退化问题”。在Boosting基础上使用指数权重产生用于二值分类的AdaBoost算法[28，29]。

3.3 其他集成算法

随着神经网络等新机器学习方法的发展，以及着眼Bagging和Boosting系列算法的改进提升，产生了很多新的具有代表性的集成学习方法，主要算法包括神经网络集成算法，随机森林算法，选择性集成算法等。

Hansen和Salamon提出了神经网络集成方法（Neural Network Ensemble）[30]。通过使用多个基础神经网络作为基分类器对同一问题进行学习，集成分类器的输出值得到精确化的预测值。其关键点在于一是使用神经网络作为基分类器，二是对基分类器权重采用反向传播算法训练。当神经网络为单隐藏层神经网络时，构建极限学习机，并基于此开展极限学习机集成方法[31]。

2001年Breiman提出了一种用于分类预测的集成学习算法—随机森林（Random forests）[32]。随机森林算法集成多个从训练样本数据中重抽样非裁剪决策树，决策树构建中类似C4.5决策树构建方法根据增益最大挑选分裂属性，最后对每个决策树进行同权重投票实现预测结果集成。

Bagging，Boosting等算法都是对所有基分类器进行集成，文献[33]发现选择部分基分类器进行集成能够有效控制过拟化，提升集成模型泛化能力。2002年，我国学者周志华提出了“选择性集成”概念[34]，将训练得到的基分类器中精度不高，误差过大的分类器从集成模型中剔除，只选择在训练样本中表现较好的基分类器进行集成。

4 分类结果的集成整合方法

典型集成学习描述了如何通过训练样本数据得到基分类器，本节关注集成学习的检验阶段，即如何将各基分类器的预测结果进行有效整合集成形成集成学习预测结果并进行检验。基分类器的整合方式可以分为三个层次，即决策层次输出，排序层次输出和度量层次输出[35]。对于基分类器结果集成属于决策层次集成，一般包括两大类集成方法，即投票方法（Voting）和叠加方法（Stacking）[36]。

4.1 投票方法

投票方法是对各基分类器的分类结果按照某种原则进行投票表决，得到集成预测分类结果，投票方法可分为普通投票和贝叶斯投票两种。

普通投票方法可以分为均等投票和赋权投票两类，赋权投票是给投票专家赋予不同权重，均等投票则是以相同权重进行投票。根据应用背景需求，按投票原则又可以分为一票否决，一致表决，大数原则和阀值表决等[35]。对于回归问题，可以通过平均值，加权求和，中位数，最大数等方式进行整合[37]。

贝叶斯投票是根据每个基分类器的历史分类表现通过贝叶斯定理赋予不同的权重，根据各基分类器的权重进行投票[38]。由于不能覆盖各基分类器的所有样本空间，且不能正确给出各基分类器的先验概率，贝叶斯投票的效能不及普通投票方式[39]。

4.2 叠加方法

Stacking算法是1992年Worlpert提出的stacked Generalization的学习模型，对基分类器的学习结果进行再集成得到集成模型预测结果[40]。采用Leave-One-Out的交叉验证（CV，Cross Validation）方法训练基分类器，将各基分类器的训练结果作为强分类器的输入训练实例，训练学习得到最终预测结果。

Stacking算法既能集成各基分类器的训练结果，也能组合各种可能决定分类的相关信息，因此普遍认为其性能优于贝叶斯投票方法[41]。

5 总结

集成学习被认为是当前数据挖掘、机器学习中提升预测精度的重要方法。在介绍集成学习概念、评价标准的基础上，将集成学习划分为基分类器的构建和集成两个阶段，从偏差-方差分解角度，分析集成学习的预测精度主要是通过控制集成模型复杂度和各基分类器差异度实现，研究讨论了集成学习的模型构建阶段的经典算法Bagging、Boosting等，同时分析研究了分类结果集成的普通投票和Stacking方法。对于掌握集成学习的一般步骤、精度控制、经典方法以及结果集成整合等有一定帮助。