基于多传感器信息融合算法的机器人移动研究

田小静

（西安航空职业技术学院自动化工程学院，陕西西安710089）

机器人的位姿估计是移动机器人要实现自主导航的一个重要环节。移动机器人的位姿是指移动机器人的位置和姿态，需要解决移动机器人定位和姿态获取问题。

根据移动机器人定位技术和传感器的不同，机器人的位姿可通过惯性导航定位、地图匹配定位和基于信标的定位方法获得[1]。惯性导航定位利用移动机器人自带的传感器获得的信息解算出机器人的位置和姿态，这种定位需要给定移动机器人的初始位姿，定位精度高，但随着时间的推移会产生累积误差[2]，为了弥补惯性导航定位的缺陷，出现了大量的组合导航的研究[3-5]；基于地图的匹配定位是指机器人利用其自身携带的传感器建立局部环境地图，通过与已经建立的地图对比估计载体的位姿，目前对地图匹配定位的研究主要在机器人同时定位与地图构建（Simultaneous Localization and Mapping，SLAM）的问题上[6-8]，对于动态环境，SLAM 方法可能会因系统的误差增大而失效；基于信标的定位依赖环境中已知位置的信标，需在机器人上安装传感器与信标建立联系从而获得载体的位置信息，基于信标的定位有红外线、超声波、WIFI、超宽带定位等方法[9]，基于信标的定位可以获得载体的绝对位置信息，但是无法获得移动机器人可靠的偏航角，且大多数基于信标的定位方法的定位精度低，抗多径能力和穿透性差。

超宽带技术是近几年发展起来的一种新型的通信技术，其带宽到中心频率比大于0.2且信号的总带宽大于500MHz[10]。由于其非常大的带宽，其脉冲具有非常短的持续时间，所以UWB具有非常高的时间分辨率，使得UWB定位相比于其他基于信标的定位法拥有更高的室内定位精度。UWB定位系统理论上可以达到厘米级甚至更高的定位精度[11]，但是实际的室内环境往往存在遮挡，且脉冲信号易发生反射和折射，影响UWB的测距精度，从而降低了其定位精度。

针对以上单一定位方法存在的不足，提出一种用扩展卡尔曼滤波融合UWB、陀螺仪、编码器信息的定位方法，该方法既能利用UWB抑制机器人自带传感器误差的累计，同时能够提高UWB的定位精度。

1 UWB定位

1.1 飞行时间测距

飞行时间测距是通过测定UWB脉冲信号从UWB标签到UWB基站的信号往返时间从而确定其距离的，这种方法解决常规时间到达（Time of Arrival，TOA）以及时间到达差（Time Difference of Arrival，TDOA）方法中需要UWB标签与基站保持时间同步的问题。该测距原理是标签先向基站发送测距序列，其中可包含要求应答等信息，基站经过一个固定延时之后转发信号[12]，标签接收后计算一次来回程时间，标签到基站i距离di可用式（1）表示：

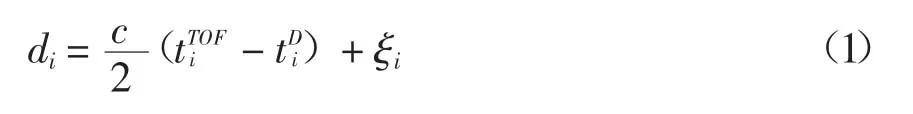
1.2 三边定位法

三边定位法[13]是一种几何法，通过测量UWB标签到多个已知位置的UWB基站的距离来估计标签的位置，该方法在目前室内定位系统中应用最广，对于二维空间定位，至少需要3个基站才能估计标签的位置。假设标签到各基站的距离分别为d1，d2，…，dn，各基站的位置分别为（x1，y1），…，（xn，yn），标签的位置为（x，y）为待求位置，可得方程组如式（2）所示。

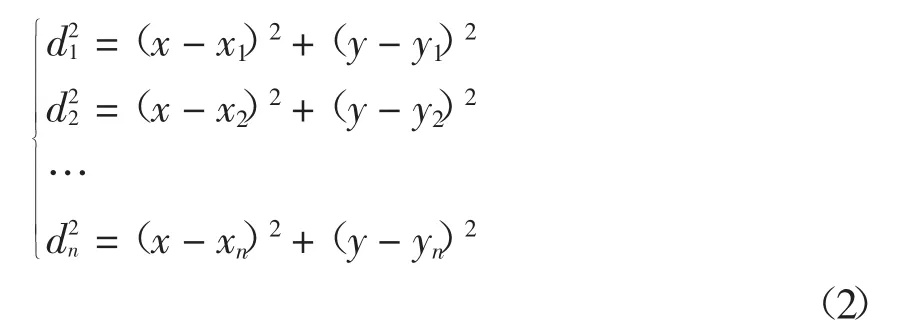
从第一个方程开始分别减去最后一个方程，得到式（3）。

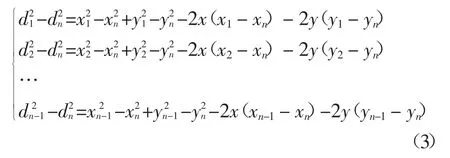
该方程组可以用式（4）的线性方程组表示：

式中，

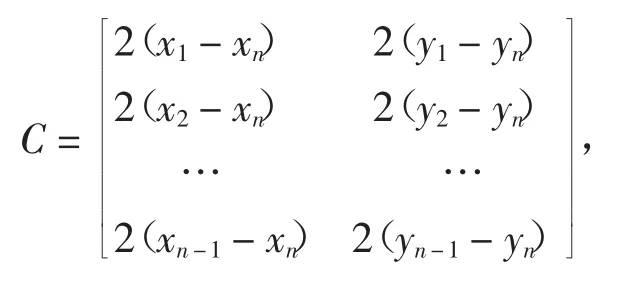
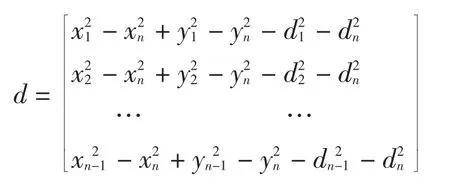
通过式（5）计算得到标签的位置。

2 移动机器人模型

移动机器人在室内环境下的模型如图1所示，在图中建立两个坐标系，XYZ坐标系为导航坐标系n系，XrYrZr为机器人坐标系b系。移动机器人通过UWB标签输出的信息获取其位置，通过陀螺仪获得其姿态，里程计可为机器人提供线速度。

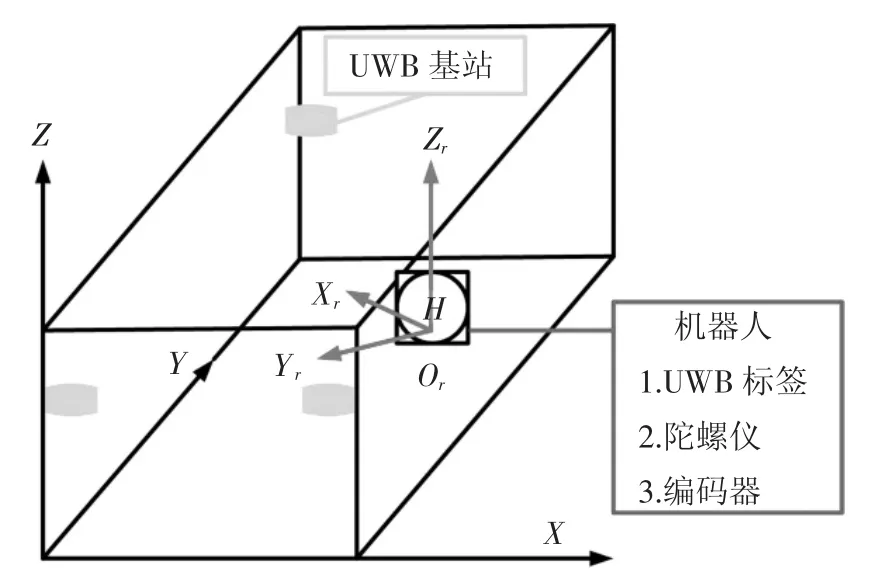
图1 室内环境下的移动机器人模型

机器人坐标系与导航坐标系的角位移关系即为机器人的姿态，可由航向角ψ、俯仰角θ和横滚角γ三个角度描述。

根据欧拉角微分方程式[14]，可以得到姿态角与角速度的关系为：

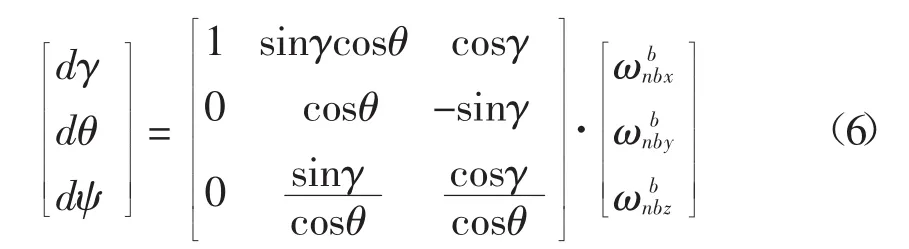
式中，

轮式机器人的线速度可通过编码器获得，设两轮轮距为L，编码器的线数为P（轮子转一圈编码器输出的脉冲数），轮径为D。通过左右编码器的脉冲频率fL和fR可以算得左右轮子的线速度为：

式中，vL和vR分别代表左边轮子的线速度和右边轮子的线速度，γ为噪声。

则机器人的线速度v可通过式（9）求得。

3 多传感器信息融合算法

3.1 系统状态方程

在二维平面中，UWB定位可以获得机器人在导航坐标系中的位置坐标（x，y），编码器可获得机器人的线速度v，陀螺仪获得机器人的偏航角速度ψ。用向量Xk描述移动机器人k时刻系统的状态：

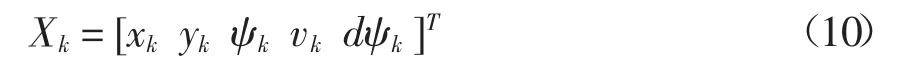
系统的状态方程为：

机器人在室内运动模型可以如图2所示的，采样周期为T，机器人在k-1时刻所在的估计位置在点pk-1处，后验估计状态为假设机器人沿着弧s在k时刻运动到位置为pk处，在pk处的先验估计状态为则弧长弧s对应的圆心为o，圆心角角度 Δψ=Tdψk-1，圆弧的半径为r=s/Δψ，直线长度 l=2rsin（Δψ/2），该直线与x轴夹角为可推导得到系统的状态方程为：

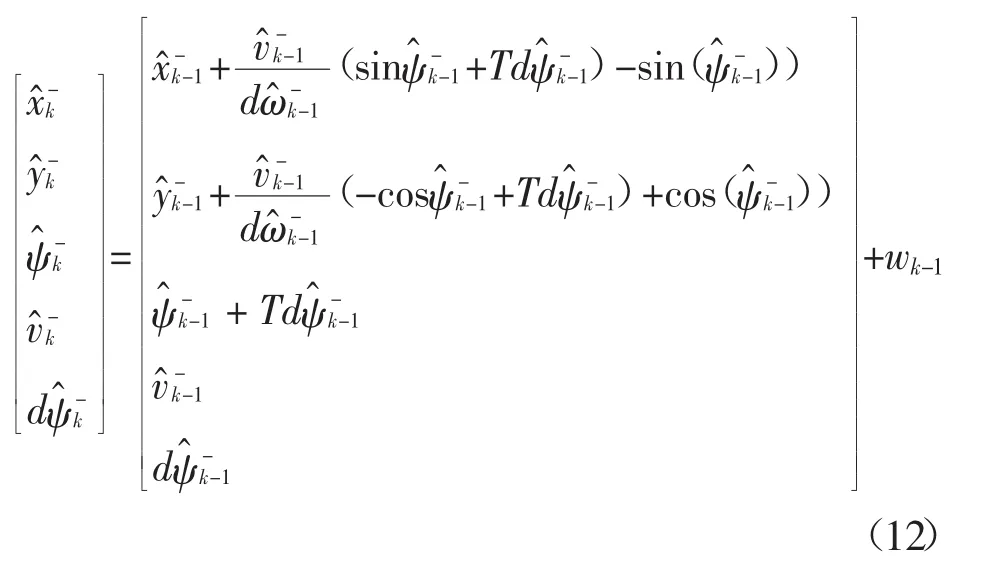
式中，wk～ N（0，Qk），Qk是k时刻过程激励噪声协方差矩阵。

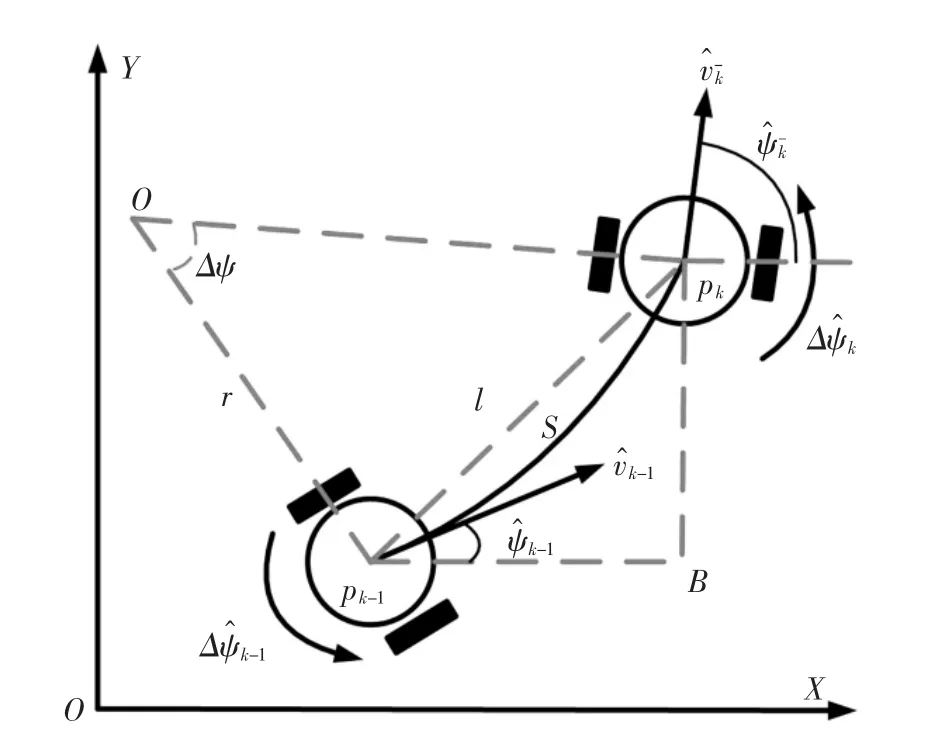
图2 移动机器人运动模型

3.2 测量方程

上面得到的状态方程是非线性的方程，需要依照扩展Kalman滤波器[15]的方式对其进行线性化和离散化处理，得到k时刻的过程雅可比矩阵如下：

扩展卡尔曼滤波时间更新过程为：

测量更新过程为：

式中，Kk是k时刻的卡尔曼增益。

4 实验与分析

4.1 实验准备

实验场所为3个UWB基站如图1所示分布在室内三个角落构成正三角形形状，UWB标签放置于移动机器人且与基站等高，实验场景如图3所示。

图3 实验场景

实验中的机器人平台为美国Willow Garage公司设计的TurtleBot2移动机器人平台，机器人里程计采用高精度增量编码器（11.7ticks/mm，25718.16ticks/revolution），采样频率为50 Hz；陀螺仪型号为STMicroelectronics生产的L3G4200D，测量范围为±250/s，采样频率为50Hz；UWB采用英国DecaWave公司的DWM1000测距模块，官方的测距精度为cm级，采样频率为33 Hz。

4.2 轨迹分析

推动机器人沿着四块地板边缘行进，四块地板的边缘的形状为长方形，该长方形长为1.72 m，宽为1.61 m。如图4到图6所示是实验过程中的轨迹图。

图4蓝色的线为单一的UWB测量得到的位置轨迹点，红色的线为机器人行进的实际轨迹，UWB测量值与实际值最大误差为0.294 m，平均误差为0.035 m，平均定位精度达到厘米级，但是在部分位置数据比较发散，单单依靠UWB进行移动机器人的定位导航还存在不足；

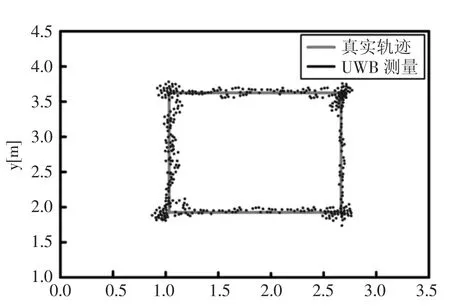
图4 UWB测量轨迹

图5蓝色的线为编码器测得的速度与陀螺仪获得的角速度进行积分获得的轨迹，从图中可以看出，该定位方法在短时间内获得比较高的定位精度，但是随着时间的增加，累计误差越来越大，轨迹越来越偏离实际的轨迹；

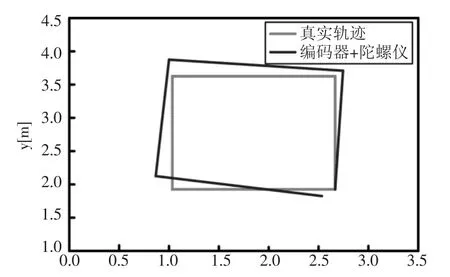
图5 编码器和陀螺仪估计轨迹

图6为运用扩展卡尔曼滤波融合UWB、编码器和陀螺仪后获得的轨迹图，可以看出，融合后的轨迹与实际的轨迹比较接近，用扩展卡尔曼滤波估计位置与实际位置的最大误差为0.058 m，平均误差为0.022 m，相比单一UWB定位，多传感器融合算法最大误差定位精度提高0.236 m，平均误差定位精度提高0.013 m。

图6 扩展卡尔曼估计轨迹

4.3 偏航角分析

机器人的偏航角是机器人位姿的重要参数，图7蓝色的线为陀螺仪测量值经过积分得到的偏航角，红色曲线为实际偏航角曲线，从图中结合表1可以看出随着实际偏航角的增大，经陀螺仪积分得到的偏航角误差越来越大；从图8可以看出，利用多传感器融合得到的偏航角没有经陀螺仪获得的偏航角稳定，但是从表1可以看出多传感器融合得到的偏航角没有随着时间的累计而增大，另外在移动机器人不知道其初始偏航角时，利用多传感信息融合可快速得到机器人的偏航角，非常适合移动机器人进行室内导航。

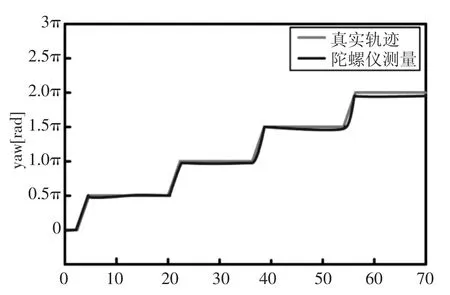
图7 陀螺仪测量偏航角

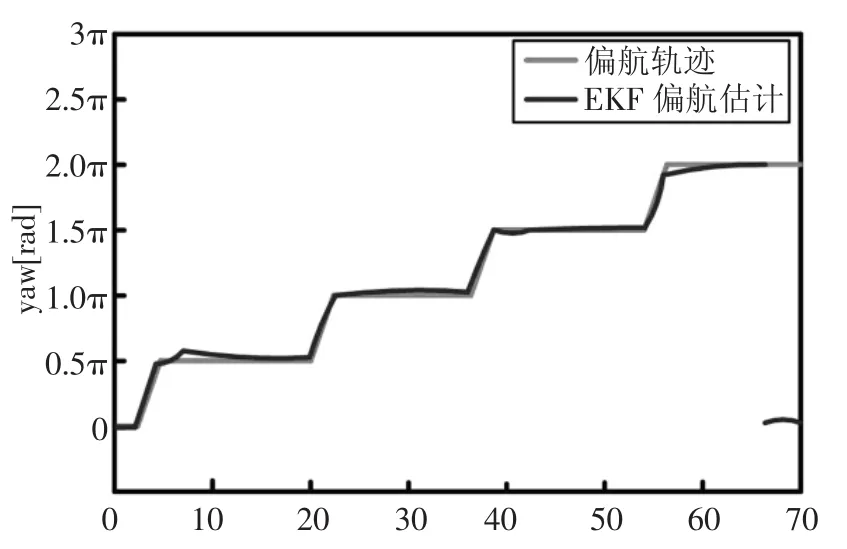
图8 多传感器融合测量偏航角

5 结论

多传感器信息融合算法可以提供移动机器人较高精度的位置和偏航角信息，针对单一定位算法存在的问题，提出一种扩展卡尔曼滤波融合UWB、陀螺仪和编码器的多传感器定位方法，该方法首先推导出融合算法的状态方程，利用UWB解算的位置和陀螺仪解算得到的机器人偏航角角速度以及编码器采集得到的机器人的线速度作为测量信息，利用扩展卡尔曼滤波获得移动机器人的位姿，并利用实验对该算法进行了验证，实验表明多传感信息融合算法能够让移动机器人获得更高的定位精度以及可靠的偏航角，为移动机器人实现自主导航做了重要的准备。