面向数据集的ST-SNE算法高维数据降维研究

董 骏

（宁夏财经职业技术学院 信息与智能工程系，宁夏银川750021）

高维数据对数据挖掘、机器学习和可视化提出了很多挑战，数据降维算法可以通过将高维数据映射到低维空间来解决这些问题。现有的数据降维方法主要分为线性和非线性降维算法[1]。线性降维算法假设低维数据分布在高维空间的线性子空间中，算法试图找到一个尽可能保存高维数据特性的线性子空间。主要的代表算法是PCA[2]和LDA[3]。由于线性降维算法具有前提条件，这类算法有其局限性，其降维效果在线性结构的数据上效果很好，但是当高维数据中包含非线性结构时，算法的效果并不理想。非线性降维算法的出现解决了这个问题。非线性降维算法的原理各不相同，较受关注的两类是基于流形[4]和基于概率[5]的算法。基于流形的算法可以保存高维空间中形成局部曲面的数据的结构[6]，从而构建一个联通的低维流形模型代表算法有 Isomap[7]、LLE[8]和 LE[9]。基于流形的算法计算量较大，且多数需要调整复杂的参数来得到合适的流形模型。在数据点分布疏密不均的情况下，这类算法可能会学习到扭曲的流形。基于概率的算法将高维空间和低维空间中数据的结构分别映射为两个概率矩阵，矩阵中的每个元素代表着两点间的近似程度。算法通过最小化代价函数来减小两个概率矩阵间的差异，最终得到数据的低维分布。这类算法的代表有：SNE[10]、t-SNE[11]和 NERV[12]等。

t-SNE的降维效果在众多降维算法中表现突出，适应范围较广。t-SNE在高维空间中使用欧氏距离来衡量数据间的相似度，但研究表明高维空间中欧氏距离并不可靠。相似度是t-SNE构建概率矩阵的先验条件，因此t-SNE展开流形的能力受到了不准确先验条件的约束。本文利用高维空间中两个数据共享的邻居信息来衡量数据之间的相似度，提出了计算高维数据间二阶邻近距离的方法，并将二阶邻近距离与t-SNE算法结合，提出基于二阶邻近距离的随机邻近嵌入算法（Second Order t-SNE，ST-SNE）。为了对算法进行评价，本文在MNIST、USPS以及COIL-20等数据集上进行了实验，对ST-SNE和t-SNE算法的降维结果进行了对比。结果表明，ST-SNE算法的降维结果提升了KNN分类的准确度，同时得到了更好的可视化效果。

1 t-SNE

t分布随机近邻嵌入算法（t-Distributed Stochastic Neighbor Embedding，t-SNE）是 Laurens于2008年提出的基于SNE的改进降维算法[13]。t-SNE将位于N维空间中的高维数据向量X1，…，Xn映射到D维空间中的低维向量Y1，…，Yn。其中yi与xi一一对应，使得低维空间中数据的分布可以反映出高维空间中数据间的关系。t-SNE的基本原理是将高维和低维空间中数据点之间的欧氏距离分别转换为两个n×n的条件概率矩阵来表示数据点间的相似性，然后最小化两个概率矩阵间的差别。

在高维空间中数据点xi与xj间的相似性被转化为pj|i：

式中，σ是高斯方差参数，它的大小与点的邻居疏密有关。pj|i是一个条件概率，如果按照以xi为中心的高斯分布来选择xi的邻居，那么xi将会以pj|i的概率选择xj作为它的邻居。若xj距离xi较近，则pj|i越大；反之，则pj|i越小。

SNE直接使用条件概率来映射数据间的相似度。但由于pi|j≠pj|i，SNE的代价函数是不对称的。为了解决这个问题，t-SNE使用联合概率分布来映射相似度，这样可以保证任取i和j，都有pij=pji。在高维空间中，t-SNE根据条件概率pi|j和pj|i计算出pij：

因此，对于所有xi有：

这保证了每个xi在代价函数中都有足够的影响力。在SNE算法中，低维映射yi与yj间的距离同样使用高斯分布映射为条件概率qj|i。但这导致了SNE算法的“拥挤问题”。“拥挤问题”是由于高维空间特性造成的，高维空间中成对距离的分布与低维非常不同。假设在10维空间中，最多有11个点可以满足两两之间距离相等，当把这11个点降到2维空间中后，这些点的关系就不可能正确的表达了。进一步考虑一个以数据点i为中心的球，其体积为r″′，其中r为半径，m为球面的维数，点i的邻居大致均匀的分布在球中。维度越高时，邻居点中处于球面附近的点的数量占总数量的比例越大。因此，当我们尝试在低维空间中对点到其邻居点的距离进行建模时，可用于映射数据点的空间与高维中的空间相比相对较小。如果想得到正确的映射点i与其邻居点的距离关系，需要将距离不同的点映射到更分散的区域。

t-SNE在低维空间中使用t分布代替高斯分布。t分布是一种长尾分布。考虑在高维空间中距离较近的两个点xi与xj。在高维空间中两点间的欧氏距离被映射为pij，为了达到pij=qij的条件，在低维空间中与会被映射的更近。同理，在高维空间中距离较远的两个点xk与xm在低维空间中就会被映射的更远。使用t分布的低维联合概率密度为qij：

t分布是高斯分布的无限混合，但是t分布的计算并不需要引入e的指数。这也使得代价函数的计算更加简洁。t-SNE算法的代价函数如下：

对称的代价函数使得梯度的计算更加简洁：

t-SNE通过使用对称的代价函数和t分布成功的改进了SNE的两个问题，得到了较好的降维可视化效果。

2 高维数据的二阶邻近距离

2.1 欧氏距离在高维空间中存在的问题

t-SNE算法在高维空间中使用欧氏距离来衡量数据间的距离。但是研究表明，在高维空间中接近度，距离和最近邻居的概念都与低维空间不同。在某些合理假设的数据分布下，高维空间中最近和最远邻居与给定目标之间距离的比率几乎为1[14]。在这种情况下，由于不同数据点的距离之间的对比度不复存在，最近邻居问题变得不再明确。文献[15]中的研究表明，对于计算距离的通式：

其中，k值越小时，所计算出的距离越适合运用在高维空间中，并由此提出了分数距离度量，即利用k＜1的距离来衡量高维空间中数据间的距离。当k=2时，式（7）代表欧氏距离。

根据本文将分数距离度量应用到t-SNE算法的实验，分数距离度量对值的选择比较敏感，当数据集的分布和维度不同时，找到合适的值需要花费较大代价。同时，使用分数距离度量对降维效果的提升有限。分数距离度量以及现有的大部分降维算法都在高维空间中直接使用一阶邻近性来度量数据间的相似性。一阶邻近性的信息并不能全面的表达数据的全局和局部结构[16]。因此，本文提出使用二阶邻近距离来度量高维数据间的相似度。

2.2 二阶邻近距离

考虑高维空间中的两点a和b，首先根据其余数据点到a和b的欧氏距离创建两个邻居列表Oa和Ob，与a或b距离越小的点在列表中的位置越靠前，图1给出了邻居列表的示例。

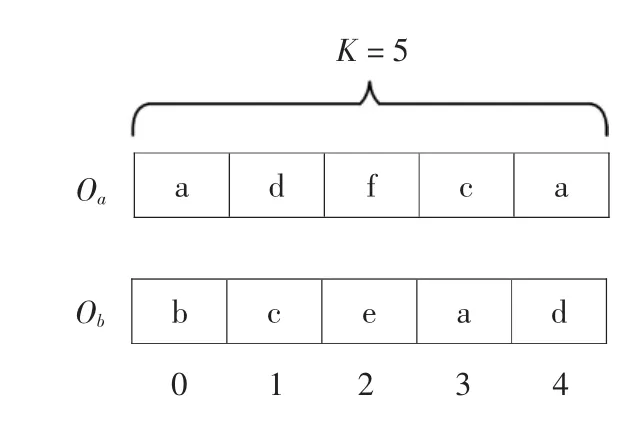
图1 邻居列表示例图

其中，K为邻居列表的长度，若数据集较小，K可以与数据点数量相同；若数据集较大，可以只取前K个邻居组成列表，以平衡算法复杂度和结果精确度。当二阶邻近距离应用于t-SNE算法时，K可与t-SNE算法中的近似参数配合。

接下来，根据邻居列表Oa和Ob计算点a到b的非对称距离 D（a，b）：

其中，1-（i/2K）为线性衰减系数，列表中位置越靠后的点对距离的贡献越小，Ia（i）返回列表Oa中位于第i位的数据点P，例如图1中Ia（0）返回点a。Rb（P）返回点P位于列表Ob中的位置，由于列表里只包含前K个最近邻居，点P有可能不存在于Ob中，故Rb（P）为：

图1 中的D（a，b）为：

同理可计算出D（b，a）。则点a与点b的对称距离D为：

本质上，D是点a与点b的邻居点在对方邻居列表中位置的加权和。D越小，则代表着点a与点b的最近邻居的结构越相似。算法实现具体描述如下：

算法1：二阶邻近距离输入：数据集 X={X1，…，xn}，邻居列表长度 K；输出：N×N的距离矩阵Ds；1.按照欧氏距离的大小计算每个数据xi的前K个邻近点，并按照由近到远的顺序组成邻居列表Oi。2.for i=1 to n 3.for j=1 to i 4. 按式（8）计算出 D（i，j）和 D（j，i）5.Ds（i，j）=Ds（j，i）=D（i，j）+D（j，i）6.end for 7.end for

3 ST-SNE

由于t-SNE使用的欧氏距离在高维空间中不能全面的表达数据集的全局和局部结构。本文在计算高维空间中数据点间的距离时使用数据的二阶邻近距离替换欧式距离。改进后的算法称为STSNE（Second Order t-SNE）。ST-SNE 基于 BH-SNE算法[17]，后者使用一定程度的近似提升了t-SNE在处理大数据集时的速度。

ST-SNE主要有三个步骤：首先计算高维空间中数据点间的二阶邻近距离并将距离转化为联合概率矩阵P，接着随机初始化低维空间中的数据分布并根据数据点间的欧氏距离生成联合概率矩阵Q，最后使用梯度下降法最小化P与Q之间的差异。

在计算二阶邻近距离时，首先要为每个数据点生成长度为K的邻居列表Oi。Oi通过在高维空间数据上构建vantage-point树并在树上进行最近邻居搜索生成，时间复杂度为O（N log N）。BH-SNE中的参数perplexity（ρ）决定了算法近似程度，在ST-SNE中规定邻居列表长度K=3ρ。根据数据集的不同，ρ的典型值为10-100，故邻居列表Oi的长度一般为30-300。这将后续计算数据点间距离的时间复杂度由 O（N2）降为了 O（KN），同时可以得到可靠的降维结果。当所有数据点的邻居列表Oi生成完毕后，即可根据式（8）计算数据点间的二阶邻近距离。

在将高维空间中的二阶邻近距离映射到联合概率矩阵P时，对于每个点只计算其与前K个邻居点的pi|j，与其余所有点的pi|j近似为0：

其中，D（xi，xj）表示点xi与xj间的二阶邻近距离。pj|i与pi|j相加计算出pij：

其中，N为数据点的总数量。使用这种方法计算pij以保证每个点在代价函数中有足够的影响力。pij最终形成联合概率矩阵p。

在低维空间中，欧式距离可以正确的表达数据的结构，所以在计算低维空间中的联合概率分布时直接使用欧氏距离，并沿用t分布将距离映射为概率：

ST-SNE同样使用Kullback-Leibler距离来最小化概率矩阵P与Q之间的差异，目标函数为：

由于KL距离的不对称性，目标函数倾向于使用大qij的值来映射大的pij。ST-SNE使用梯度下降法最小化目标函数，梯度可以整理为如下形式：

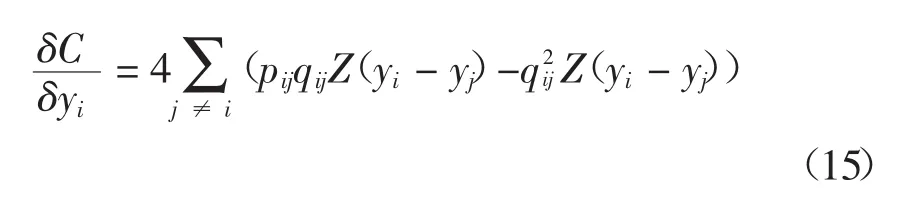
在这种情况下，当计算yj和yk两个点yi与之间的M时，yj和yk可以合并为一个点来考虑。BHSNE通过使用Barnes-Hut算法[18]来决定哪些点可以合并，ST-SNE也沿用这一做法。进行近似后计算式（16）后半部分的时间复杂度降为O（N log N）。ST-SNE算法实现具体描述如下：

算法 2：ST-SNE输入：高维数据集 X={X1，…，xn}，perplexity ρ，learning rate η，momentum α（t），最大迭代次数 T；输出：低维数据分布：；1.构建vantage-point树并进行邻近点查找，构建邻居列表；2.使用式（11）计算点i与点j间的条件概率Pj|i；3.将点i与j点间联合概率设为Pij，得到联合概率矩阵；4.在原点附近随机初始化地位分布：Y（0）={y1，…，yn}5.for t=1 to T 6.按式（13）计算低维联合概率分布7.按式（15）计算梯度8.Y（t）=Y（t）+ η δC δY + α（t）（Y（t-1）-Y（t-2））9.end for

4 实验与分析

在4个公共数据集上对ST-SNE和BH-SNE进行了对比测试，对比了两个降维算法的结果在可视化效果和KNN分类准确率两方面的表现。在实验的过程中，两个降维算法使用相同的参数和条件。下面针对每个数据集逐一进行描述。

4.1 MNIST数据集

MNIST数据集中包含了60000个灰度图片，图片的内容是手写的0-9阿拉伯数字。每张图片的分辨率为28×28=784像素，每一幅图都属于十个类别中的一类。本文直接使用像素的灰度值作为输入。在实验中，两个算法都先使用PCA将数据降维到55维，再运行各自的降维过程将数据降到2维。两个算法的perplexity参数都设置为30，在最小化目标函数的过程中都进行20000次迭代。

图2 BH-SNE与ST-SNE在MNIST数据集上的可视化对比

可视化效果对比如图2所示，其中每种颜色代表一类数据。可以观察到，两个算法都正确的将相同类别的点聚成了簇。ST-SNE不同类别之间的间隔更加明显，且相同类别的点都处于同一个簇中。而BH-SNE有些簇的边界不分明，有小部分相同类别的点形成了多个簇。

图3中展示了两个算法KNN分类准确率的结果，两个算法的表现相差不多，随着K的增大，STSNE的分类准确率更有优势。

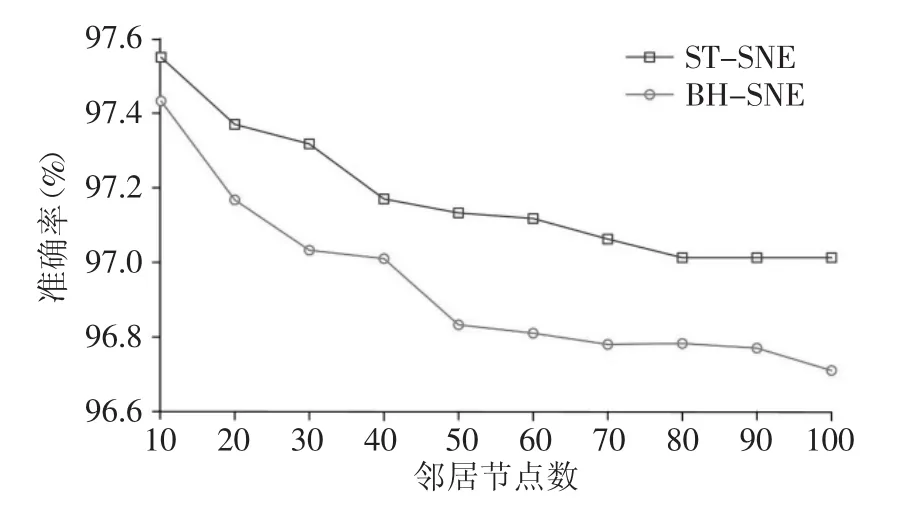
图3 BH-SNE与ST-SNE在MNIST上KNN分类准确率对比

4.2 UCI Letter Recognition数据集

UCI Letter Recognition数据集中包含20000个手写字母的数据，每个数据的维度为16维，每个数据都属于26类手写字母中的一类。由于数据维度较低，不需要使用PCA进行预处理。perplexity参数都设置为20，在最小化目标函数的过程中都进行20000次迭代。

可视化效果如图4所示。可以看到两个算法在这个数据集上表现的都不好，不能正确的把相同类别的点聚到一簇中，这主要是由于同一种字母的写法差异较大导致的。特征明显的数据大多被算法移动到了边缘，这些数据由于特征突出并一致，比较容易形成独立分隔开的簇，在这个方面ST-SNE与BH-SNE都做到了。

图4 BH-SNE与ST-SNE在UCI Letter Recognition数据集上的可视化对比

在中间的部分，数据的特征都比较模糊不易区分。ST-SNE在这部分数据中识别出了更多的特征，并形成了一些独立的簇和模糊的簇，模糊的簇在有染色的情况下是比较清晰的。BH-SNE这部分的结果显得比较杂乱，没有识别出不明显的特征。

图5中展示了两个算法KNN分类准确率的结果。在这个数据集上，ST-SNE的分类准确率高于BH-SNE，当K增大时优势更加明显。这个结果也印证了可视化结果中ST-SNE识别出了更多的特征。

4.3 USPS数据集

USPS数据集和MNIST数据集类似，数据集里包含7291个手写数字图片，图片的分辨率为16×16=256像素。每幅图片都属于0-9数字中的一类。在实验过程中，两个算法都使用PCA算法先行降维到55维。perplexity参数都设置为20，在最小化目标函数的过程中都进行20000次迭代。

图6中展示了两个算法的可视化结果，两个算法都得到了较为不错的效果，同一类别的点基本都聚集在了一个簇中。相比于BH-SNE，ST-SNE的结果中，同一类别的点聚集的更加紧密，类间的分隔更加明显。

两个算法在USPS数据集上的KNN分类准确率的结果如图7所示，两个算法的表现接近，可以看到ST-SNE的准确率在各个K值上均高于BHSNE。

图7 BH-SNE与ST-SNE在USPS上的KNN分类准确率对比

4.4 COIL-20数据集

COIL-20数据集是一个物体图片的数据集，包含20种物品的灰阶图片，共1440张图片，每张图片的分辨率为64×64=4096像素。每种物体在光照下从不同的角度拍摄72张图片。在实验过程中，先使用PCA将数据从4096维降至55维，然后分别运行两种降维算法。perplexity参数都设置为20，在最小化目标函数的过程中都进行10000次迭代。

可视化结果如图8所示，可见两个算法都很好的识别出了属于各个物体的数据并聚在了一起，在结果的局部结构中，可以清晰的观察到对于同一物体由于拍摄角度变化而形成的旋转流形。ST-SNE在这个数据集可视化结果上的表现与BH-SNE相似。

图8 BH-SNE与ST-SNE在COIL-20数据集上的可视化对比

图9展示了KNN分类准确率的结果，两个算法的准确率在值较小时相差不多，当值逐渐增大时，ST-SNE的分类准确率高于BH-SHE。

图9 BH-SNE与ST-SNE在COIL-20上KNN分类准确率对比

5 结论

提出了基于二阶邻近距离的随机近邻嵌入算法ST-SNE。二阶邻近距离在高维空间中利用邻居结构来衡量数据点间的相似度，相较于欧式距离可以更加准确的描述数据间关系。ST-SNE算法使用二阶邻近距离将高维数据结构映射为概率矩阵，解决了t-SNE中欧式距离在高维空间不可靠的问题。在MNIST等公开数据集上的对比实验结果表明，ST-SNE提升了降维结果的可视化效果和KNN分类准确率。本研究还存在一些不足：二阶邻近距离需要逐一寻找每个点在邻近点的邻居列表中的位置，时间复杂度较高；计算二阶邻近距离时，使用线性衰减来决定每个点的权重，可以研究效果更好的衰减函数；ST-SNE在更多数据集中的表现有待进一步验证。