复杂约束下的编队姿态有限时间协同控制方法

周 健，龚春林，粟 华，谷良贤

(1. 西北工业大学航天学院陕西省空天飞行器设计重点实验室，西安 710072； 2. 中国兵器工业第203研究所，西安 710065)

0 引 言

多智能体系统(Multi-agent system，MAS)编队协同控制问题是当前控制科学领域中的研究热点，广泛应用于无人机[1]、航天器[2]和水下机器人[3]等。现有文献中[4-7]，一/二阶以及高阶线性系统的协同控制问题得到了充分研究，然而针对航天器姿态系统而言，其动力学和运动学模型具有本质非线性特性[8]，使得许多针对线性MAS编队的分析方法不再适用，特别是考虑复杂约束条件下的该问题变得异常复杂。

航天器编队由于在军事侦察、深空探测、环境监测、定位服务等领域的巨大优势和广阔前景,引起了专家和学者的高度重视，是航天科技领域中的重要研究方向[9-13]。与结构复杂、功能性强的单一大型航天器相比，中小型航天器编队具有成本低、扩展性好、功能多样、可靠性高的特点，且能够完成复杂的空间任务。然而，在实际工程应用中，有些小型航天器因成本或体积结构限制无法实现对自身姿态的量测，最现实的办法就是通过设计状态观测器或者输出反馈控制器进行在线估计[14-15]。另一方面，当系统状态不可量测与参数不确定性[16]、饱和控制[17]、外部扰动、有限时间控制[18]等因素耦合在一起时，就使得航天器编队姿态协同控制问题变得极富挑战性。因此，在复杂约束条件下如何设计高精度和强鲁棒性的协同控制律[19-20]仍然是当前编队协同控制研究的重点和难点问题。

本文首先建立了航天器相对姿态协同控制模型；在此基础上，针对编队姿态控制系统存在无角速度量测、外部扰动等约束条件，提出了一种有限时间姿态协同控制律；而后将该控制律推广到更为复杂的约束条件下，通过将饱和输入影响转化为复合扰动，提出一种基于有限时间状态观测器估计的滑模姿态协同控制律，实现航天器编队在复杂约束条件下的姿态协同控制。

1 问题描述

假设由n个航天器组成的编队协同，其中编队成员的姿态运动学和动力学方程表示如下[21]：

(1)

式中:Ji∈R3×3代表第i个航天器的转动惯量矩阵，ui∈R3×3为控制力矩，di∈R3×3为外部扰动力矩，ωi∈R3×3为刚体本体坐标系下第i个航天器的角速度，qi∈R3×3表示描述航天器姿态的修正罗德里格斯参数，其定义为：

式中:ρi和φi分别代表第i个航天器的欧拉轴和欧拉角。符号×表示斜对称矩阵运算，其定义为：

(2)

式中:Ei∈R3×3为雅克比矩阵[22]。

根据上面定义，式(1)可以转换为：

(3)

且满足以下假设：

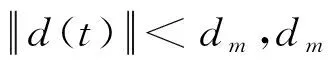
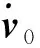
其中，c0是给定的正数。

2 有限时间滑模姿态控制协议

2.1 姿态误差追踪系统

为了便于后续分析，这里引入两类中间变量：绝对姿态误差和相对姿态误差。其中绝对姿态误差指第i个航天器与期望状态的差值，定义如下：

将上述方程代入到姿态动力学系统(3)，得到姿态追踪误差系统：

(4)

将式(4)写成向量形式：

(5)

式中:

另一方面，姿态相对误差定义为：

(6)

此外，令αi1,αi2,αi3∈R3为第i个航天器的耦合追踪误差，定义如下：

式中:aij为编队权重连接矩阵A的元素。

注意到：

式中:lij为Laplacian矩阵L的元素。

耦合追踪误差αi1,αi2和αi3可写成如下形式：

(7)

式(7)可写成向量形式：

(8)

式中:

M=(L+B)⊗I3∈R3n×3n,B=diag(b1,…,bn)

(9)

引入滑模变量si=δαi1+αi2，其中δ为正值。对变量si两侧求导：

(10)

将式(10)写成向量形式：

(11)

2.2 控制协议设计及稳定性分析

基于上述滑模变量，提出如下分布式滑模姿态控制协议：

(12)

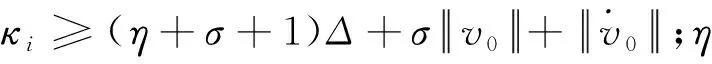
由上述定义很容易得出，鲁棒控制项ψi满足如下不等式：

(13)

在给出稳定性条件之前，引入一滑模观测器来估计未知量。

(14)

上述滑模观测器的有限时间估计性质可由下面的性质给出。

这里，Δ为任意给定的正数。

以下定理给出了滑模姿态控制律(12)的稳定性。

定理1.考虑非线性观测器(14)和滑模姿态控制律(12)，当系统满足假设1时，滑模变量s在有限时间内收敛到有界域内。

证.考虑如下Lyapunov函数：

(15)

沿着式(11)对Lyapunov函数两侧求导可得：

(16)

另一方面，系统非线性项fi满足：

(17)

式中：

上述不等式可写成下面两种形式：

(18)

(19)

对于方程(18)，当条件c1-c2/V>0成立时，系统可在有限时间T2a内实现稳定，即Lyapunov函数在有限时间内满足V≤c3/c1。那么，滑模变量s也将收敛到有界域内：

(20)

对于方程(19)，当条件满足c2-c3/V(1+α)/2>0成立时，系统可在有限时间T2b实现稳定，即Lyapunov函数满足V≤(c3/c2)2/(1+α)。那么，滑模变量s将在有限时间内收敛到有界域内：

(21)

结论得证。

3 饱和输入条件下的控制协议

本文针对编队追踪姿态控制系统(1)提出了考虑饱和输入的有限时间姿态协同控制协议。系统饱和输入控制器如下所示：

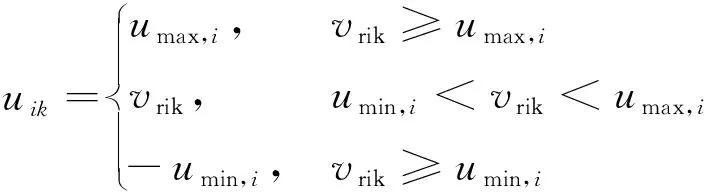
(22)

式中:vrik为控制输入量；umax,i和umin,i分别为未知的饱和控制器上下界参数，且有umin,i≠umax,i。

考虑未知非对称饱和控制器的影响，姿态控制方程(1)可写成如下形式：

(23)

(24)

考虑方程(24)和(5)，得到：

(25)

为了有效估计复合扰动Di，将文献[25]中的有限时间观测器修正为：

(26)

(27)

这里，0<α<1,ki1,ki2>0。

基于上述设计分析，饱和输入条件下编队姿态追踪控制系统的收敛性能可由以下定理给出。

定理2.对于编队追踪姿态控制系统(1)，考虑受到外部扰动、饱和输入以及角速度不可量测等约束条件的影响，有限时间状态观测器形如式(26)，则在滑模控制协议(27)的作用下，编队姿态追踪误差将在有限时间内收敛到有界域内。

证.参考文献[25]的定理1。

对于式(1)，饱和输入的影响被转化成复合扰动的一部分，并通过有限时间状态观测器(26)估计。至此，将问题转化为受到外部扰动条件下的姿态追踪系统的稳定性问题。

4 仿真校验

选取六个航天器和一个虚拟领航者组成的编队姿控系统，其通信拓扑如图1所示。

编队的权重连接矩阵A和B定义如下：

参考文献[26],假如航天器惯性矩阵取值为：

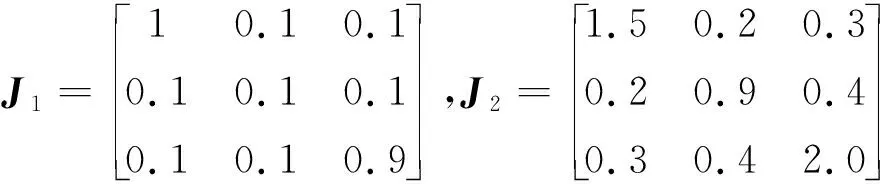
航天器初始状态(角度和角速度)取值如下：

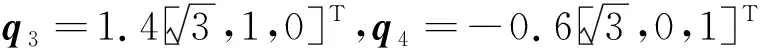
假设编队领航者期望姿态为：

假定各航天器控制器控制参数均相同：

umin,i=5,umax,i=10,ki=2
α1=0.8,α2=0.6,α3=0.4
β1=1.25,β2=1.05,β3=0.65

仿真结果如图2、图8所示。图2为控制输入曲线随时间的变化情况。图3、图4为角速度和滑模变量随时间的变化曲线。图5、图6为角速度和姿态的观测误差随时间的变化曲线。图7、图8为角速度和姿态的跟踪误差随时间的变化曲线。由图2～8可知，各航天器姿态在有限时间内趋近于期望姿态附近，因此可实现复杂约束条件下的编队姿态协同控制。

5 结 论

本文研究了复杂约束条件下的航天器编队姿态有限时间协同控制问题，提出了一种有限时间状态观测器；基于观测器输出设计了滑模姿态协同控制律，并通过Lyapunov函数证明了控制器的有限时间稳定性；针对存在饱和输入条件下的姿态协同控制问题进一步研究，将饱和输入影响转化为复合扰动，以利用前述方法进行姿态协同控制；最后通过数值仿真校验了控制器的有效性。结果表明，本文所设计的控制器能够满足姿态有限时间协同要求，且支持更为复杂的约束条件，有效地拓展了其应用范围。