着陆姿态不确定下的着陆器缓冲机构优化设计

吴宏宇，王春洁，丁宗茂，丁建中，董 洋，满剑锋

(1. 北京航空航天大学机械工程及自动化学院，北京 100083； 2. 北京航空航天大学虚拟现实技术与系统国家重点实验室，北京 100083;3. 清华大学机械工程系, 北京 100084)

0 引 言

随着科学技术的进步，人类的研究空间已不再局限于地球，探索月球、火星、乃至距地球更远星球上的奥秘已成为当今科学界的研究热点之一。而探测任务中，将机器人或宇航员安全送往外星球表面是探测任务的关键环节[1]。纵观世界各国的深空探测任务，常用腿式着陆器搭载探测设备软着陆外星球表面，如美国的阿波罗号载人登月舱、海盗2号火星探测器、凤凰号火星探测器及中国的嫦娥三号月球探测器等。腿式着陆器作为一种简单、可靠的着陆缓冲装置，需要持续开展其研究工作，而研究工作的重点内容包括着陆器软着陆过程的动力学仿真与着陆器的性能优化。

关于腿式着陆器软着陆过程仿真计算与性能优化的研究，已有较多学者开展了相关的工作。针对软着陆过程仿真分析的研究，文献[2-6]利用多体动力学分析软件ADAMS建立了腿式着陆器软着陆过程的动力学仿真模型，分析了着陆器在典型工况下的软着陆性能，其中文献[5-6]通过对比仿真结果与试验数据证明了建模方法的合理性；文献[7]基于基本力学原理，研究了着陆器冲击动力学相似性技术，提出了等效低重力工况的新方法，并利用物理样机试验验证了方法的有效性；文献[8-10]基于Monte Carlo法研究了不确定着陆工况下的月球和火星着陆器的软着陆性能；文献[11-12]则考虑多种工况因子，重点针对腿式着陆器的抗翻倒能力与载荷缓冲性能绘制了稳定性边界；文献[13-14]建立了腿式着陆器软着陆过程的动力学方程，并对方程进行求解，研究了影响着陆器软着陆性能的关键因素。针对腿式着陆器优化设计的研究，文献[15]基于响应面法与单一恶劣着陆工况，优化了月球着陆器的缓冲机构；文献[16]同时考虑多组恶劣着陆工况，直接利用动力学仿真模型参与优化迭代计算，优化了某型着陆器的缓冲机构；文献[17]除考虑多组恶劣着陆工况外，同时考虑某型着陆器的两种着陆模式，结合响应面法对某型着陆器的缓冲机构进行了优化设计。

上述研究的集中点在于腿式着陆器软着陆过程的仿真方法与特殊工况下的着陆器性能优化方法，但鲜有文章报道着陆姿态不确定条件下的着陆器优化方法。由于控制延迟、误差等原因，着陆器与星球表面接触时姿态具有随机性，故而将着陆姿态的不确定性引入着陆器的优化设计过程中非常必要。本文结合响应面法与分级优化设计方法，以某型着陆器为例，重点研究了不确定着陆姿态下的着陆器缓冲机构优化方法。

1 着陆器仿真模型建立

本文以图1所示的某型着陆器为研究对象，着陆器由主体和四套完全相同的缓冲机构组成。缓冲机构均匀分布在主体四周，由主支柱、辅助支柱、足垫和缓冲杆组成，辅助支柱内外筒间装有吸收冲击能量的缓冲元件[16-17]。

采用ADAMS软件建立非0高度关机[17]软着陆模式下的着陆器软着陆过程仿真模型，模型从着陆器与星球表面接触瞬间开始进行仿真分析，且各构件均简化为刚体或利用刚体等效建模。

考虑大变形构件缓冲杆主要通过弯曲变形的方式缓冲载荷，其等效建模方式如图2所示。首先，建立两段轴线共线的刚体，其质量特性参考真实缓冲杆赋予。刚体1利用万向节副与主体在O点联接，并限制刚体2只能沿轴线移动。缓冲杆最初状态时，轴线重合于X轴，当其末端受力导致其弯曲时，则等效于O点产生反作用弯矩M，将M投影在Y与Z轴上，得到两个弯矩分量MY,MZ。反之，在O点处对刚体1施加两个弯矩分量MY,MZ可以合成弯矩M。同时，为了模拟末端位置的变化，在刚体2上施加运动S。结合图2可知，M,S均为O点与末端连线同X轴夹角α的函数。利用测量函数，求得缓冲杆末端相对于O点的坐标(x,y,z)，进而可得α的表达式如式(1)所示，并可得到M,S的表达式如式(2)和式(3)所示。

(1)

M=f(α)

(2)

S=g(α)

(3)

建立缓冲杆的有限元模型，末端施加弯矩，可仿真计算得到α-M，α-S函数关系f，g如图3、图4所示。

仅考虑受弯，缓冲杆的俯视图为一条线段，如图5所示。结合图5，根据几何关系，可计算出M在Y轴、Z轴的分量MY，MZ的表达式如式(4)、式(5)所示。

(4)

(5)

进而，利用式(3)～(5)结合图2所示的等效模型可模拟缓冲杆的受力弯曲情况。

辅助支柱内缓冲元件的吸能过程通过在内外筒之间施加与压缩行程D相关的缓冲力FD来模拟，FD与D的函数关系如图6所示。

足垫和星球表面之间的垂向力和法向力分别采用非线性阻尼弹簧模型和库伦摩擦模型来模拟[4,16]。

2 着陆工况参数及软着陆性能判据

2.1 着陆工况参数

设着陆器与星球表面接触瞬间的整机质量为800 kg，竖直速度vx为3.7 m/s、水平速度与三轴角速度为0，星球表面的坡度为10°、动摩擦系数为0.4[9,17]，不考虑着陆器足垫撞击岩石或落入凹坑，此时着陆工况参数主要为着陆器的姿态角，而通过调整俯仰角θf与偏航角θp即可获得评判第2.1节提出的软着陆性能所需的着陆工况。考虑着陆器整机的对称性，设定θf与θp的取值范围如表1所示。

表1 着陆姿态角取值范围Table 1 Range of parameters of landing attitude angle

θf与θp的几何含义如图7所示，图中xM，yM，zM表示着陆器的机械坐标系。

2.2 软着陆性能判据

本文主要针对着陆器的软着陆稳定性，提出以下三点软着陆性能判据：

1)着陆器抗翻倒能力判据。定义包含着陆器任意相邻两足垫中心点的竖直平面为翻倒平面，着陆器的抗翻倒能力与着陆器在着陆过程质心距翻倒平面的最小距离LD成正相关，且LD应始终大于0，否则认为着陆器翻倒[18]。

2)辅助支柱缓冲行程约束判据。考虑辅助支柱内部缓冲元件的承载能力有限，需要保证辅助支柱在正常工作状态下的最大缓冲行程DM不大于80 mm。

3)着陆器底面抗损坏能力判据。着陆器的底面抗损坏能力与着陆器尾喷管底面中心点在着陆过程中距星球表面的最小距离HM成正相关，且HM过小不利于探测车的释放，在此约束HM不小于350 mm。

3 着陆器软着陆性能分析与缓冲机构优化

3.1 不确定着陆姿态下的软着陆性能分析

本文基于ADAMS模型，采用Monte Carlo法分析着陆器在不确定着陆姿态下的软着陆性能，且认为各种着陆姿态对软着陆性能的影响同等重要。首先利用描述性采样方法在表1所示的姿态角取值范围内等概率抽取样本点，之后将样本点代入仿真模型进行仿真计算，最后对仿真模型输出结果进行统计，以定量分析着陆器的软着陆性能。本文抽取2000个样本点进行仿真分析，根据2000组仿真结果绘制性能指标值的散点图如图8所示，并得到表2所示的软着陆性能分析结果。

图8中，方形散点表示HM小于350 mm的样本点。

表2 Monte Carlo模拟分析结果Table 2 Analysis results of Monte Carlo simulation

分析结果显示，着陆器底面抗损坏能力不理想，有必要对着陆器进行优化设计以提升其软着陆性能。

3.2 缓冲机构优化设计

3.2.1优化设计变量

为保证着陆器在运载火箭中的安装要求，辅助支柱与主体的连接点位置、主支柱与缓冲杆的连接点位置、辅助支柱与主支柱的连接点相对于足垫的位置均难以调整[17]。由缓冲机构构型可知，着陆器足垫的中心点至主体中轴线的水平距离dz、主支柱长度LM与辅助支柱缓冲元件的缓冲力大小可作为优化设计变量。dz，LM的几何表示如图9所示，缓冲元件缓冲力的大小利用其增减倍数kz来表达。

结合图9，可直接分析出dz，LM和kz对着陆器软着陆性能有以下三方面的影响：

1)在其他两个参数不变的前提下，dz的增加会直接加大质心距翻倒平面的初值，减小主体的高度，故dz与着陆器的抗翻倒能力成正相关、与底面抗损坏能力成负相关。

2)在其他两个参数不变的前提下，LM的增加会直接提升着陆器主体的高度，故dz与着陆器底面抗损坏能力成正相关，而主体提高的同时着陆器质心势必增高，故LM的增加会间接导致着陆器抗翻倒能力下降。

在其他两个参数不变的前提下，kz的增加会直接导致辅助支柱缓冲行程与主体下降距离减小，不难得知kz与着陆器的抗翻倒能力和辅助支柱最大缓冲行程成负相关、与底面抗损坏能力成正相关。

dz，LM和kz的初值与范围如表3所示。

表3 设计变量范围及初值Table 3 Initial values and range of design variable

3.2.2响应面代理模型

考虑结合Monte Carlo法，使用ADAMS模型参与缓冲机构的优化迭代计算效率极低。对此，本文基于响应面方法建立LD，DM，HM与dz，LM，kz，θf，θp的映射关系，响应面模型的引入将大幅度提高优化计算效率。本文采用二阶多项式建立响应面模型，包含dz，LM，kz，θf，θp五个参数的二阶多项式表达式：

φ=β0+β1dz+β2LM+β3kz+β4θf+β5θp+

β12dzkz+β13dzθf+β14dzθp+β15LMkz+β16LMθf+

β17LMθp+β18kzθf+β19kzθp+β20θfθp

(6)

式中：φ表示LD，DM，HM中任意一项的近似函数、βi表示多项式的各项系数。根据文献[19]，利用最小二乘法确定βi的取值，进而可得响应面模型的具体表达式。

本文根据均方根相对误差值RMSE和决定系数R2来判断响应面模型的拟合精度，对应表达式如式(7)、式(8)所示[19]。

(7)

(8)

利用优化拉丁超立方实验设计在表1和表3中的着陆姿态与缓冲机构构型参数范围内抽取30个样本点，利用ADAMS模型计算出30组LD,DM,HM值如表4所示，进而利用以上30组数据拟合响应面模型。

为避免多项式项数过多引起的多项式摆动等误差源，本文引入了响应面模型关键项筛选策略，即对响应面模型的多项式进行逐项筛选，保留10项来拟合样本点，选取RMSE最小的项组合方式来确定响应面模型的最终表达式如式(9)～式(11)所示。

2.732θpLM-121.739dzkz+1148.830dzLM

(9)

0.685θpLM-120.259dzkz+205.839dzLM

(10)

HM= -21936.723+23353.525dz+13572.952LM-

0.0345θfθp+2.612θfLM+402.763dzkz-

183.107kzLM

(11)

利用RMSE和R2分析响应面模型对30组样本点的拟合精度，分析结果如表5所示。

Dynamic Analysis of Semi-type Floating Offshore Wind Turbine with Failure Conditions Under Metocean Conditions in South China Sea SHI Wei,ZHENG Kan,REN Nianxin (12)

检验结果显示响应面模型可准确描述LD，DM，HM与dz，LM，kz，θf，θp的映射关系。

3.2.3优化数学模型的建立及求解

上文的分析结果显示，着陆器在初始构型参数下的底面抗损坏能力不理想，故本节将提出优化方法计算dz，LM和kz的最佳取值，以提升着陆器的软着陆性能。为使各种着陆姿态在优化过程中起同等重要的作用以保证优化结果的稳健性，本文以最大化不确定着陆姿态下LD与HM的平均值LD-ave与HM-ave为目标，以不确定着陆姿态下DM最大值DM-max与HM的最小值HM-min不超过许用值作为约束条件建立优化数学模型，为了防止优化后DM-max与HM-min与许用边界重合，优化过程中将DM许用值降为75 mm,HM许用值提升为360 mm。综上，得到优化数学模型如式(12)所示。

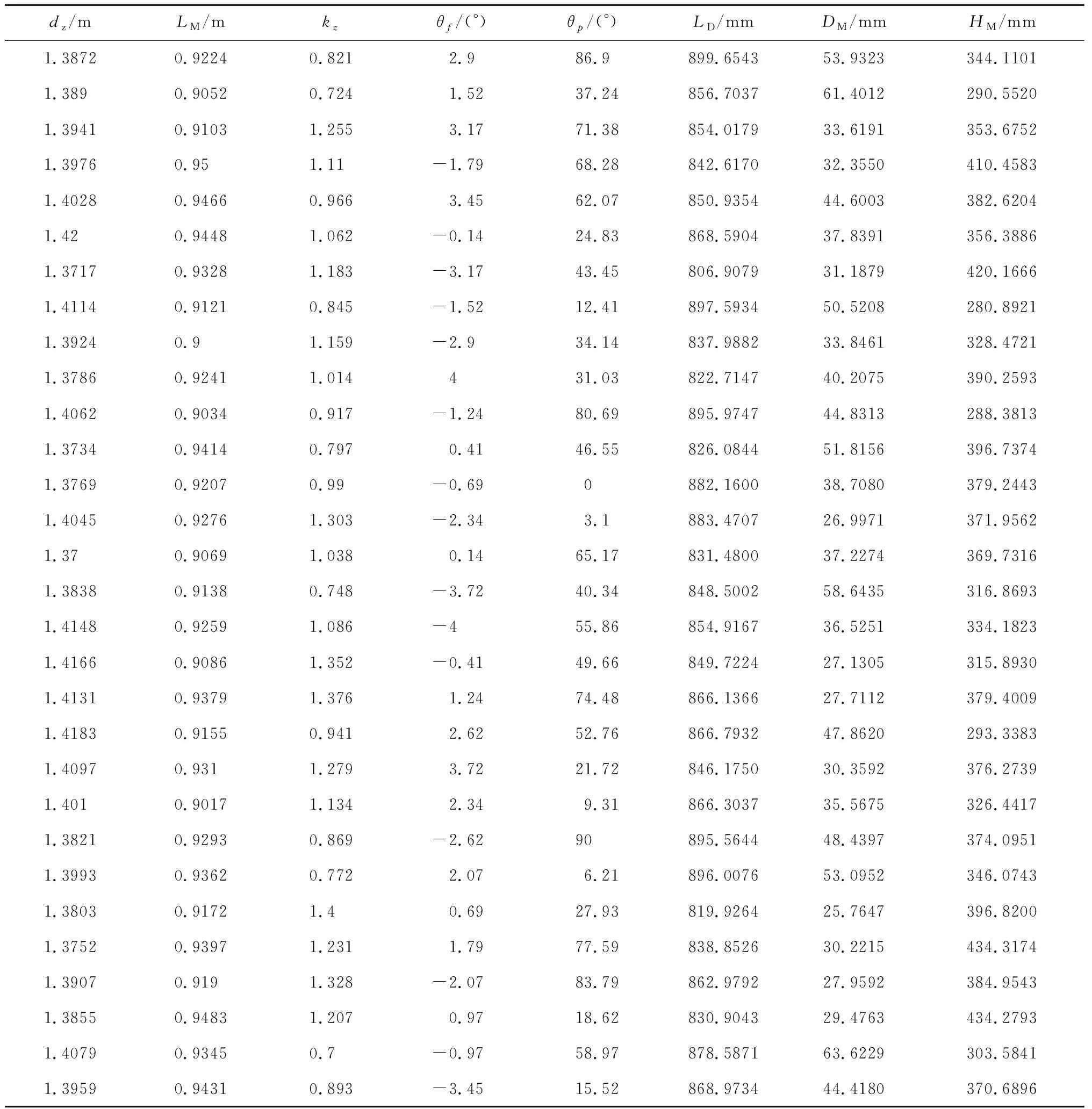
表4 实验设计结果Table 4 Result of design of experiment

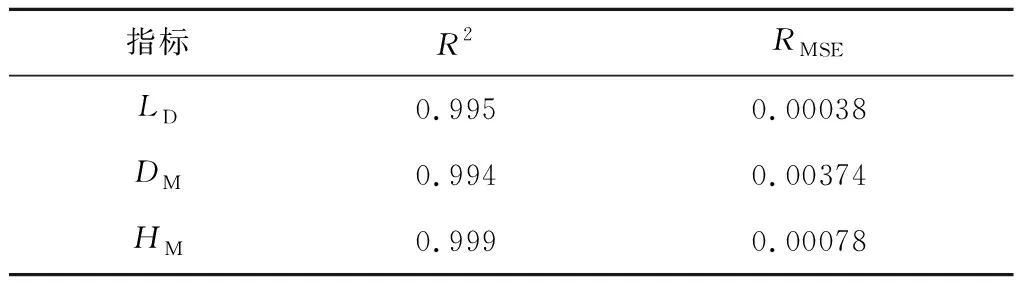
表5 响应面精度检验结果Table 5 Accuracy analysis table of response surface models

max{LD-ave,HM-ave} s.t.DM-max≤75HM-min≥360x(L)O≤xO≤x(U)O(12)

本文结合式(9)与式(11)，利用多元积分法求解LD-ave与HM-ave，鉴于θf与θp相互独立，多元积分求解如下所示：

(13)

122.948LM-121.739dzkz+1148.830dzLM

(14)

HM-ave=-21936.723+23353.525dz+13572.952LM-

402.763dzkz-183.107kzLM

(15)

本文结合式(10)与式(11)，在给定dz，LM，kz取值下，利用MIGA算法求解以θf,θp为设计变量的DM-max与HM-min，算法参数配置如表6所示。

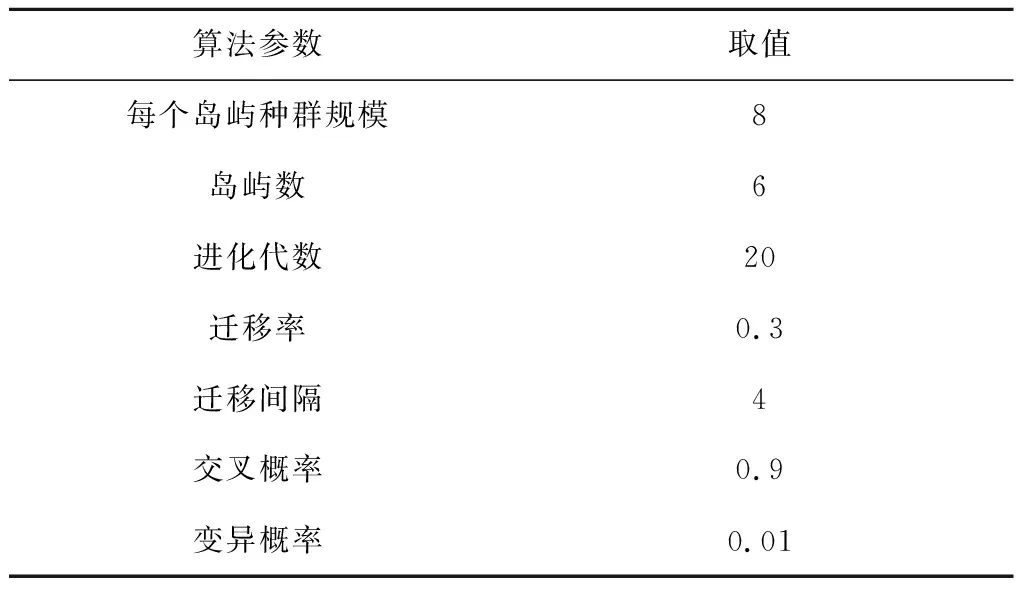
表6 MIGA算法参数配置Table 6 Parameters configuration of MIGA

对于整个多目标优化数学模型，本文利用NSGA-II算法求解，算法参数配置如表7所示。

表7 NSGA-II算法参数配置Table 7 Parameters configuration of NSGA-II

综上，得到不确定着陆姿态下的着陆器缓冲机构分级优化设计流程如图10所示。

经过优化迭代计算，得到帕累托最优解集，并绘制帕累托前沿曲线如图11所示。

由于着陆器的翻倒更能直接导致探测任务的失败，故在帕累托最优解集中选取着陆器抗翻倒能力最强的解作为本文的最优解，dz，LM和kz的取值如表8所示。

表8 最优解取值Table 8 Value of optimum solution

将最优解代入ADAMS模型，再次抽取2000个样本点进行Monte Carlo模拟，根据2000组仿真结果绘制性能指标值的散点图如图12所示，并得到表9所示的软着陆性能分析结果。

将表2、表9的分析结果做对比可知：相比于优化前，优化后着陆器的HM超出许用值的工况数由73组减为0组，LD与HM的平均值分别提升了3.546%和5.140%，优化效果明显。

4 结 论

本文在某型着陆器软着陆动力学仿真模型的基础上，结合Monte Carlo法研究了着陆姿态不确定条件下的着陆器软着陆性能，并结合优化拉丁超立方实验设计得到样本点，建立了以着陆器缓冲机构构型参数和着陆姿态参数为输入、软着陆性能指标值为输出的响应面模型；针对着陆姿态不确定条件下的着陆器缓冲机构优化问题，基于响应面模型，提出了结合NSGA-II算法与MIGA算法的分级优化求解方法，并计算得到了使着陆器软着陆性能最佳的缓冲机构构型参数；再次结合Monte Carlo法与动力学仿真模型校验优化结果，优化后着陆器的抗翻倒能力和底面抗损坏能力分别提升了3.546%和5.140%，且尾喷管底面中心点距星球表面的最小距离与辅助支柱最大缓冲行程均不超出许用值。

指标超出许用值工况数平均值LD/mm0868.558DM/mm037.605HM/mm0374.169

本文所述的研究方法具有成本低、效率高等特点，也可为其他型号腿式着陆器的优化设计提供参考。