空间自旋目标平动补偿与微动特征提取方法

顾福飞，傅敏辉，凌晓冬，张 印

(中国卫星海上测控部，江阴 214430)

0 引 言

自旋运动是航天器、碎片等空间目标常见的运动形式，自旋运动所产生的微多普勒(micro-Doppler, m-D)特征为空间目标的分类、识别提供了重要信息。随着各国对空间资源利用的日渐重视，近年来国内外学者针对空间目标的m-D特征分析与提取问题进行了大量研究[1-4]。从公开发表的文献来看，空间自旋目标的平动在精确补偿条件下，其m-D特征通常表现为正弦曲线。现有的经验模式分解算法[1]、扩展Hough变换[5]以及正弦调频Fourier-Bessel变换[6]等方法能够对其进行准确提取。然而空间目标通常情况下具有高速的径向运动，精确的平动补偿是难以实现的，必然存在估计误差，这将导致目标的m-D特征曲线附加了剩余平动引起的调制项，与理论的m-D特征曲线存在差异，给常规的特征提取带来困难。

文献[7]提出先利用经验模式分解方法进行平动补偿，然后再利用Hough变换进行特征提取。该方法需要基于目标的强散射中心信息，并且所需的计算量较大。文献[8]提出了多级延迟共轭相乘和Hough变换的平动补偿与特征提取方法。当目标包含多个散射点时，需要依次提取每个散射点的微动特征，因此该方法效率较低。文献[9-10]研究了速度和加速度对微多普勒的影响，提出了基于频谱重排和模板的平动补偿方法，但是该方法对噪声较为敏感。文献[11]基于目标整体运动信息，利用Radon变换对平动参数进行估计，需要较长的积累时间。文献[12]研究了弹道进动目标平动补偿方法，该方法只能够针对具有轴对称特性的目标进行处理。

本文针对空间目标平动补偿不够精确，存在一定误差情况下的m-D特征提取问题进行研究，提出了一种基于延时共轭相乘和微动分解的自旋目标平动补偿与特征提取方法。首先分析了空间自旋目标的回波信号模型，其次利用延迟共轭相乘处理，估计目标的加速度信息，然后基于目标的微动特征构建了冗余的微动原子集，并对加速度补偿之后信号进行微动分解补偿处理，进一步搜索补偿结果的最大谱峰，其所对应的微动补偿原子即为自旋目标的微动分量，利用最大谱峰的频率值计算目标的剩余初始速度。

政策二：4月18日，农业农村部、中央机构编制委员会办公室、国家发展和改革委员会、财政部、人力资源和社会保障部、自然资源部、黑龙江省政府、广东省政府共同制定了《中央直属垦区“部省双重领导、以省为主”管理暂行办法》。

1 回波信号模型

雷达与空间目标的几何位置关系如图1所示，为了便于描述空间目标相对于雷达的空间三维自旋运动，建立雷达坐标系UVW和目标本地坐标系XYZ，同一向量在目标本地坐标系和参考坐标系中具有不同的表达式，它们之间的关系由欧拉(Euler)旋转矩阵确定。

式中：tm为慢时间，f0为载频，σp为第p个散射点的反射系数，rp(tm)为第p个散射点在任一慢时间tm与雷达的瞬时斜距。在远场条件下，基于平面波近似，瞬时斜距rp(tm)可写为：

(1)

设定雷达发射信号为p(t)=exp(j2πf0t)，观测时间为Tc，则目标第p个散射点的回波信号为

江苏省泰州引江河管理处高港枢纽位于长江下游北岸泰州市高港区口岸镇西北约3km处，枢纽节制闸和泵站采用闸站结合布置形式。高港枢纽节制闸共5孔，每孔净宽10 m，设计流量为440 m3/s，采用弧形钢闸门；泵站采用堤身式双向箱形流道结构,立轴双层进出水流道，配开敞式轴流泵9台，每台机组设置4扇平面钢闸门，可通过下层流道实现160 m3/s的自流引江。高港枢纽1999年建成时，节制闸和泵站的监控系统采用SUPCON JX-300型DCS集散控制系统，如图1监控系统部分所示，在中央控制室可实现对闸门的操作控制，并可采集闸门开高及上下游水位，实时显示。

(2)

为了便于矩阵相乘处理，将信号s′(tm)进行对角化，得到S=diag(s′(tm))。那么回波信号的微多普勒补偿处理可表示为

(3)

设定目标中共有P个散射点，由于目标到雷达初始距离对回波信号的多普勒没有影响，因此暂不考虑式(2)中的r0，那么可以得到空间目标的回波信号表达式为：

(4)

可见信号s(tm)由两部分组成：第一部分由目标的平动决定，可近似为关于慢时间tm的多项式相位信号；第二部分由目标的微动形式决定，可近似为多分量正弦相位信号。进一步，对信号s(tm)做时频分析即可获得空间目标微动特征的时频域表示。但是由于平动项的存在使得时频面的微多普勒效应不再是标准正弦信号形式，这使得微多普勒特征理解和提取存在困难，需要寻找平动补偿方法。

2 延迟共轭相乘处理

设定τ为固定延时，那么根据式(4)，一阶延时共轭相乘处理可写为

P1[s(tm),τ]=s(tm)s*(tm-τ)=

…,dT(A2,θK),…,dT(AI,θK)]M×IK

Aqsin(2πfq(tm-τ)+θq)]}

(5)

令

[Apsin(2πfptm+θp)-

Aqsin(2πfq(tm-τ)+θq)]}

(6)

对补偿处理之后的信号S′做关于慢时间tm的傅里叶变换处理，记Ω为傅里叶变换矩阵，那么该处理用公式可表示为

sin(2πfctm+θp-Ψ)))

(7)

培养学生的预习兴趣是途径，指导预习方法是关键。要想让学生掌握自学的本领，我们就要注意方法的指导。预习的方法多种多样，根据小学高年级学生的年龄、认知规律等特点，老师们可以引导学生掌握以下预习方法：

(8)

需要说明的是，由于目标的速度和加速度的估计主要是通过信号多普勒谱的中心频点计算得到的，为了避免产生多普勒模糊，中心频点不能超过fPRF/2,其中fPIF表示脉冲重复频率。因此，进一步根据式(10)和式(17)，本文方法可估计的目标速度和加速度的范围为

(9)

(10)

(11)

从式(11)可以看出，加速度补偿之后的信号s′(tm)的相位项包括两部分，第一部分是关于慢时间tm的线性项，与目标的速度v相关；第二部分是目标的微多普勒项。如果没有微多普勒项，直接对信号s′(tm)做傅里叶变换即可获得目标的平动速度。但是由于微多普勒项的存在使得信号s′(tm)的多普勒谱存在展宽等现象，无法直接获得目标的平动速度。下面提出一种微动补偿方法，构造冗余的微动原子，与加速度补偿之后的信号s′(tm)相乘处理，然后搜索最大谱峰获得准确的微动原子集，并利用其位置信息获取目标的平动速度，进而实现对回波信号的运动补偿与微动参数的提取。

3 参数估计

从式(11)可以看出，当自旋目标的旋转周期fc已知，目标的微多普勒特征参数主要由参数(Ap,θp)确定，因此，将Ap和θp在设定的取值范围内，均匀划分为I×K个离散的值，也就是Ap∈{A1,…,Ai,…,AI}和θp∈{θ1,…,θk,…,θK}。那么微动原子信号可表示为

(12)

毕竟是铁家伙，推土机在村长指挥下，横推竖扒拉，三下五除没，就将那些砌好的墙头以及堆着的砖头瓦块橼皮檩条推下了岭，在山头上清理出一块足球场大的地坪来。

Ψ= [dT(A1,θ1),…,dT(A1,θK),…,dT(A2,θ1),

[Apsin(2πfptm+θp)-

(13)

式中：r0为斜距常量，v是目标运行速度，a为加速度，Ap为观测平面内的有效转动半径，fc为旋转频率，θp为初始相位。ftr为目标平动引起的相对转速，通常目标自旋转引起的角度变化远大于相对转动角度，因此ftr可忽略不计[13]。那么第p个散射点的慢时间回波信号表达式为：

(14)

当p≠q时，PM为微动散射点的交叉项，没有实际意义。当p=q时，PM为微动散射点的自相关项，因此式(5)可进一步写为

(15)

可以看出，F有IK个微动补偿结果。考虑到准确的微动补偿是没有多普勒展宽，其所对应的谱峰是最大的。因此可用式(16)表示

s.t.F=Ω·S·Ψ(Ai,θk)

(16)

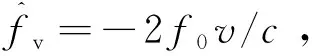
(17)

根据上述分析，可得空间目标平动补偿与特征提取方法的步骤如下：

1)获得空间目标的旋转频率fc，根据式(5)对信号以τ=1/fc的整数倍为延迟进行共轭相乘处理，得到P1[s(tm),τ]；

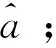
3)对回波信号s(tm)进行加速度运动补偿处理，得到s′(tm)；

4)构建冗余的微动原子集；

5)对补偿结果做傅里叶变换处理并搜索最大谱峰，估计出目标的运动速度以及最优的微多普勒补偿基。

语篇中的最后一封书信是萧涧秋写给陶慕侃的。送信人是“邮差”,是真正意义上比较正式的“挂号信”,发信人署名是“女佛山后寺萧涧秋缄”。这封信影响巨大、反应强烈,涉及多方主体。例如：

由于质心是物质系统上被认为质量集中于此的一个假想点，表示质量分布的平均位置，故可以据此来确定撒料点在撒料区域中的平均位置，以确保最终撒料能够覆盖到实际需要撒料区域.设撒料区域像素点集合 Ui中的元素是 p（x，y），n 为集合 Ui内像素点总数量，质心坐标 Z（x，y）的求解公式为式（9）.

(18)

(19)

4 仿真校验

本部分进行仿真试验用以校验所提方法的有效性。设定空间目标包括3个散射点，分别记为P1，P2和P3，反射系数均设置为1，有效旋转幅度分别为0.2 m，0.4 m以及0.5 m，初始相位分别为30°，45°和60°。目标径向平动剩余速度v=15 m/s，径向加速度a=5 m/s2。雷达中心频率为10 GHz，fPRF=4000 Hz，回波信号时长1 s。雷达与空间目标的位置关系如图1所示。

将表面活性剂和助表面活性剂按质量比(Km)混匀，得到混合表面活性剂(Smix)；将油相(Oil)和Smix混匀，得到混合油相；在混合油相中缓慢滴加水相，不断搅拌，直至形成透明的体系，记下体系发生透明或浑浊变化时的各组分用量，用origin8.5绘制伪三元相图。根据纳米乳区大小，筛选合适的纳米乳体系。

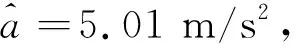
下面对加速运动补偿处理之后的信号进行微动补偿处理。回波数据在{Ap,θp}域的微动补偿分解结果如图3所示，颜色较深的三个点的横纵坐标表示目标散射点的初相和幅度参数。参数值分别为(0.2 m,29°)，(0.4 m,44°)和(0.5 m,59°)。与实际值基本一致。进一步对微动补偿完信号搜索最大谱峰，三个最大谱峰点所对应的信号频谱如图4所示。利用最大谱峰的位置信息和式(17)可计算得到目标的初始剩余平动速度为15 m/s，与真实值一致，说明了所提方法估计目标速度的准确性。至此完成了空间运动目标平动参数估计以及微动特征的提取处理。

科研费用控制不当，虚列支出，违反国家相关规定，导致科研费用支出失控，造成经济损失。例如，超预算使用，超范围发劳务费等等。

本文算法能够完成目标平动补偿处理的前提是获得目标的自旋频率。鉴于此，下面讨论分析在不同的旋转频率估计误差情况下对目标加速度估计值的影响。设置旋转频率的误差范围为-0.1～ 0.1，图5给出了不同旋转频率估计误差情况下获得的加速度估计结果。从图5可以看出，旋转频率误差范围控制在-0.05～ 0.05，加速度估计值能够控制在4～ 6 m/s2之间，与真实值相接近，可实现对回波信号的加速度补偿处理。

一直觉得大学就是社会的预备役，一场磨炼我们身体和心智的旅程。在这个五光十色的花花世界里，在这个混杂着青春热血和荷尔蒙的世界里，在这个第一次正式离开父母羽翼呵护独自飞翔的世界里，有精彩，有诱惑，有钩心斗角，有励志，有颓废……四年之后，有人迅速成长，有人华丽蜕变，有人颓废报废。

表2中给出了经多风电场无功优化后各风电场在不同场景下的无功出力及并网点高抗投入组数(无功出力负号表示吸收无功,正号表示发出无功)。

进一步对比本文微动特征提取算法与Hough变换[5]以及复OMP算法[14]的性能。主要对比微动参数提取的准确性以及MATLAB运行所占用的时间。三种算法均能够准确提取目标的微动幅值，且精度相当，但是相位估计方面，本文算法和复OMP算法要略优于Hough变换算法。在算法耗时方面，复OMP算法耗时最长，本文算法与Hough变换算法相当，这是因为本文算法主要通过矩阵相乘和快速傅里叶变换实现，因此复杂度较低，耗时也较短。

钢渣作为混凝土骨料利用可以提高混凝土强度和耐久性，用钢渣配制C30混凝土，结果表明混凝土的抗压和抗折强度均明显提高[33]，也有研究表明标准养护下钢渣对混凝土抗压强度影响小，而高温养护下可提高混凝土抗压强度[34]。对碎石混凝土和全钢渣集料混凝土的抗氯离子渗透性能研究表明全钢渣混凝土具有更好的耐久性，但钢渣粗骨料混凝土的体积稳定性不良是一个显著的劣势。

5 结 论

针对空间自旋目标，提出了一种基于延时共轭相乘和微动分解的平动补偿与特征提取方法。此方法充分利用回波信号特征，利用延时共轭相乘消除微动影响估计目标的加速信息，然后在冗余原子集上进行微动分解补偿，利用最大谱峰获取目标的微动特征与速度信息。仿真试验表明，所提方法可准确估计自旋目标的平动参数和微动特征信息。需要说明的是，本文算法中微动参数离散化间隔的选取需要综合权衡估计精度与重构准确性，并且受多普勒模糊的影响，本文算法只能够估计径向运动补偿之后存在的剩余平动参数，如何拓展本文方法进行目标完整的平动参数估计需要进一步研究。

接尘缸和盖需用10%HCl浸泡24h后洗干净再使用，否则会带来缸体的污染；采样缸的放置高度需距离地面10m以上，否则会带来由地面尘土的影响；当地燃放烟花爆竹时间需把缸盖盖好，结束后及时把缸盖去掉继续接降尘。