靶向谱修正迭代法

吴光明,鲁铁定,2,3,邓小渊,4,吴建江,5

(1.东华理工大学 测绘工程学院,江西 南昌 330013;2.流域生态与地理环境监测国家测绘地理信息局重点实验室,江西 南昌 330013;3.江西省数字国土重点实验室,江西 南昌 330013;4.浙江省地理信息中心，浙江 杭州 310000;5.浙江省地球物理技术应用研究所,浙江 杭州 310014)

病态问题在测量数据处理过程例如在控制网平差[1]、GPS快速定位[2-3]、航空重力向下延拓[4-6]等领域时常碰见。处理病态问题常见方法有Tikhonov正则化法[7-8]、岭估计[9-10]等，然而岭估计和正则化法改变了方程的等量关系，使得估计结果有偏并且岭参数和正则化参数确定困难[11-12]。

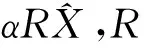
1 谱修正迭代法

对于经典平差模型

L+Δ=AX.

(1)

式中：L为n×1观测值向量，A为m×n系数矩阵，X为n×1待定参数，Δ为观测向量的噪声，Δ～N(0,σ02I)。其最小二乘估计及估计的协方差为

(2)

(3)

当法矩阵AΤA出现病态(条件数一般大于103)，则法矩阵求逆将会表现得不稳定，导致求解出的参数估值不可靠[12]。

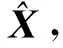
(4)

或者

(5)

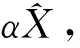
(6)

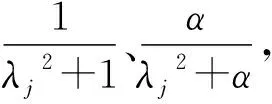
2 靶向谱修正迭代法

谱修正迭代中的(ATA+αI)-1与岭估计相似，岭估计式为

(7)

(8)

整理后

(9)

式中：R是靶向矩阵，其构造方法是基于较小特征值对应的特征向量而构成，

(10)

式中：R1是正则化矩阵，Gi是法矩阵ATA的特征向量。小特征值的判定方法可用特征值标准差分量之和占标准差比重达到95%以上[19]，即

(11)

式中：Λi是法矩阵ATA的特征值。将R1作为靶向矩阵并代入式(8)则整理得到本文靶向谱修正迭代式

(12)

谱修正迭代结果是无偏估计，根据文献[13]证明方法，本文靶向修正迭代结果也是无偏的。只要迭代矩阵α(ATA+αR)-1·R的谱半径小于1，迭代就能收敛[20]。在对α(ATA+αR)-1·R进行谱分解，得到

α(ATA+αR)-1·R=

(13)

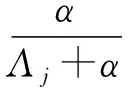
谱修正参数α选择有多种方法[16-18],没有统一结论。因此本文根据文献[18]的方法，选择一个较长区间、一定步长的参数，讨论不同参数条件下，两种方法迭代结果的比较。

3 算例及分析

3.1 算例1

采用文献[4]中的模拟病态问题算例，法矩阵条件数是4.1847×105,严重病态，其中未知参数的真值为X=[111111111]T。为比较两种方法的估计结果，取迭代初值为X=[0.80.80.80.80.80.80.80.80.8]T或其他初值均可，不能选择最小二乘估值作为迭代初值，若选择最小二乘估值将无法迭代。根据文献[18]的方法，取谱修正参数α=1，10，20，30，分别用最小二乘估计、谱修正迭代法、靶向谱修正迭代法对这个问题进行解算，结果见表1。

表1 两种算法的解算结果

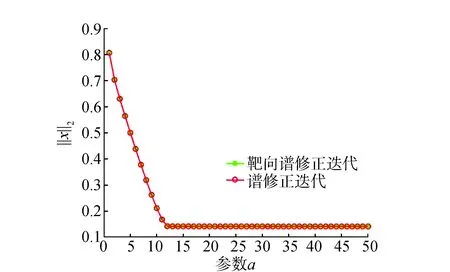
图1 两种方法结果

从图1可以看出，两种方法的差值范数基本相等，结果基本一致；见图2(a)图是α=1～50，由于竖轴刻度较大，两种方法迭代次数也近乎相等；由图2(b)看出，在α>11时，本文方法迭代次数少于谱修正迭代法。根据这个算例，靶向谱修正迭代法与谱修正迭代法相比，在参数估计和差值范数上没有较大变化；但在参数逐渐增大时，迭代次数降低，计算效率提高，体现出本文方法的优势。

图2 两种方法迭代次数

3.2 算例2

表2 两种算法的解算结果

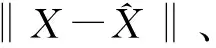
从图3可以看出，图3(a)是α=1～17，两种方法的差值范数基本相等；由图3(b)看出，在α>17时，本文方法差值范数小于谱修正迭代法。见图4，1<α<17时，两种方法迭代次数基本相等；而α>17时，本文方法迭代次数远小于谱修正迭代法。这个算例表明，参数逐渐增大，两种方法在参数估计、差值范数、迭代次数上先是没有较大变化，但参数继续增大时，本文方法解算的差值范数和迭代次数均降低，进一步验证靶向谱修正迭代法高效、快速解算。

图3 两种方法解算结果

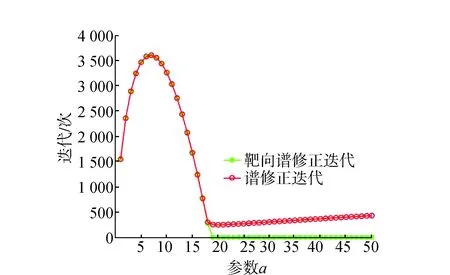
图4 两种方法迭代次数

4 结束语

谱修正迭代法是修正法矩阵所有谱且结果是无偏估计，而一般病态问题是法矩阵的几个谱奇异，因此存在谱多余修正问题。针对该问题，本文提出靶向谱修正迭代法，即将谱修正迭代矩阵中的单位阵变换成靶向矩阵，迭代过程中只修正法矩阵奇异的谱。通过模拟算例对比两种方法解算的估计结果、偏差范数和迭代次数，得到以下结论：

1)谱修正参数相同条件下，两种方法迭代矩阵的谱半径相等，且估计结果均是无偏的；

2)伴随着参数增大，本文方法的解算的参数估值将优于谱修正迭代，并且偏差范数更低、迭代次数相比也更少。

因此，在探讨处理病态问题时，相比谱修正迭代法，本文方法在估计结果更优且快速迭代，计算效率高。本文递增选取参数，参数选择未深入分析，因而参数如何选取有待进一步研究。