线性参照系与大地坐标系的相互转换

邓兴升， 黄小鹏

(长沙理工大学 交通学院, 长沙 410114)

在道路交通领域，位置信息不是由单一的坐标确定，而是根据实际需求配合线性参照系统(Linear Referencing System, LRS)共同确定[1]。由于道路的线性特征，采用线性参照系统更有优势，符合人们对道路要素描述的习惯和理解能力。用大地坐标来描述道路特征点的位置，往往没有用里程数更直接、更易理解；线性参照系统也是为了解决交通网络中事件定位和表达而设计的。目前高速公路普遍采用里程桩进行线性定位[2]，以距离替代坐标来定位空间事物或事件。交通运输地理信息系统GIS-T(Geographic Information System for Transportation)的定位采用线性参照系统[3]，是与常规GIS的区别之一；面向对象的公路网络及立交模型均是基于线性参照系统[4]。单纯二维坐标参考系统并不适合大型公路地理信息系统建设[5]，现有GIS-T模型一般同时采用两种空间位置参照系，即一维线性参照系和二维空间参照系[6]。线性参照系的显著特点是可以采用线性分段技术在GIS中完成空间相对位移定位[7]。

卫星定位技术常用于获取道路特征点的三维大地坐标，但表达交通信息时常用线性参照方法LRM(Linear Reference Method)和线性参照系，而不采用空间参照方法。线性参照方法是在一个定义好的交通网络中由已知位置和路径，在LRS空间通过与已知参照点间的偏移距离，来确定未知位置的度量方法。基于一维线性系建立空间数据模型，能够将一维线性坐标转换为实际地理空间坐标[8]。根据需要可将路段进行动态分段，并将属性沿程变化存储为独立事件属性表，使一维线性参照系为基础建立的各类属性集能与二维参照系为基础建立的空间位置相关联[9]。实现线性参照系与大地坐标系之间的融合和高效转换是一项重要的基础工作，本文采用模型直接计算两坐标系的转换参数，给出道路弯曲度近似度量的两个指标，及两坐标系之间相互转换的方法，其中大地坐标对球面经纬度和空间直角坐标两种形式均适用，并列举实例进行分析验证。

1 线性参照系与大地坐标系相互转换

1.1 线性参照系统的建立

线性参照系统最早由Baker和Blessing在1974年提出，通常由交通网络、线性参照方法和参照基准控制3部分组成。实际道路网形状复杂，基线网仅是一个抽象的近似映射，提供不同线性参照方法间的定位参照及相互转换基准[10]。基线网中特征点线集合，由锚固点(Anchor Points)及锚固段(Anchor Sections)组成。锚固点即道路特征点，具有明显地物特征、且位置不易改变，如道路起终点、主要道路交叉口、大中型桥梁中点、特征里程桩点等。锚固段即路段，由两个有序的锚固点组成。锚固点的定位包括平面坐标及线性参照距离，参照点即某锚固段的里程零点，是线性参照系的原点。参照点可采用具有重要地理位置的锚固点，由于线性参照系统采用动态分段机制，在一个基线网中，任何一个锚固点根据需要都可能作为参照点。

1.2 道路弯曲度计算与线性插值

由于线性插值是将锚固段近似视为直线处理的，因此需对道路弯曲度进行度量。道路弯曲度评价可以采用两个指标：最大弯曲度和曲直比。最大弯曲度是指一条路线内各迹点至锚固段的最大偏离度，由最大弯曲矢量与路线长度之比的百分比来度量。曲直比是指锚固段的曲线里程数与首尾两点直线距离的比值。这两个指标越大，道路弯曲度越大，对线性插值计算越不利。曲直比为1时，表示道路线形为直线，这时采用线性插值转换计算可视为无误差。

线性插值法原理简单但精度较低，只可满足基本交通应用需求[11]。两点在参考椭球面的近似直线距离为:

(1)

其中d为两点间近似距离(单位为m)；c为1秒地心角对应的椭球面弧长，其近似值为30 m；(b1,l1)、(b2,l2)分别为点1和点2的纬度与经度，坐标单位需由(° ′ ″)转换为(″)。插值点i到锚固段起始点的里程Ki为:

(2)

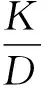
(3)

其中(b1,l1)为锚固段起始点坐标；(b2,l2)锚固段终点坐标，K为锚固段的里程数。式(1)—式(3)是基于锚固段近似为直线推导的，仅适用于直线路段。

1.3 空间曲线拟合

实际上，大部分路段是远距离大半径的曲线路段，线性近似会带来很大的转换误差。基于道路曲线要素的动态分段模型算法[12]计算精度较高，但道路线型参数缺失时，在实现过程中会面临很多困难[13]，且计算复杂不利于高效快速转换。采用道路设计的曲线元素如缓和曲线、圆曲线来表示曲线路段较合理，但在现实中特别是旧路改造时，通常会面临曲线元素与方位参数缺失等问题。因此需采用其它参数方程对曲线路段进行拟合，建立线性参照系统里程数与大地坐标的函数关系，空间曲线用以下参数方程来描述：

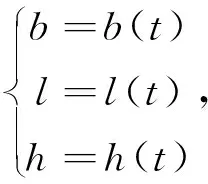
(4)

其中(b,l,h)分别为空间点的纬度、经度、大地高；(x,y,h)分别为空间点的高斯平面坐标与正常高，t为里程数变量。分段3次样条函数可用来拟合道路平面线形[14-16]，(b,l,h)或(x,y,h)可采用分段3次样条函数来拟合：

f(t)=c3(t-t1)3+c2(t-t1)2+c1(t-t1)+c0.

(5)

其中c0,c1,c2,c3为待求的模型系数；t1为区间[t1,t2]的起始点。

根据实测点进行分段，每段都有各自的模型系数。3次样条函数在每个子区间上建立一个3次多项式，在分隔点处的插值等于观测值，在分隔点处具有连续的一、二阶导数，且满足自然边界条件；在节点处具有连续性，插值曲线为光滑分段多项式[17]。

由于里程数是单调递增的，不会多值重复，因此区间分段是可行的，由里程数转换到大地坐标不存在多值性。反之，由大地坐标转换到线性参照系时，由于道路线形可能出现回旋，如立交桥在立体交叉时具有相同平面坐标的点，是空间上不同的点[4]。路面中心线轨迹的大地坐标不满足单调性条件时，需要根据具有单调性的另一维坐标，例如高程h，建立与里程数t的函数关系，实现逆向转换，或进行必要的分段处理。

t=f(j)|j∈ b, l, x, y, h, r.

(6)

其中f(j)与式(5)形式上相同，j是b,l,x,y,h,r(r为坐标点到区段起始点的向径)中的任何一个具有单调性的坐标或向径，要求该数值在整个区段单调增或单调减，不得有重复值，从而建立与里程数的一一对应关系。

1.4 计算流程

1.4.1 大地坐标系转换到线性参照系

1)建模数据点坐标与里程实测，大地经纬度坐标由(°)(′)(″)转换为以(″)为单位；

2)取大地坐标中具有单调增或单调减特性的某一维坐标或向径，由分段3次样条函数式(5)～式(6)建立与里程数的对应关系，求得模型系数；

3)根据待转换点的大地坐标和转换模型系数，将其转换到线性参照系里程数。

1.4.2 线性参照系转换到大地坐标系

1)建模数据点坐标与里程实测，大地经纬度坐标由(°)(′)(″)转换为以(″)为单位；

2)里程数是单调增的，采用式(4)—式(5)分别建立里程数与3维大地坐标的分段3次样条函数模型，每一维坐标建立一个模型，计算模型系数；

3)根据转换·模型系数将里程数转换为大地坐标。

2 算例分析

2.1 实验数据

本实例选择某一实际曲线路段作为实验对象，其曲直比为1.145，最大弯曲矢量为72.3 m，最大弯曲度为21%。建立转换模型时根据道路等级和转换精度要求，曲线路段数据点间隔应尽量小，通常以20 m为宜[15]。从实测数字地形图中解析得到大地坐标及里程数据如表1所示，其中x,y坐标采用地方独立坐标系，解析坐标精度为±10 cm，里程数精度为±30 cm。

表1 大地坐标及里程表 m

2.2 大地坐标系转换到线性参照系

将实验点A,B,C的大地坐标转换为以里程桩为0的线性参照系里程数，由于在该区间中x坐标不单调而y坐标单调增加，因此采用空间曲线拟合法由y坐标建立与里程数的函数关系。根据计算流程1.4.1由坐标y转换到里程t的模型系数如表2所示。

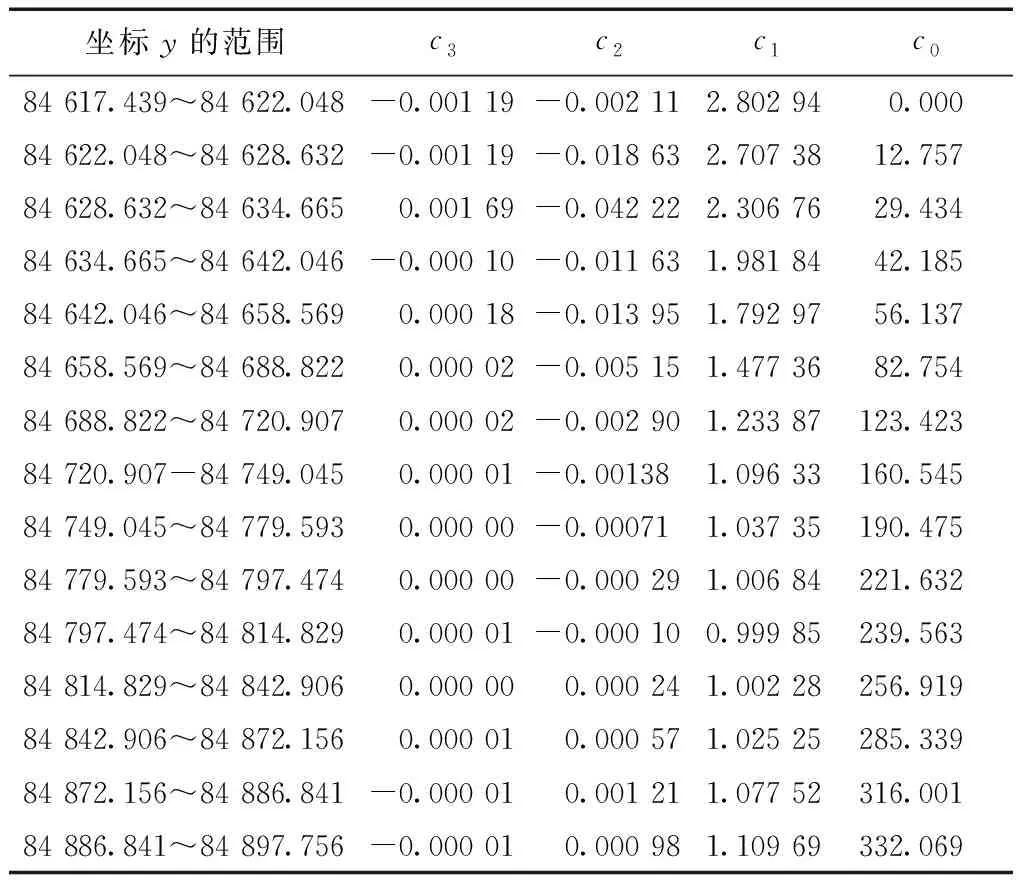
表2 分段3次样条函数t=f(y)模型系数

根据模型系数得到转换计算结果如表3所示，其中转换里程与实测里程差值最大为0.543 m。

表3 大地坐标转换到线性参照系计算结果 m

2.3 线性参照系转换到大地坐标系

将实验点A,B,C的线性参照系实测里程数转换为大地坐标，根据计算流程1.4.2，由里程t转换x坐标的模型系数如表4所示。

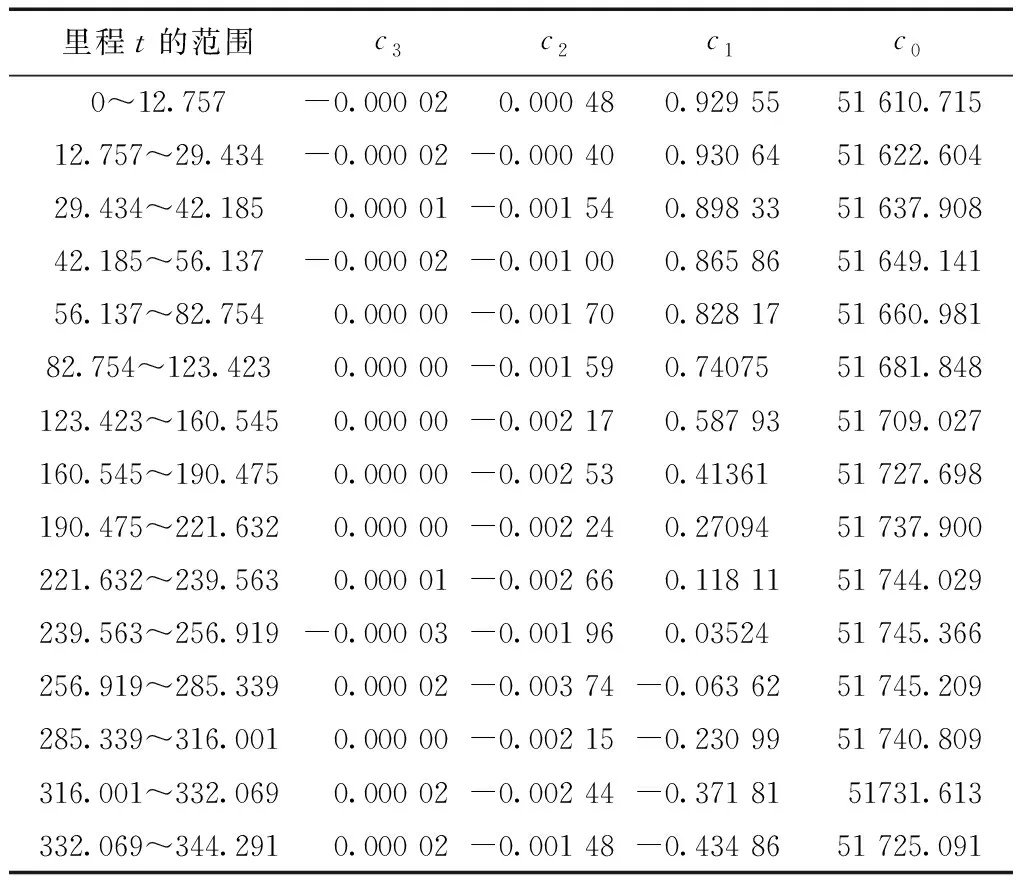
表4 分段3次样条函数x=x(t)模型系数

由里程t转换y坐标的模型系数如表5所示。

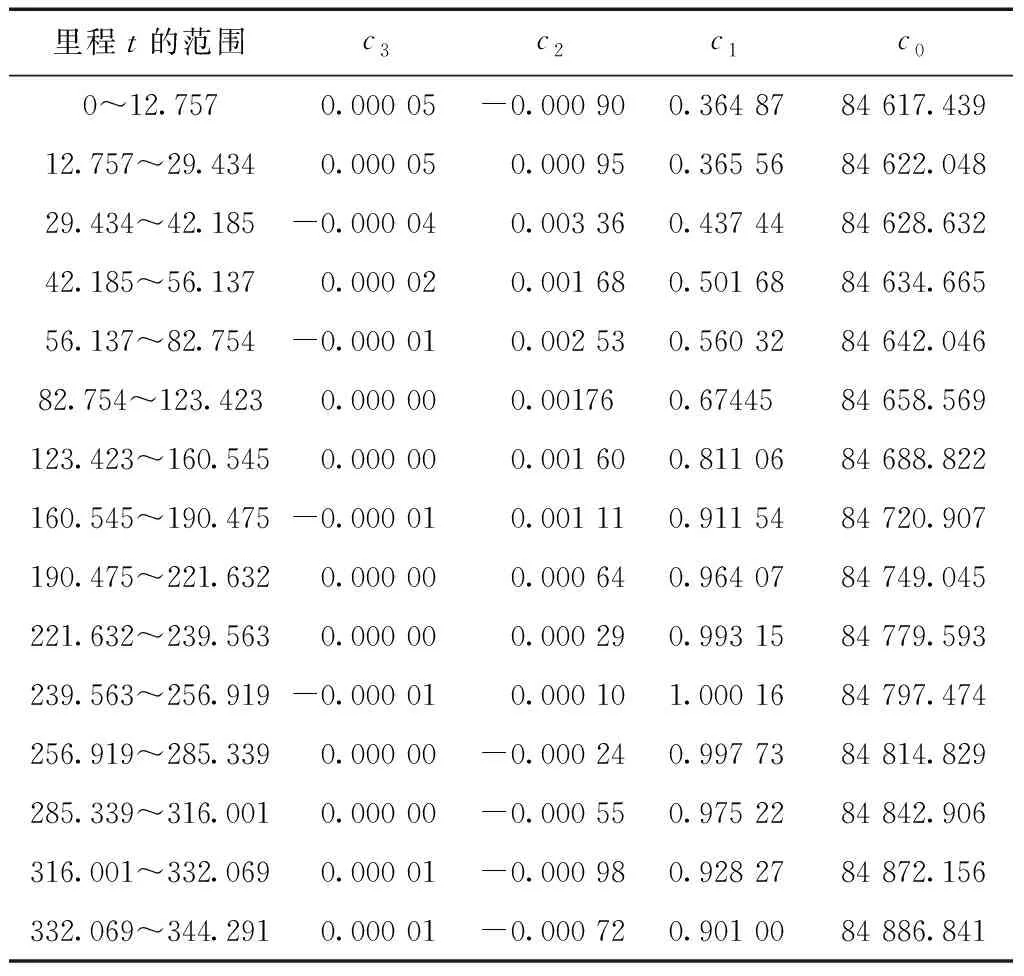
表5 分段3次样条函数y=y(t)模型系数

由表4、表5可知，3次项系数c3接近为0，表明该曲线段采用二次样条曲线拟合即可。由模型系数计算得到大地坐标转换结果如表6所示，其中坐标转换误差最大为0.402 m。

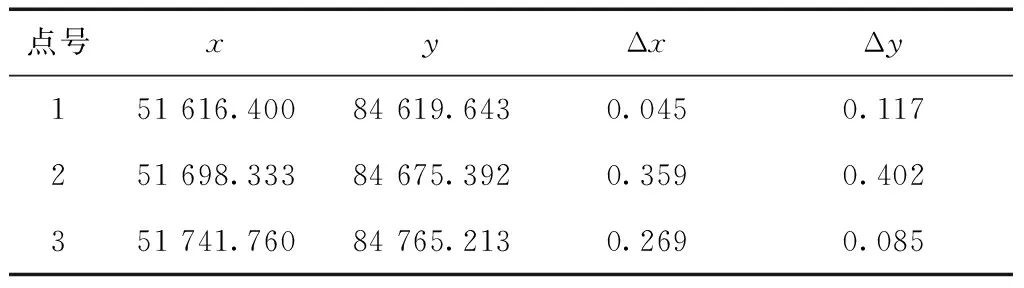
表6 线性参照系转换到大地坐标系计算结果 m

直线路段转换试验分析结果表明，在直线路段3次样条函数c3,c2的值近似为0，与直线方程等价，因此分段3次样条函数同样适用于直线路段的转换。采用分段3次样条函数，针对复杂道路线形不要求函数有较强的拟合能力，拟合曲线也不会在数据点间产生多余的摆动，转换结果满足交通应用需求。

3 结 论

线性参照系与大地坐标系的相互融合与高效转换，是智能交通信息系统的一项基础工作，适用于解决道路特征点的空间定位问题。本文在两坐标系之间建立函数关系进行直接相互转换，给出度量道路弯曲度的两个指标，及两坐标系相互转换的两类方法，即线性插值法和分段3次样条曲线函数模型法。分段3次样条函数法对直线和曲线路段都适用，要求建模数据点具有一定的密度且能反映道路线形特征，数据点密度较高且实测精度高时模型误差可忽略。本文实验结果显示，线性参照系统与大地坐标系的相互转换误差可达±0.5 m，主要误差来源于坐标和里程数据的测量误差。