有偏改正的正则化抗差方法

范 伟，潘国荣

(同济大学 测绘与地理信息学院，上海 200092)

在摄影测量附加参数的自检校平差中，为了补偿系统误差，引入大量的附加参数地抵偿系统误差的影响。过度的引入附加参数，会导致附加参数之间或附加参数与基本参数之间存在近似的线性相关性，而导致法方程病态，严重影响计算结果的稳定性。同样，在GPS载波相位测量和地球重力场计算中也会存在类似的现象。针对法方程病态问题，利用正则化方法，通过选择合适的正则化参数和正则化矩阵，可有效地削弱法方程的病态性，增强解的稳定性。而传统的正则化方法，没有考虑观测值含有粗差的情况，当观测值含有粗差时，传统的正则化方法无法消除或削弱含有粗差的观测值对平差结果的影响，同样会导致平差结果失真。为此，文献[5-6]中提出具有抗差性的病态问题平差方法，即通过方差膨胀模型降低含有粗差的观测值的权，以削弱粗差观测值对平差结果的影响。

所有的方差膨胀模型都是通过观测值的残差建立起来的，即通过观测值的残差确定观测值的权。但是，已知的病态问题抗差方法中，计算出的残差均是有偏的，而使用有偏的残差建立方差膨胀模型显然是不合理的。因此，对残差进行有偏性改正，建立有偏改正的方差膨胀模型，而所有的不适定问题解的表达都可以由Tikonov正则化原理导出，本文结合有偏改正的方差膨胀模型和正则化原理，提出了一种新的正则化抗差方法，即有偏改正的正则化抗差方法。

1 正则化抗差方法

设病态问题的观测方程为

L=AX+Δ.

(1)

根据Tihonov正则化原理，得估计准则为

(2)

根据式(2)的估计准则，若观测值中含有粗差，参数估值将受到严重影响，即式(2)中的估计准则不具备抗差性，文献[6]提出了一种具有抗差性的估计准则：

(3)

式中：n为观测值个数，Pi为第i个观测值的权，ρ为任意选取的抗差迭代函数，Vi为平差后第i个观测值的残差。

由式(3)中的估计准则，可得参数的估值：

(4)

由式(4)可以发现，等价权矩阵的确定与残差V紧密相关，残差V能否有效的将直接影响平差结果的质量。利用正则化方法估计的参数是有偏的，根据有偏的参数计算得到的残差必然也是有偏的，那么，利用有偏的残差进行等价权矩阵的计算显然不合理的。

2 有偏改正的正则化抗差方法

2.1 残差V有偏性分析

根据式(3)和式(4)得残差V的计算式为

(5)

(6)

其中

E(V)不等于0是由两个原因造成的，一个原因是正则化参数α和正则化矩阵R引起的；另一个原因是Δ中含有粗差引起的。但此处可不考虑粗差的影响，而只考虑由正则化参数α和正则化矩阵R对残差V的有偏性的影响。粗差对V的影响，可通过之后的选权迭代法来处理，以降低相应观测值的权。

不考虑粗差的影响，对V求期望得

(7)

(8)

(9)

由式(9)可得残差V的一次有偏量和二次有偏量为

(10)

对式(9)继续使用上述的推导方法，可得V的更高次的有偏量。需要指出的是，通过计算分析，对V进行二次有偏量的改正，明显改善解的稳定性。

残差V的有偏改正结果为

(11)

2.2 有偏改正的正则化抗差模型

有偏改正的正则化抗差准则为

(12)

对X求导，并令其等于零可得

(13)

式中：Ai为系数阵A的第i行元素。

成等价权的形式：

(14)

其中

矩阵形式可得

(15)

有偏改正的正则化解为

(16)

有偏改正的正则化抗差方法与普通的正则化抗差方法，在解的表达形式上基本一致，不同的是，将式(4)中的等价权阵换成了式(16)中的等价权阵。式(16)中等价权阵的确定在理论上更加严密，推导过程更加严谨。

3 算例分析

本文取历元间隔为2 s，观测了5颗卫星，用4个历元解算整周模糊度，误差方程系数阵为

(17)

设参数的真值为

(18)

式中：Ni为整周模糊度参数，δx，δy，δz为坐标参数。

表1 模拟值

本文采用4种估计方法对实例进行估计分析，4种估计方法分别为最小二乘估计(LS)，正则化估计，正则化抗差估计，有偏改正的正则化抗差估计。其中，3种正则化方法中正则化参数α和正则化矩阵R的选取通过L-curve方法、GCV方法，截断奇异值方法均无法取得良好的效果。根据单频GPS观测值的特点，本文3种正则化估计方法中正则化参数α和正则化矩阵R的选取使用MINE Ι方案；两种抗差估计方法中ρ函数的选取使用IGG方案。

当观测值中不含有粗差时，即直接利用表1中的Li行对应的观测值，使用4种方案进行平差，获得的参数估值，参数估值的均方误差，以及已知的参数真值分别列于表2中。当观测值中含有粗差时(本文在表1中Li行对应的观测值中给第1个观测值增加了-0.15的粗差，给第2个观测值增加了0.25的粗差)，获得的参数估值，参数估值的均方误差，以及参数的真值分别列于表3中。

由表3的计算结果可知，当观测值中不存在粗差时，3种正则化方法的结果几乎没有任何差异，但在均方误差意义下远远好于最小二乘估计方法(LS)。当观测值中含有粗差时，最小二乘估计方法(LS)的平差结果是灾难性的；正则化估计方法和正则化抗差估计方法，在均方误差意义下均受到粗差观测值的明显影响，但是正则化抗差估计方法相对于正则化估计方法受到粗差观测值的影响较小。而本文提出的正则化抗差方法，在均方误差意义下，几乎不受粗差观测值的影响，明显优于另外3种估计方法。并且，通过多次实验，有偏改正的正则化方法均能保证平差结果的稳定性，可以较好地消除粗差观测值的影响。

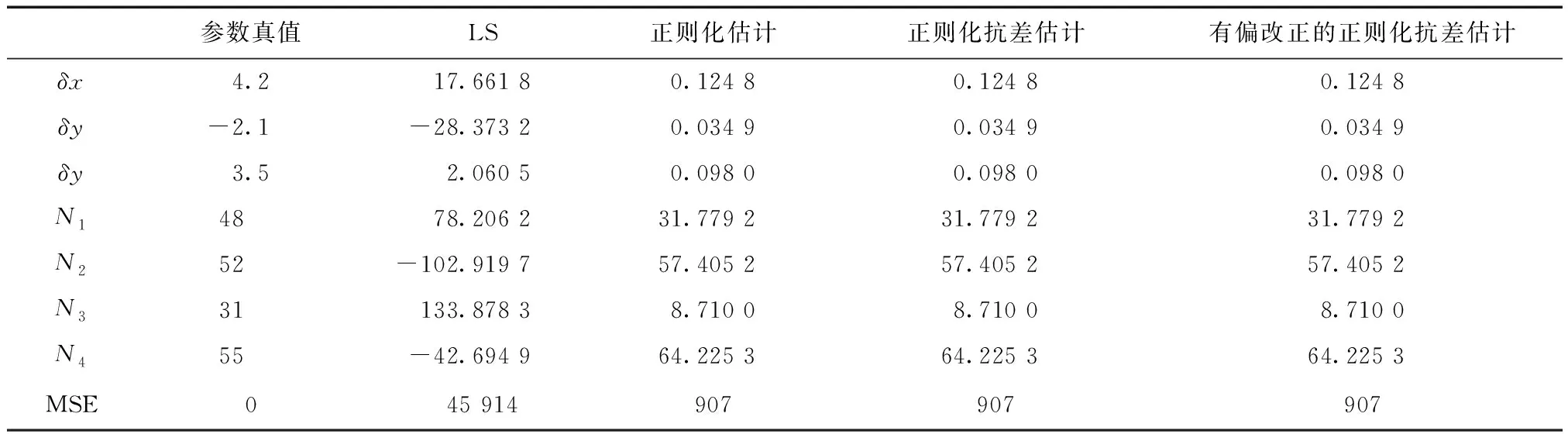
表2 观测值不含粗差的平差结果

表3 观测值含有粗差的平差结果

4 结束语